题意：Gildong有一个n个数字的数组a。支持两种操作：1.给一个后缀每个数字增加1
2.给一个后缀每个数字减去1 你可以修改一个数字或者选择不修改，求这个数组每个数字变成一个相等数最少的修改次数。
分析：我们假设最终得到的数字为\(b\)。
我们考虑如下的四个数字
\(a_{1}, a_{2}, a_{3}, a_{4}\)
首先是\(a_{1}\)变成b，那么所需要的次数为\(abs(b - a_{1})\)，得到
\(b, a_{2} + b - a_{1}, a_{3} + b - a_{1}, a_{4} + b - a_{1}\)，
然后我们把\(a_{2} + b - a_{1}\)变成b，所需要的次数为\(abs(b - (a_{2} + b - a_{1})) = abs(a_{1} - a_{2})\)，得到
\(b, b, a_{3} + b - a_{1} + b - (a_{2} + b - a_{1}), a_{4} + b - a_{1} + b - (a_{2} + b - a_{1})\)
化简为
\(b, b, b + a_{3} - a_{2}, b + a_{4} - a_{2}\)
然后我们把\(b + a_{3} - a_{2}\)变成b，所需要次数为\(abs(b - (b + a_{3} - a_{2})) = abs(a_{2} - a_{3})\)得到
\(b, b, b, b + a_{4} - a_{2} + b - (b + a_{3} - a_{2})\) = \(b, b, b, b + a_{4} - a_{3}\)
然后我们最后只需要\(abs(a_{3} - a_{4})\)，即可把整个数组变成b。
总共的次数为\(b + abs(b - a_{1}) + abs(a_{1} - a_{2}) + abs(a_{2} - a_{3}) + abs(a_{3} - a_{4})\)，
当b为\(a_{1}\)时，前面的项可以消掉，变成0，即\(abs(a_{1} - a_{2}) + abs(a_{2} - a_{3}) + abs(a_{3} - a_{4})\)。
观察这个式子，我们修改一个数可以像\(a_{2}\)一样，影响两个式子，也可以像\(a_{1}\)和\(a_{4}\)一样，影响一个式子，
所以，当我们修改一个数的时候，对于像\(abs(a_{1} - a_{2}) + abs(a_{2} - a_{3})\)这样的式子，我们化简，为
\(y = abs(c1 - x) + abs(x - c2)\)，\(x\)是我们需要修改的数，我们应该让这个式子尽量小，这是一个绝对值函数，
函数图像如下：这是\(f(x)=abs(3-x)+abs(x-5)\)的图像，当x为[3, 5]之间的时候，取到最小值，我们只需要分类讨论下即可，
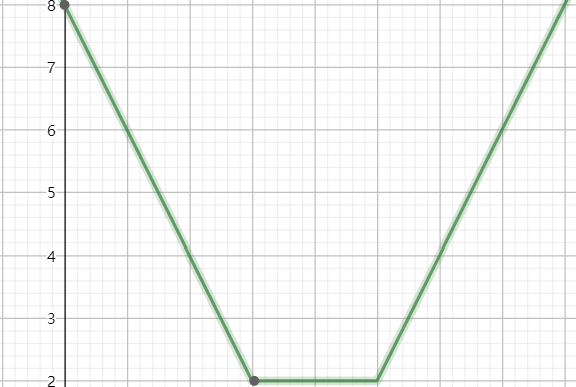
因此，我们只需要对每一项做差，查看差值的大小，然后就可以求得答案。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 200005;
typedef long long ll;
ll a[N];
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
//vector<int> v;
ll mx = 0;
ll sum = 0;
for(int i = 2; i < n; ++i)
{
ll tmp = 0;
if(a[i - 1] > 0 && a[i + 1] > 0)
{
tmp = abs(a[i - 1] - a[i + 1]);
}
else if(a[i - 1] < 0 && a[i + 1] > 0)
{
tmp = abs(a[i - 1]) + abs(a[i + 1]);
}
else if(a[i - 1] > 0 && a[i + 1] < 0)
{
tmp = abs(a[i - 1]) + abs(a[i + 1]);
}
else if(a[i - 1] < 0 && a[i + 1] < 0)
{
tmp = abs(a[i - 1] - a[i + 1]);
}
else
{
tmp = abs(a[i - 1]) + abs(a[i + 1]);
}
ll now = abs(a[i - 1] - a[i]) + abs(a[i] - a[i + 1]);
//cout << tmp - now << "***" << endl;
mx = min(mx, tmp - now);
//v.push_back(abs(abs(a[i + 1] + a[i - 1]) - a[i]));
}
mx = min(mx, -abs(a[1] - a[2]));
mx = min(mx, -abs(a[n - 1] - a[n]));
//cout << mx << "---" << endl;
for(int i = 1; i < n; ++i)
{
//cout << a[i] << "-" << a[i + 1] << endl;
sum += abs(a[i] - a[i + 1]);
}
printf("%lld\n", sum + mx);
}
return 0;
}
