UPC GCPC2019 K: Move & Meet

题意:两个人在一个无限的棋盘上玩.每个人都有个初始位置,它们都要走特定的步数.求可以走到的相同位置.如果不存在这个位置,则输出"impossible".

输入:给定两行\(x, y(-10^{12} <= x, y <= 10^{12})和d(0 <= d <= 10^{12})\).d表示要走的特定步数.

分析:先交换y1, y2(如果y1 < y2),这样y1就在y2上面,那么我们的x1和x2就只存在两种情况,x1 < x2或者x1 > x2,我们只需要判断这两种情况即可.

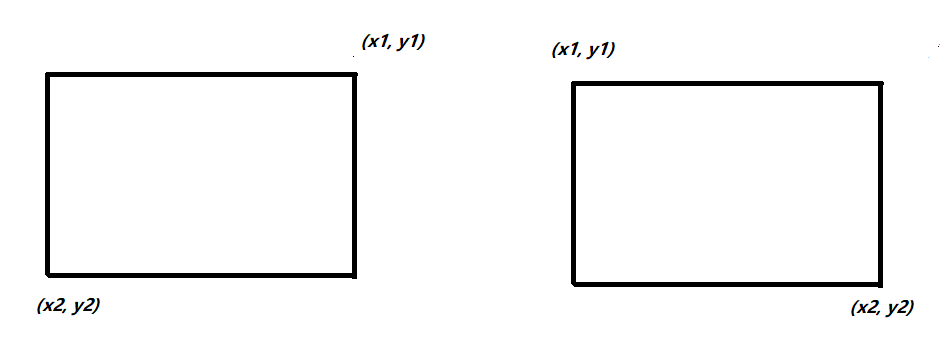
首先是求出两个点之间的曼哈顿距离,即dist = abs(x1 - x2) + abs(y1 - y2),然后比较d1 + d2和dist的大小,如果dist > d1 + d2,说明不存在合法的点使得两个人走在一起,其次是如果d1 + d2 - dist多出来的步伐是一个玩家要左右横跳的次数,这个次数要% 2 == 0.然后我们需要找出能够到达的合法的点,对于c = d1 + d2 - dist,这个c我们要消耗掉,让两个玩家分担,需要注意的是,分担的时候必须偶数偶数的分担,这样才能反复横跳.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;
using ll = long long;
int main()
{

        ll x1, y1, d1, x2, y2, d2;
        int t;
        while (cin >> x1 >> y1 >> d1 >> x2 >> y2 >> d2)
        {
            ll dist = abs(x1 - x2) + abs(y1 - y2);

            ll c = (d1 + d2) - dist;

            if (c < 0 || c % 2)
                puts("impossible");
            else
            {
                if (y1 < y2)
                {
                    swap(x1, x2);
                    swap(y1, y2);
                    swap(d1, d2);
                }
                if (x1 <= x2 && y1 >= y2)
                {
                    ll q = min(d1, c);
                    if (q == d1)
                    {
                        if (d1 & 1) d1 = 1;
                        else d1 = 0;
                        d2 = d2 - (c - d1);
                    }
                    else d1 = d1 - c;
                    ll dist = abs(x2 - x1);
                    ll q2 = min(dist, d1);
                    if (q2 == d1) cout << x1 + d1 << " " << y1 << endl;
                    else cout << x2 << " " << y1 - (d1 - dist) << endl;
                }
                else if (x1 >= x2 && y1 >= y2)
                {
                    ll q = min(d1, c);
                    if (q == d1)
                    {
                        if (d1 & 1) d1 = 1;
                        else d1 = 0;
                        d2 = d2 - (c - d1);
                    }
                    else d1 = d1 - c;
                    ll dist = abs(x2 - x1);
                    ll q2 = min(dist, d1);
                    if (q2 == d1) cout << x1 - d1 << " " << y1 << endl;
                    else cout << x2 << " " << y1 - (d1 - dist) << endl;
                }
            }
        }        
    return 0;
}