纹理映射浅述
写在前面:
本文章为个人学习笔记,方便以后自己复习,也希望能帮助到他人。
由于本人水平有限难免出现错误,还请评论区指出,多多指教。
部分图元和素材来源于网络,如有侵权请联系本人删除。
参考资料与链接会在文章末尾贴出。
=======================================================================
1.纹理映射(Texture Mapping)
考虑下图这样两种情况:
1)场景中的小球被两个台灯(可视为两个点光源)所照亮,按照Blinn-Phong光照着色无非就是两个点光源的贡献加起来。特别之处在于球面上有三个不同区域,蓝色,黄色,红色星星,按照图中公式就是这三个区域的k_d(漫反射系数)不同但是光照模型是相同的。
2)场景中的地板纹路跟小球也是应用一样的光照模型,然而每一个点上漫反射系数差别却很大,如果要我们在程序去手动定义每个点的漫反射系数显然是不现实的。于是乎我们希望有这么一种方法能够定义模型上每个点的属性(不只是漫反射系数)。
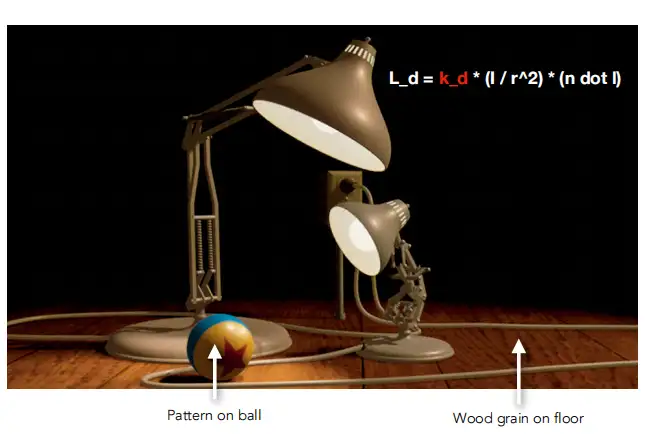
那么该如何定义物体表面的属性呢?
首先我们这样去理解,任何三维物体表面都是二维的,我们可以将三维物体表面上的任意一点映射到二维平面上去。
比如地球仪,如果将其剪开再展开不就成为了一张二维的世界地图了嘛?
如果我们拥有三维物体表面的任意一点和二维纹理上某一点的映射,也就是说拥有不同坐标空间下的映射关系,我们就可以把物体表面上的属性存到二维纹理中,待到需要的时候通过对应的坐标查询该点的属性(漫反射系数,法线等)进行后续计算即可,这就是纹理映射。

我们来看下下图的例子,最左边是我们通过Blinn-Phong得到的光照模型计算结果,而右边就是加上纹理后的渲染结果。可以看到细节增加非常多,表现力比之前更加突出。
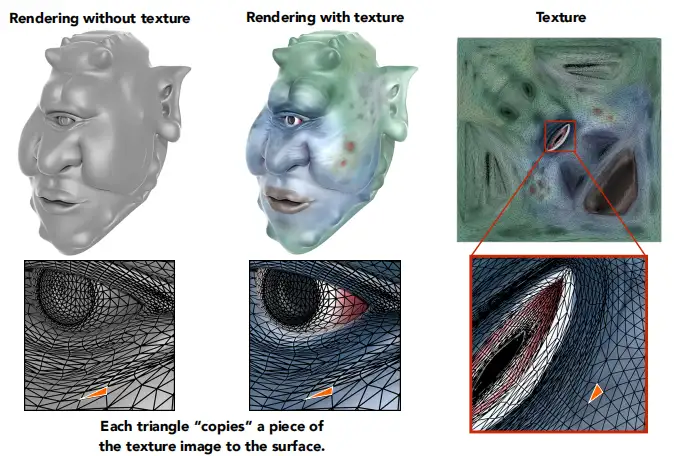
这里还涉及的知识点就是物体表面与纹理之间如何映射(当然不是把纹理简单“贴”上去这么简单),不同形状的物体(如平板,球体,圆柱,不规则形状等)该如何将其表面“展开”到二维纹理而又尽量少扭曲呢?这里又是一个更深奥的知识——参数化。目前我们就默认有艺术家和工程师用某些软件已经帮我们展开了。
有的时候一张纹理并不足以覆盖整个物体或场景,这时我们可以用同一张贴图重复“贴”在同一物体上。

虽然在uv坐标可视化下会非常突兀,但在正常纹理下却是十分自然的。这归功于一种叫tiled的纹理,由艺术家精心设计过即便重复拼接后也是四周连续的,一般用作为墙面和地面的贴图纹理。

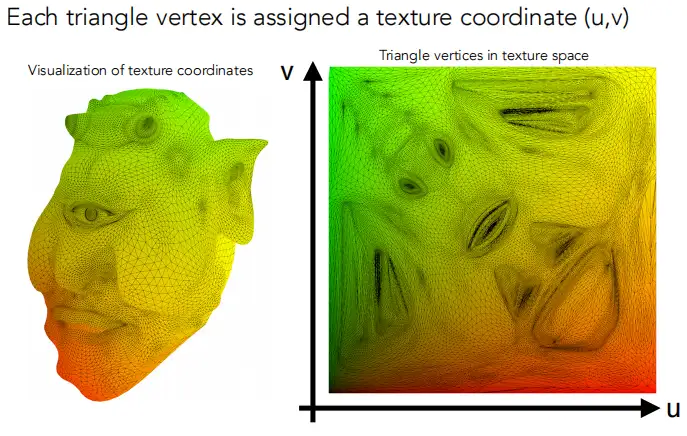
对于纹理空间坐标我们一般用uv表示,在纹理空间之内任意一个二维坐标都在[0,1]之内。
为什么整幅纹理可视化之后是红色和绿色呢?可以将(u,v)坐标的两点想象成RGBA的red和green通道就能明白了。一幅Texture上的任意一点都可以用一个(u,v)坐标来表示(0<=u<=1,0<=v<=1),因此只需要在三维world space中每个顶点的信息之中存储下该顶点在texture space的(u,v)坐标信息,自然而然的就直接的得到了这种映射关系。
下面给出纹理采样的伪代码:

2.纹理问题
2.1纹理分辨率过小引发的问题
在理想情况下我们制作一张1000x1000的纹理贴图希望应用在1000x1000分辨率的屏幕上,但实际应用情况是,几乎不会有这么巧合与完美的情况。试想现在我们制作了一张100x100的纹理贴图应用在1000x1000分辨率的屏幕上势必会造成模糊不清的情况,因为屏幕几个相邻的采样点采样的都是纹理贴图上的同一个纹素(texel),这就会造成所谓的“走样”(aliasing)现象。如下图:
图中红点我们看成屏幕的一个像素的采样点与其在纹理空间中所对应的位置,黑点是贴图采样点,最终采样会选择离红点最近的一个黑点,也就是橙色框起来的那个黑点。显然如果多个采样点落到此范围内就会采样同一个点,最后屏幕几个像素点显示同一个纹理贴图上的值。
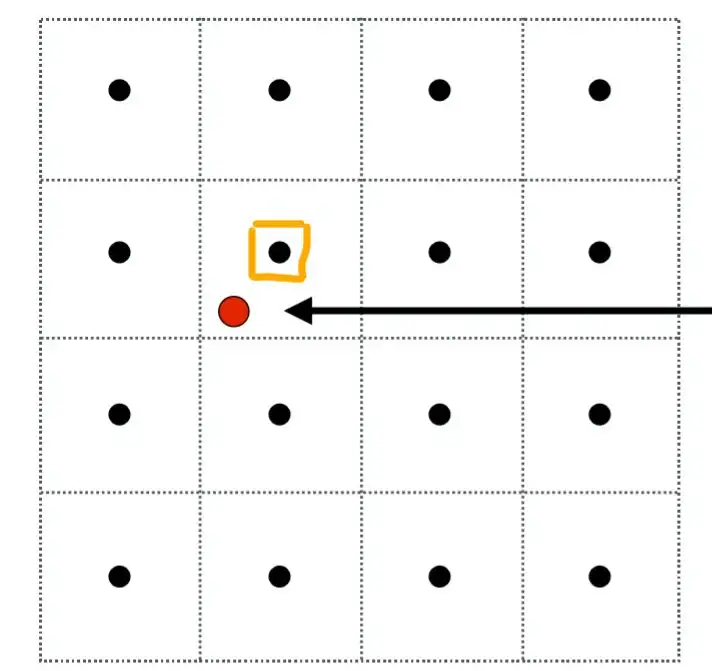
我们可以用双线性插值(Bilinear Interpolation)来缓解纹理分辨率不足引发的走样问题。
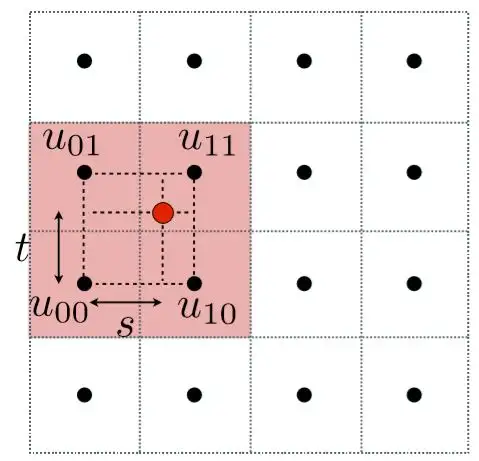
如图,首先我们会选择离红色点最近的四个黑点,且分别计算出红点在水平和竖直方向上的“偏移值”,记为S和T。
第二步,我们利用下面给出的插值公式,以s为权重计算出水平方向上u0和u1两个黑点的值

最后,再用插值公式以t为权重计算出竖直方向上红点的颜色值。
如此一来,我们考虑到了采样点周围最近四个点的颜色值,利用两次线性插值计算能不错地缓解纹理分辨率不足带来的走样问题。

Bicubic则是一种能获取更优秀画面表现的方法,只不过相应地,计算量也会更大一点。
2.2纹理分辨率过大引发的问题
既然纹理分辨率过小会引发模糊之类的问题,那只要把纹理分辨率做大就可以了吧?事实上除了要考虑纹理过大(或者说高分辨率纹理)对内存等造成的压力,其本身的渲染在某些情况下也是会出现走样问题的甚至比纹理分辨率过小的问题更加棘手,如下例子所示:
想象我们将正方形格子铺满在地板上,这是我们所期望的结果
然后当我们用上文提到的采样贴图公式来计算所得到的的结果确实这样子的,远处出现摩尔纹,近处出现锯齿。
那为什么会导致这样的问题呢?
我们观察此纹理,其中都是同样大小的方格,但是近大远小,同样是4个方格大小的区域,在近处可能在屏幕空间中占到100个像素的大小,但是到了远处时可能在屏幕空间中仅仅占有几个像素大小。回想上文的纹理采样,理想状态下我们想用屏幕中一个像素采样点去采样贴图中的一个像素点,而现在情况则是试图用屏幕中一个采样点去采样纹理贴图中的一个范围内的点,也就是想让一个点的采样结果代表整个范围内所有点的颜色信息。(从信号与系统这门课的知识来讲就是,采样频率过低无法还原信号原貌)。
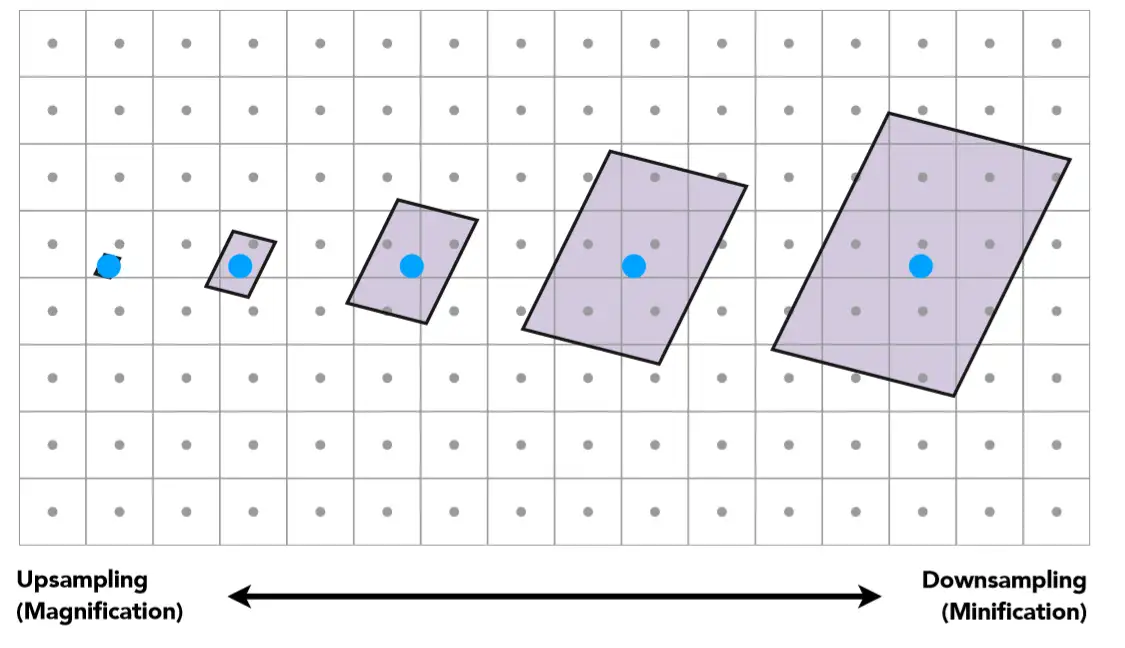
如上图所示,如屏幕空间中的蓝色采样点离我们(摄像机)越远,其“采样”的范围就越大,范围内的像素点越多,我们把该范围称之为屏幕像素在纹理空间的“footprint”。图中越右边就是越欠采样,有人想到既然一个像素点采样过少,不能代表该范围的颜色信息,那我们是不是可以把该像素细分为更多的采样点,该方法叫做SuperSampling。

如上图所示,所计算结果确实好了不少,但是付出的代价同样巨大!因为原来的一个像素点被分为了512个采样点,计算量简单算下来是原来数百倍。这只是一个像素点,如果是一块1920x1080的屏幕呢?如果是footprint更大包含更多纹素需要我们细分成更多采样点呢?这显然是不够合理的在实际应用开发中。
于是我们开始找寻其他办法。
2.1.1 Mipmap

回顾这张图,我们一直都想用屏幕上的采样点去采样纹理中的某个“点”从而计算结果,是一种点对点的查询;如果我们能计算出一个值,这个值能代表footprint内的所有纹素的值呢?这样我们就变成了点对区域的查询,即Point Query变为Range Query。

如上图所示,不同的footprint中所包含的纹素数量也是不同的,显然近处右下角的footprint所包含的纹素比远处墙壁的纹素要少。因此我们需要把footprint分开成不同的级别以适应不同的情况,这就是Mipmap所做的事情。

如上图,level0代表了原始纹理,而level1则将纹理分辨率降了一半,level2继续将上一级别分辨率降低直至最高level纹理分辨率变成1x1。每提升一级将4个相邻的像素点合并求均值为一个像素点,直白地讲越高级别的mipmap实际上代表了更大范围footprint的区域查询值。然后我们只需要根据不同的footprint大小来选择不同level的mipmap进行查询。
那么我们如何确定footprint对应的mipmap level呢?
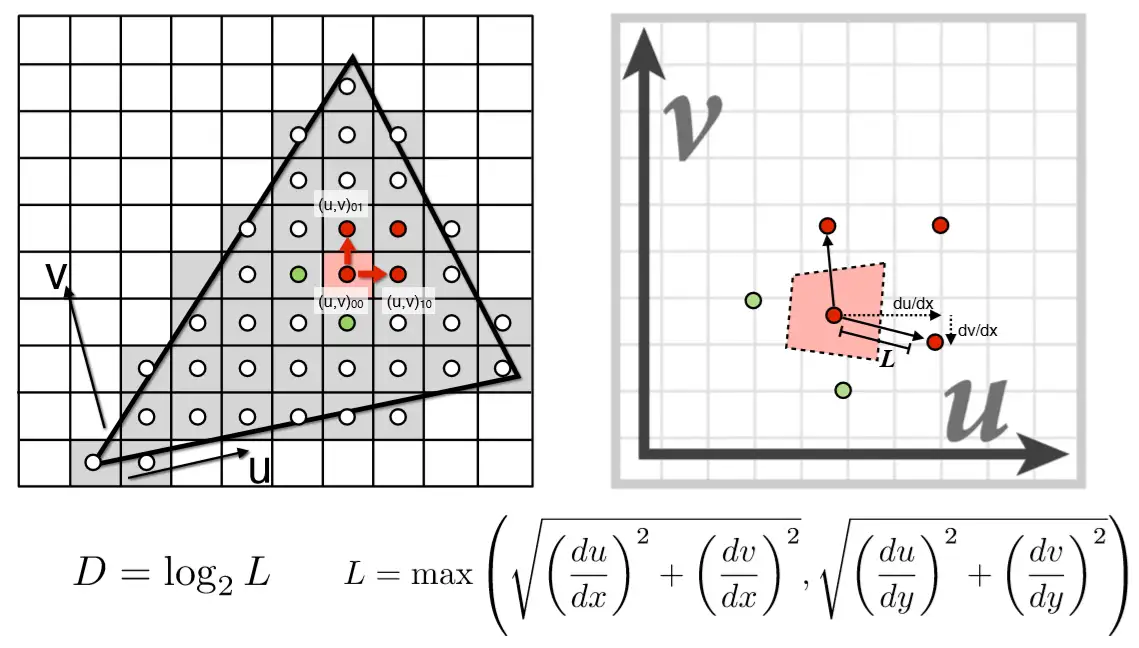
简单来说就是把屏幕的像素点“投影”到纹理贴图的对应位置,试图计算出屏幕空间下相邻像素点所形成的微小空间对应到纹理贴图上是多大的范围(与微分定义相似)。如上图例子所示,假如我们想求00点,我们需要去上面和右边两个点在纹理贴图中对应位置做计算(右边公式已给出),然后二者取其大作为L,再用其做对数运算即可算出D值,我们把D四舍五入作为应选择的level可得到下面结果:

如此一来我们得到了想要的结果,根据footprint选择mipmap,但实际上我们观察发现,两个level之间的mipmap变化十分突兀,因此,为了追求平滑过渡的结果,我们可以在level与level之间再做一次插值。比如我想要1.8级的结果,那我们就可以查询level1和level2的结果,再做一次插值,结果如下:
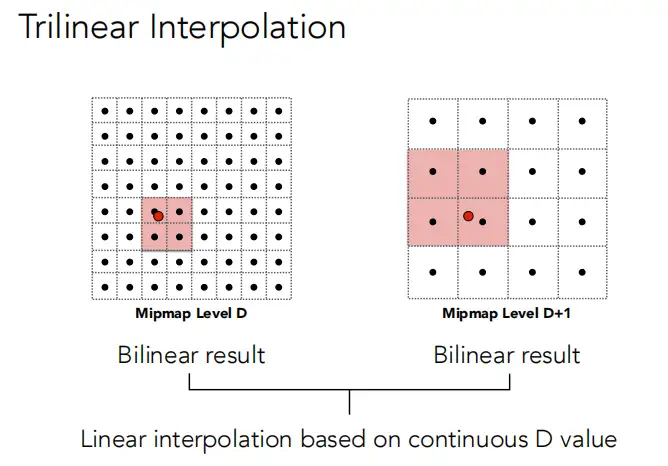

那是否如此应用了mipmap就能获得我们理想的结果了呢?并不尽然,mipmap也有它的局限性,我们先看看mipmap应用的效果:
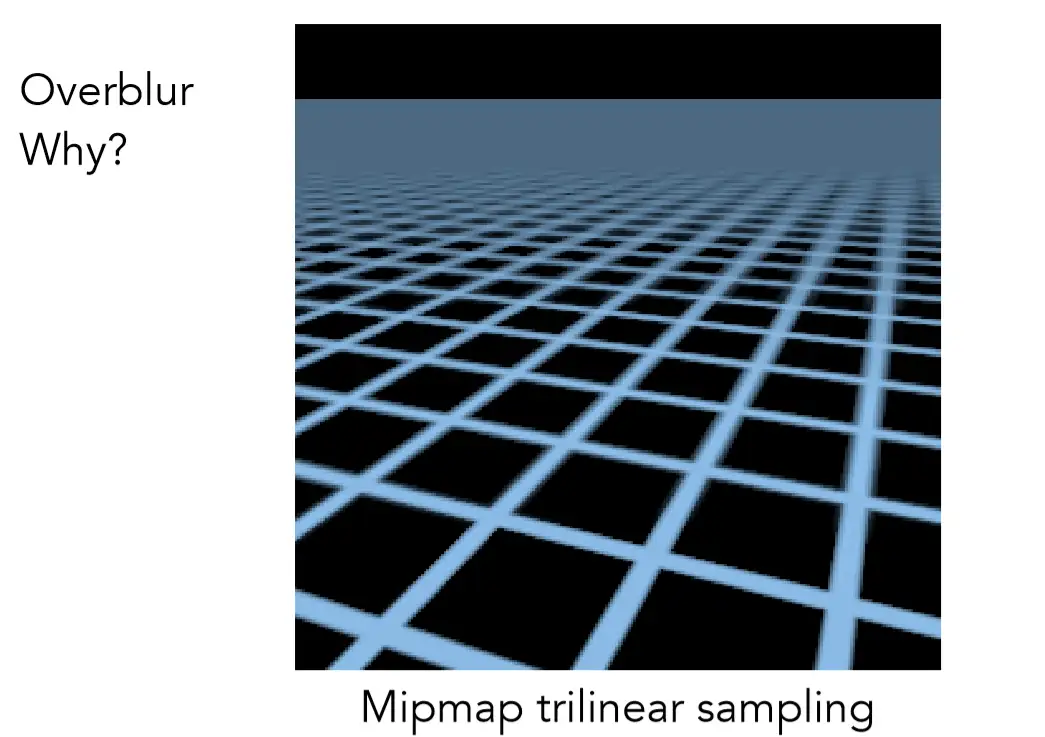
我们可以看到远处出现了Overblur的现象,为什么会这样呢?mipmap是一种快速的,近似的,应用于正方形的一种查询方法。那如果footprint是不规则的形状呢?那么mipmap的近似准确性就会大大下降。在实际应用中会有除了正方形区域外的各种形状。
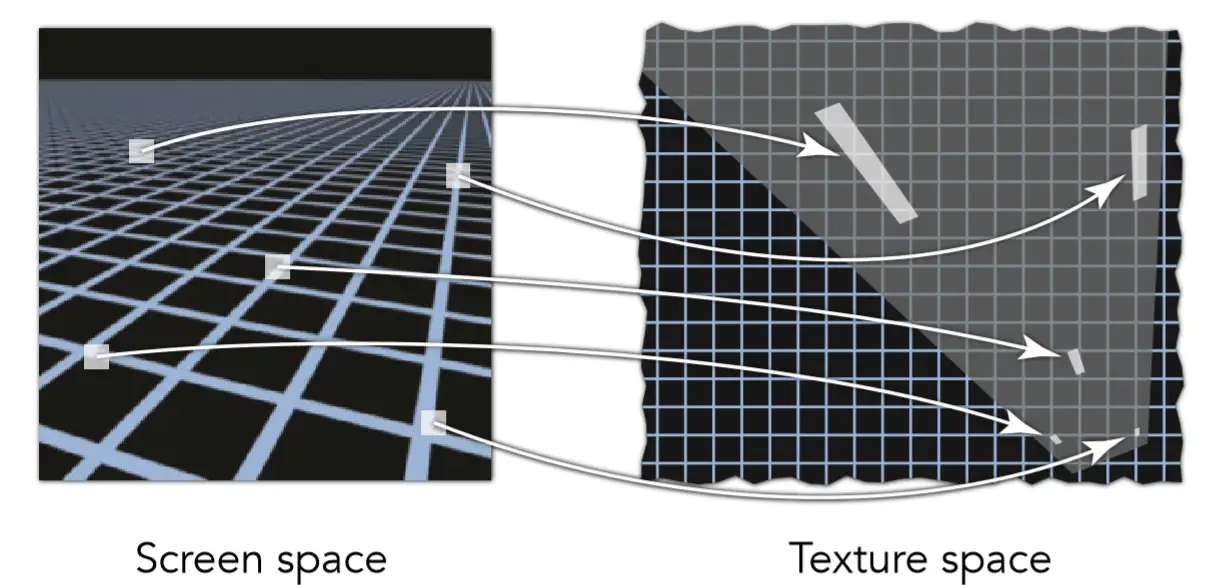
2.1.2各向异性过滤(Anisotropic Filtering)
因此,一种叫各向异性过滤的方法便用于解决mipmap的部分问题。简单来说,各向异性过滤还考虑了单竖直和水平方向上的不同level,应用于长条矩形的footprint情况,而mipmap可以看做仅仅计算了了下图中对角线的纹理。


可以看到远处情况比mipmap表现得好一些。但是其仍然有不足之处,那就是没有解决对角线(diagonal)的footprint,因为各向异性过滤也只是计算了水平和竖直方向的footprint。
要想处理diagonal footprint还需要其他的方法。
参考资料:
1.现代计算机图形学入门–闫令琪
2.Fundamentals of Computer Graphics,Fourth Edition




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· 单线程的Redis速度为什么快?