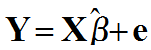多元线性回归的预测
回归模型除了对参数进行估计和检验,以弄清楚变量的相关性和因果性之外,另一个目的便是进行预测。
那么,由OLS方法的出来的预测结果是否可靠呢?预测结果的可靠性又会受什么因素的影响呢?除了点估计的预测结果,能否有区间估计的预测结果呢?
本文就这些问题,来进行一一探讨
1.引入why?
回归模型除了对参数进行估计和检验,以弄清楚变量的相关性和因果性之外,另一个目的便是进行预测。
那么,由OLS方法的出来的预测结果是否可靠呢?预测结果的可靠性又会受什么因素的影响呢?除了点估计的预测结果,能否有区间估计的预测结果呢?
本文就这些问题,来进行一一探讨
2.问题具体是什么?what
首先,说明初始的多元线性估计模型:
在多元线性估计的过程中,我们已经得出了线性模型的估计形式
那么,现在我们有了模型形式以及参数的估计值。在被给定另一组自变量样本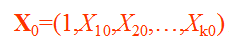 的条件下。
的条件下。
需要注意的是,上式只是对Y预测值的估计,并非对Y的估计。因为由公式(1)看出,Y是由两部分组成的,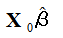 只是
只是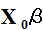 的估计,模型的随机项
的估计,模型的随机项 是无法估计的。所以我们说(3)式只是对Y的预测值的估计。
是无法估计的。所以我们说(3)式只是对Y的预测值的估计。
那么现在问题来了,我们现在求得的只是一个预测值的估计,那么Y的预测值E(Y0 )的区间估计能否得出,进一步Y0 的估计区间又能不能得出呢?
什么?为什么要进行区间估计?很简单,因为只有点估计的话,你根本不知道点估计靠不靠谱,如果告诉你你下次考试预计分数是95,以及90-100这个分数区间包含你下次考试的分数的概率为90%,你觉得那种说法更靠谱呢?
3.解决思路
构造统计量,该统计量要分别包括E(Y0 )
对于E(Y0 )的区间估计:
易知:

则可以通过y(hat)服从正态分布,但是方差未知,明显,可以用样本方差来进行t统计量的构建
对于Y0 的区间估计
 服从正态分布,我们是知道的,而
服从正态分布,我们是知道的,而 的分布也是有假设的,那么e0 的分布状况也就能够轻松获得了
的分布也是有假设的,那么e0 的分布状况也就能够轻松获得了
4.解决过程
对于 的区间估计
的区间估计

对于 的区间估计
的区间估计


注:t分布是由正态分布推导出来的。
其中,e为样本标准差。
总结
从

可以看出
- x0越与估计样本x差异大,区间也就越大,估计也就越不精准,这就是为什么回归模型不适合外推
- x的共线性越大,
 也就越小,从而
也就越小,从而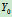 的估计区间也就越大,估计越不精准。
的估计区间也就越大,估计越不精准。