数据结构与算法(六):队列
队列和栈一样,也是一种对数据的存和取有严格要求的线性存储结构。
与栈结构不同的是,队列的两端都"开口",要求数据只能从一端进,从另一端出
什么是队列?
队列的定义
队列(queue)是一种采用先进先出(FIFO)策略的抽象数据结构,即最先进队列的数据元素,同样要最先出队列
如下图所示:
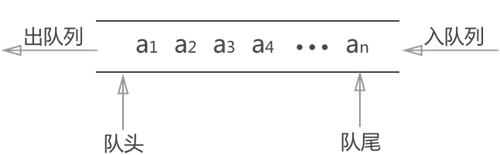
队列的相关概念
- 对头和队尾:队头指向的是第一个元素,而队尾指向的是最后一个元素
- 入队(enqueue)操作:入队操作就是将一个元素添加到队尾
- 出队(dequeue)操作 :出队操作就是从队头取出一个元素
队列实现
队列和栈一样可以由数组实现顺序队列也可以由链表实现链式队列,由于数据和链表数据结构的不同,其生成的队列也会有相应的区别。不过不必过于纠结这些,我们知道队列怎么用?以及如何用队列解决实际问题即可。
顺序队列
不管使用那种方式来实现队列,都需要定义两个指针分别指向队头和队尾,本文中我们用head指向队头,tail指向队尾,后面的示例中这将默认使用这个,有特殊的地方会进行说明,先来看看顺序队列的入队、出队操作。
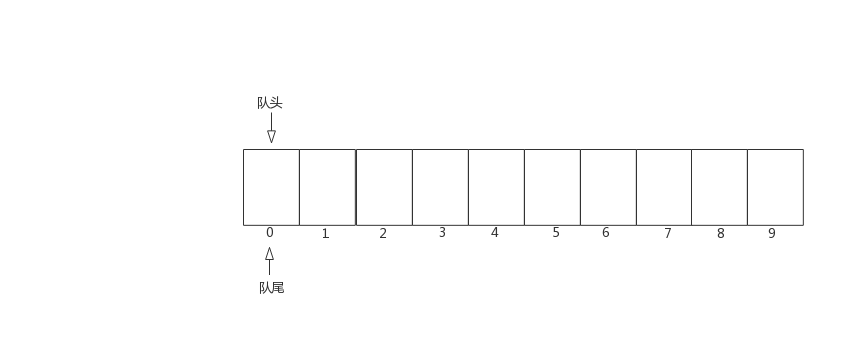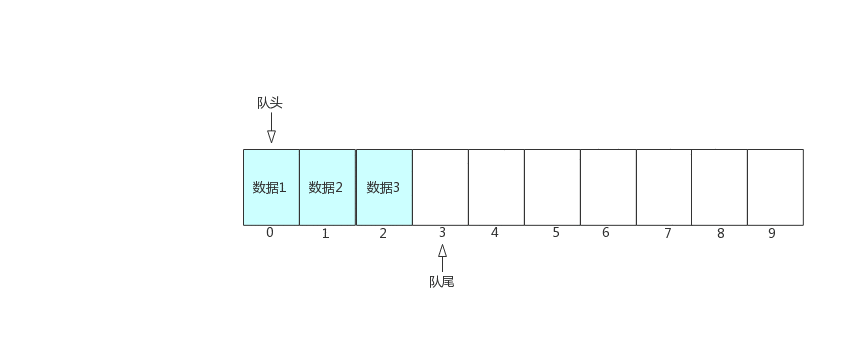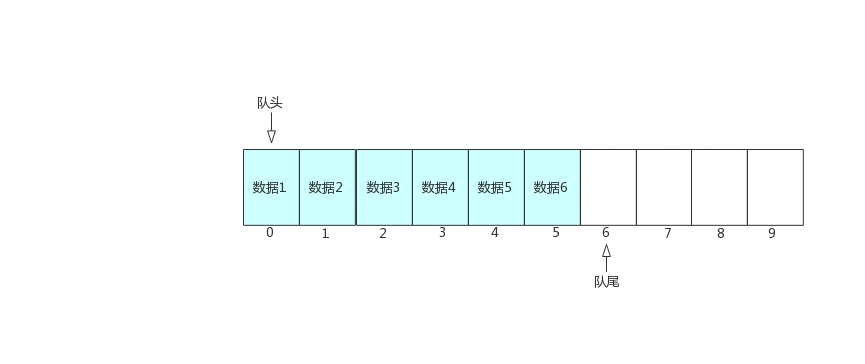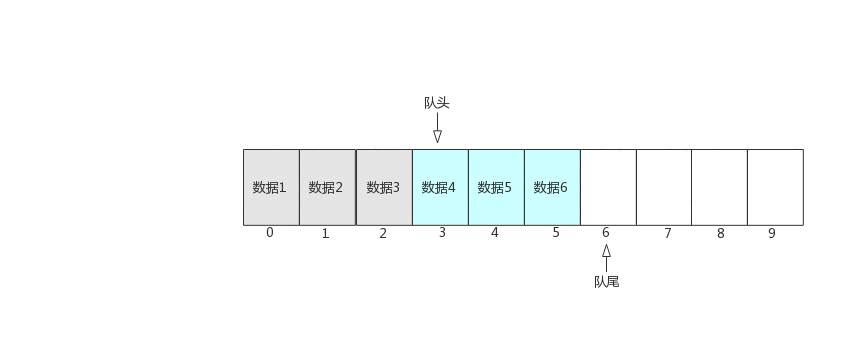
图中可以看出,入队时,队尾往后移动,队头保持不变,出队是队头往后移动,队尾保持不变。
入队、出队操作的逻辑都比较简单,可能你有疑问的地方是:
出队时为什么队头要往后移动而不是一直指向数组下标为0的位置? 为什么呢?
如果我们保持队头一直指向数组下标为0的位置,那每次出队操作后,后面的数据都需要往前挪一位,换句话说每次出队操作都需要进行数据迁移,而数据迁移的代价比较大,每次数据迁移的时间复杂度为O(n),这样会极大的影响队列的使用性能。如果我们出队时,队头往后移动一位,这样我们就避免每次出队都进行数据迁移,我们只需要在只有在tail等于数组大小且head不等于0时,进行一次数据迁移,将已经出队留下的空间继续供入队时使用。数据迁移时,从head位置开始的数据都需要往前移动head位,这样就把出队后的空间腾出来,供后续入队操作使用。
下图是数据迁移的过程:
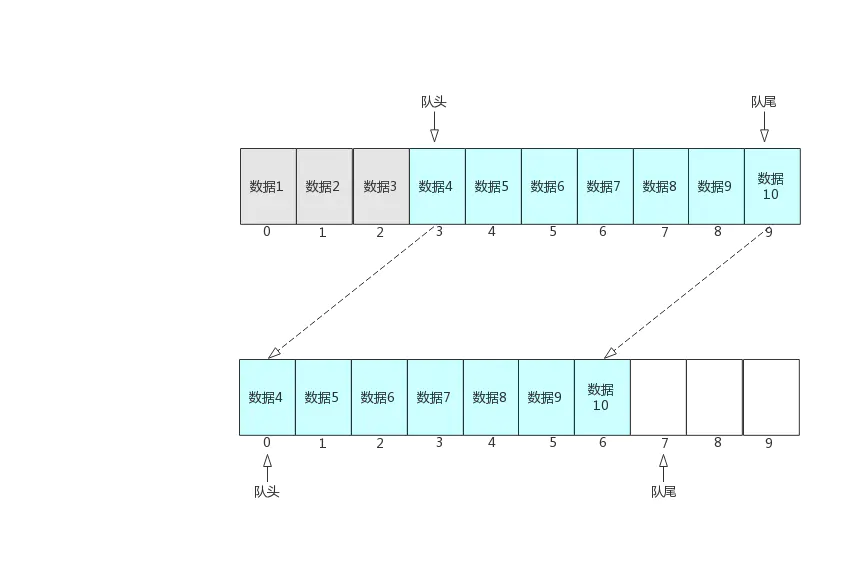
代码如下:
/**
* 基于数组的顺序队列
*/
public class ArrayQueue<T> {
/**
* 存放数据的数组
*/
private T[] items;
/**
* 容器大小
*/
private int size = 0;
/**
* 头指针:指向队列的第一个元素
*/
private int head = 0;
/**
* 尾指针:指向队列的最后一个元素
*/
private int tail = 0;
/**
* 构造函数
*
* @param size 初始化容器大小
*/
public ArrayQueue(int size) {
this.size = size;
items = (T[]) new Object[size];
}
/**
* 入队操作
*
* @param data 添加元素
* @return true:入队成功;false:入队失败
*/
public boolean add(T data) {
// 判断队列满了的条件,tail = size,head = 0
if (tail == size && head == 0) {
return false;
}
// 如果tail = size,但是head != 0,说明前有数据删除,队列未满,需要数据迁移
if (tail == size) {
// head 后面的数据都需要往前迁移 head 位
for (int i = head; i < size; i++) {
items[i - head] = items[i];
}
// 将尾指针向前移动 head 位
tail -= head;
// 将头指针指向 0 位
head = 0;
}
// 向队列中添加元素
items[tail++] = data;
return true;
}
/**
* 出队操作
*
* @return
*/
public T get() {
// 第一个元素和最后一个元素相等时,队列为空
if (head == tail) {
return null;
}
// 头指针向后移动一位,这样做的好处是在出队时不需要数据迁移
T result = items[head++];
return result;
}
}
链式队列
链式队列实现起来相对顺序队列来说要简单很多,我们先来看看链式队列的入队、出队操作:
从图中可以看出链式队列入队操作是将tail的next指向新增的节点,然后将tail指向新增的节点,出队操作时,将head节点指向head.next节点。链式队列与顺序队列比起来不需要进行数据的迁移,但是链式队列增加了存储成本。
代码如下:
/**
* 基于链表的队列
*/
public class LinkQueue<T> {
/**
* 头指针:指向队首位置
*/
private Node head;
/**
* 尾指针:指向队尾位置
*/
private Node tail;
/**
* 入队操作
*
* @param data
* @return
*/
public boolean add(T data) {
Node node = new Node(data, null);
// 判断队列中是否有元素
if (tail == null) {
tail = node;
head = node;
} else {
tail.next = node;
tail = node;
}
return true;
}
/**
* 出队操作
*
* @return
*/
public T dequeue() {
if (head == null) {
throw new IndexOutOfBoundsException("Queue empty");
}
T data = (T) head.data;
head = head.next;
// 取出元素后,头指针为空,说明队列中没有元素,tail也需要制为空
if (head == null) {
tail = null;
}
return data;
}
/**
* 自定义内部类实现链表节点
*
* @param <T>
*/
class Node<T> {
private T data;
private Node next;
public Node(T data, Node node) {
this.data = data;
next = node;
}
}
}
优先队列
优先队列为一种不必遵循队列先进先出(FIFO)特性的特殊队列,优先队列跟普通队列一样都只有一个队头和一个队尾并且也是从队头出队,队尾入队,不过在优先队列中,每次入队时,都会按照入队数据项的关键值进行排序(从大到小、从小到大),这样保证了关键字最小的或者最大的项始终在队头,出队的时候优先级最高的就最先出队。
这个就像我们医院就医一样,急救的病人要比普通的病人先就诊。一起来看看优先队列的出队、入队操作:
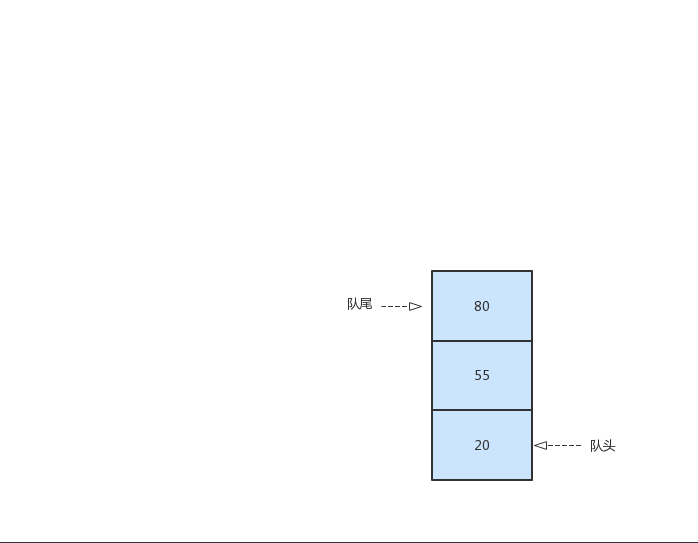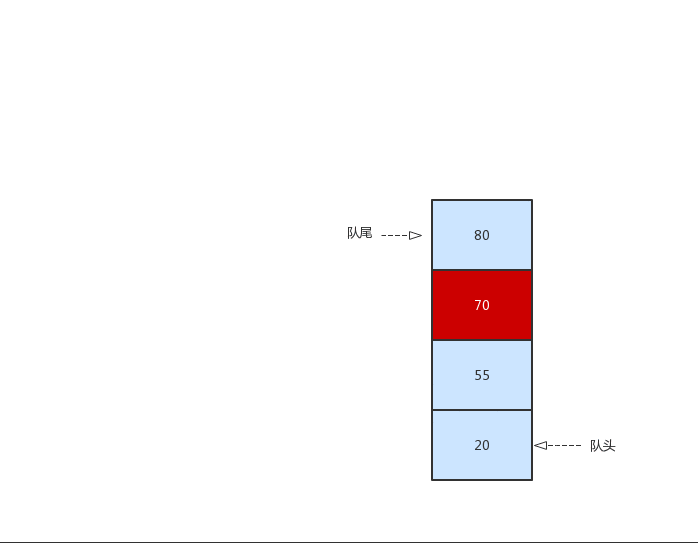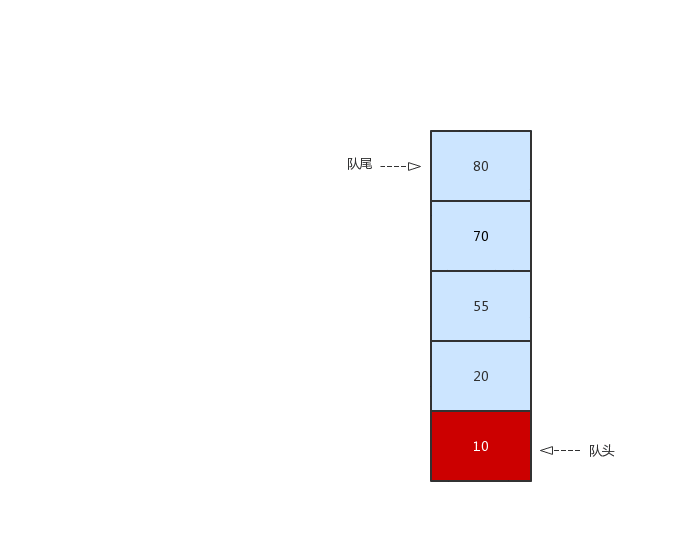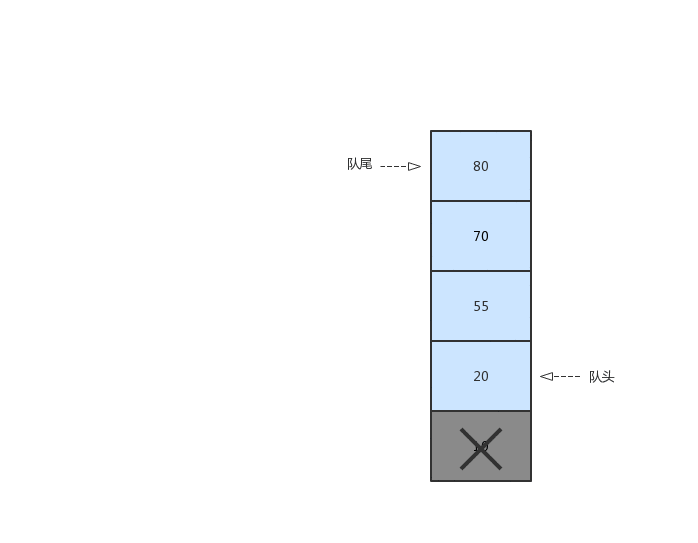
在上图中,我们规定数值越小优先级越高。我们每执行一次入队操作时,小的元素都会靠近头队,在出队的时候,元素小的也就先出队。
队列的应用
23. 合并K个升序链表
题目
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
解题分析
利用优先队列 PriorityQueue,如下图所示:
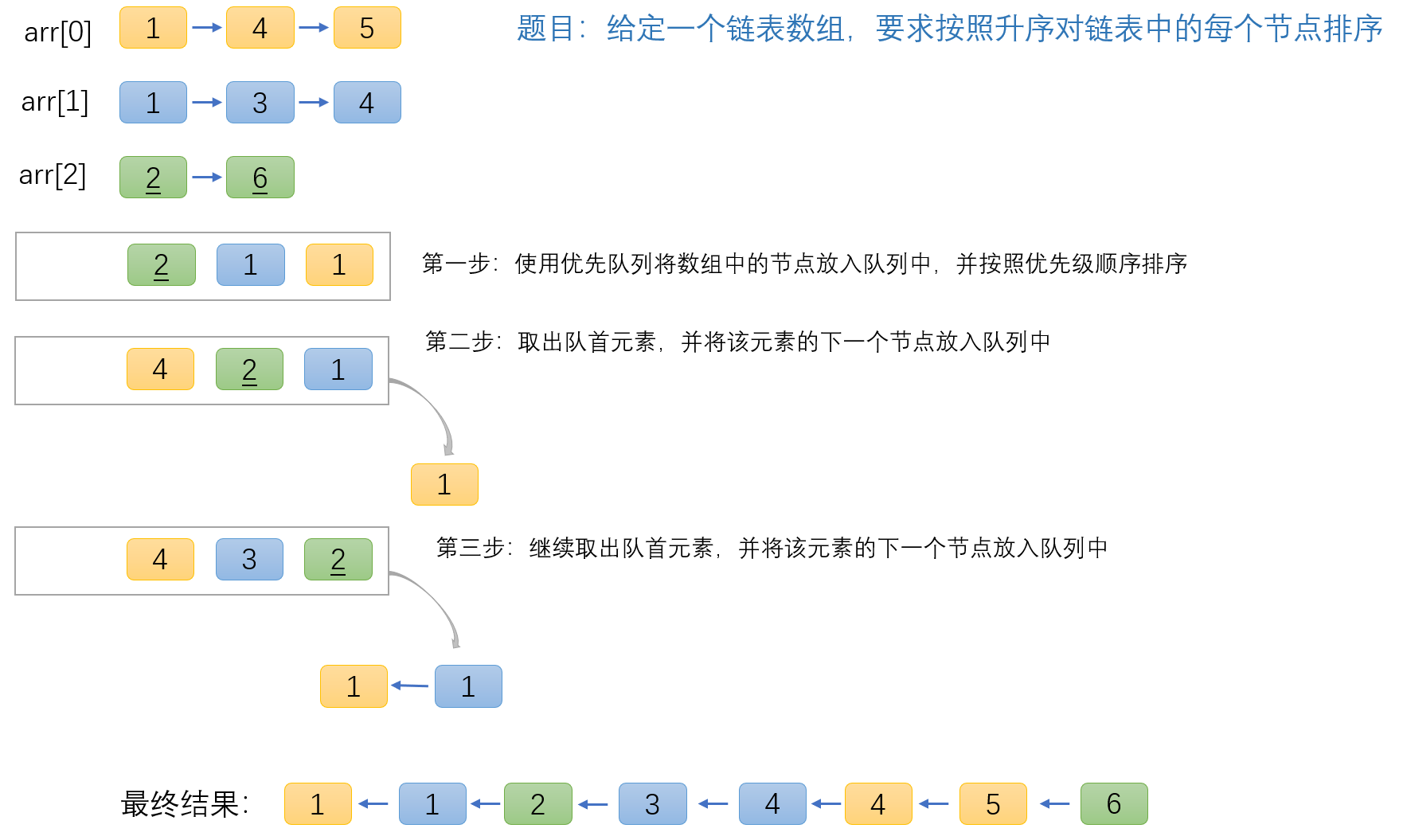
代码实现
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
//1、校验数组是否为空
if (lists == null || lists.length == 0) {
return null;
}
//2、使用优先队列对ListNode排序
PriorityQueue<ListNode> queue = new PriorityQueue<>(Comparator.comparing(node -> node.val));
for (ListNode node : lists) {
if (node != null) {
queue.add(node);
}
}
ListNode dummy = new ListNode(0);
ListNode tail = dummy;
while (!queue.isEmpty()) {
tail.next = queue.poll();
tail = tail.next;
if (tail.next != null) {
queue.add(tail.next);
}
}
return dummy.next;
}
}
总结
- 队列是一种遵循先进先出(FIFO)的数据结构
- 队列可以使用数组和链表实现,数组实现叫作顺序队列,链表实现叫作链式队列
- 循环队列解决了顺序队列的数据迁移带来的性能损耗的问题
- 双端队列是队头和队尾都可以进行入队、出队操作的队列
- 优先队列是一种不必遵循先进先出规则的队列,任意元素加入时,都会讲优先级最高的放入到队头



 浙公网安备 33010602011771号
浙公网安备 33010602011771号