数据结构与算法(五):栈
前面几篇文章主要是数据结构相关内容,我们介绍了数组、链表、树和二叉树等常用数据结构,本章我们再介绍一个常用数据结构 栈
什么是栈?
栈的定义
堆栈(stack)又称为栈或堆叠,是计算机科学里最重要且最基础的数据结构之一,它按照FILO(First In Last Out,后进先出)的原则存储数据。
关于“栈”,有一个非常贴切的例子,就是一摞叠在一起的盘子。我们平时放盘子的时候,都是从下往上一个一个放;取的时候,我们也是从上往下一个一个地依次取,不能从中间任意抽出。后进者先出,先进者后出,这就是典型的“栈”结构。
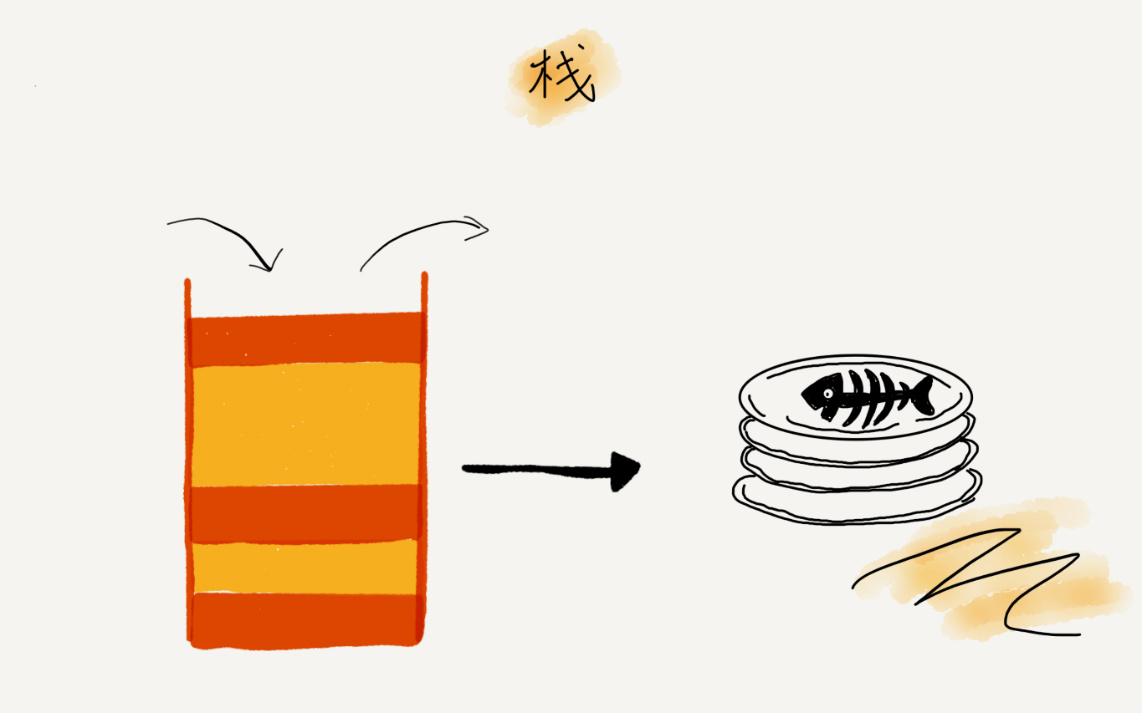
栈的相关概念
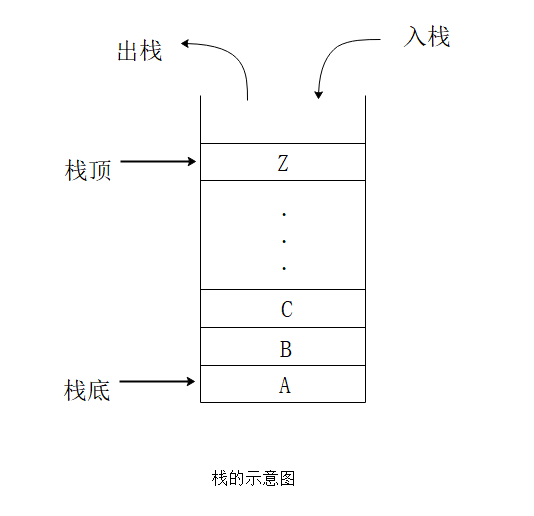
- 栈顶和栈底:允许元素插入与删除的一端称为
栈顶,另一端称为栈底 - 压栈:栈的插入操作,叫做进栈,也称压栈、入栈
- 弹栈:栈的删除操作,也叫做出栈
为什么需要栈?
-
栈是一种“操作受限”的线性表,只允许在一端插入和删除数据,其操作特性用数组和链表均可实现。
-
任何数据结构都是对特定应用场景的抽象,数组和链表虽然使用起来更加灵活,但却暴露了几乎所有的操作,难免会引发错误操作的风险。
-
当某个数据集合只涉及在某端插入和删除数据,且满足后进者先出,先进者后出的操作特性时,我们应该首选栈这种数据结构。
如何实现栈?
1、栈的API
从刚才栈的定义里,我们可以看出,栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。理解了栈的定义之后,我们看看栈主要有哪些API调用:
public class Stack<T> {
//压栈T
public void push(T t){}
//弹栈
public T pop(){}
//是否为空
public boolean isEmpty(){}
//栈中数据的数量
public int size(){}
//返回栈中最近添加的元素而不删除它
public T peek(){}
}
2、数组实现顺序栈
代码
public class Stack {
private int size = 0;
private int[] array;
public Stack() {
this(10);
}
public Stack(int init) {
if (init <= 0) {
init = 10;
}
array = new int[init];
}
/**
* 入栈
* @param item 入栈元素的值
*/
public void push(int item) {
if (size == array.length) {
array = Arrays.copyOf(array, size * 2);
}
array[size++] = item;
}
/**
* 获取栈顶元素,但是没有出栈
* @return
*/
public int peek() {
if (size == 0) {
throw new IndexOutOfBoundsException("栈里已经空啦");
}
return array[size - 1];
}
/**
* 出栈,同时获取栈顶元素
* @return
*/
public int pop() {
int item = peek();
size --; // 直接使元素个数减1,不需要真的清除元素,下次入栈会覆盖旧元素值
return item;
}
/**
* 栈是否满了
* @return
*/
public boolean isFull() {
return size == array.length;
}
/**
* 栈是否为空栈
* @return
*/
public boolean isEmpty() {
return size == 0;
}
public int size() {
return size;
}
}
了解了定义和基本操作,那它的操作的时间、空间复杂度是多少呢?
不管是顺序栈还是链式栈,我们存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中,只需要一两个临时变量存储空间,所以空间复杂度是 O(1)。
注意,这里存储数据需要一个大小为 n 的数组,并不是说空间复杂度就是 O(n)。因为,这 n 个空间是必须的,无法省掉。所以我们说空间复杂度的时候,是指除了原本的数据存储空间外,算法运行还需要额外的存储空间。
3、链表实现链式栈
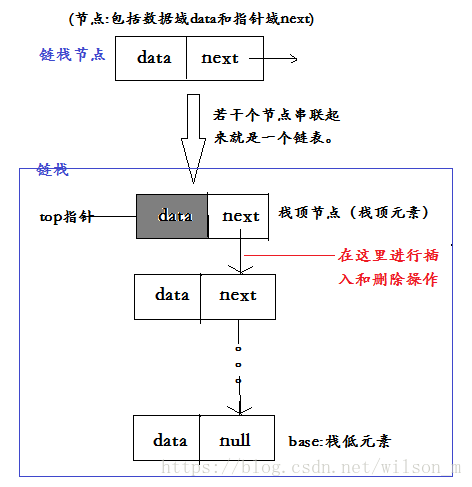
public class LinkStack {
/**
* 定义链栈的结点
* Object类型的数据域
* Node类型的指针域
*
*/
private class Node {
Object data;
Node next;
public Node() {
}
public Node(Object data, Node next) {
this.data = data;
this.next = next;
}
}
private Node top; //栈顶元素
private int size; //当前栈的大小
/**
* 创建空链栈
*/
public LinkStack() {
top = null;
}
/**
* 以data数据元素创建链式栈
*
* @param data
*/
public LinkStack(Object data) {
top = new Node(data, null);
size++;
}
/**
* 判断链栈是否为空栈
*
* @return
*/
public boolean isEmpty() {
return size == 0 ? true : false;
}
/**
* 返回链栈的长度
*
* @return
*/
public int length() {
return size;
}
/**
* 压栈(入栈)
*
* @param data
*/
public void push(Object data) {
// 让top指向新创建的元素,新元素的next引用指向原来的栈顶元素
top = new Node(data, top);
size++;
}
/**
* 出栈
*
* @return
*/
public Object pop() {
if (isEmpty()) {
System.out.println("目前是空栈,无法进行出栈!");
return "error!";
}
Node temp = top;
// 更新头结点
top = top.next;
// 释放原栈顶元素的next引用,删除指针指向
temp.next = null;
size--;
return temp.data;
}
/**
* 访问栈顶元素
*
* @return
*/
public Object peek() {
if (top != null) {
return top.data;
}
return "空栈,无栈顶元素!";
}
/**
* 遍历栈并打印栈内元素
*/
public void displayStack() {
while (top != null) {
System.out.println(top.data + "\t");
top = top.next;
}
}
/**
* 清空栈
*/
public void clear() {
top = null;
size = 0;
}
}
栈的应用
1、栈在函数调用中的应用
栈作为一个比较基础的数据结构,应用场景还是蛮多的。其中,比较经典的一个应用场景就是函数调用栈。
我们知道,操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。为了让你更好地理解,我们一块来看下这段代码的执行过程。
int main() {
int a = 1;
int ret = 0;
int res = 0;
ret = add(3, 5);
res = a + ret;
printf("%d", res);
reuturn 0;
}
int add(int x, int y) {
int sum = 0;
sum = x + y;
return sum;
}
从代码中我们可以看出,main() 函数调用了 add() 函数,获取计算结果,并且与临时变量 a 相加,最后打印 res 的值。为了让你清晰地看到这个过程对应的函数栈里出栈、入栈的操作,我画了一张图。图中显示的是,在执行到 add() 函数时,函数调用栈的情况。
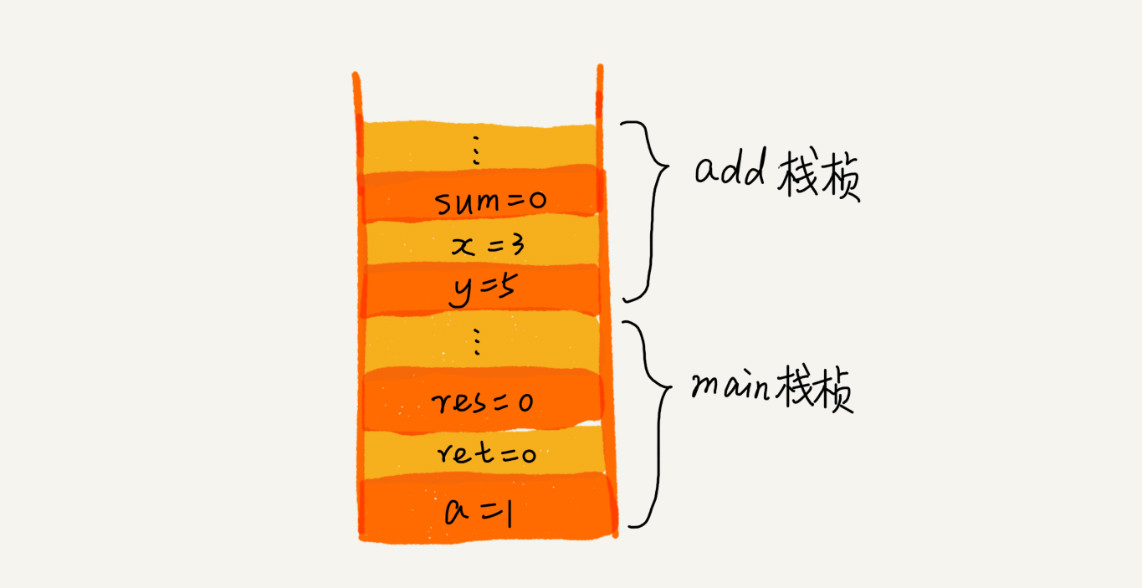
2、栈在表达式求值中的应用
再来看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。
为了方便解释,我将算术表达式简化为只包含加减乘除四则运算,比如:34+13*9+44-12/3。对于这个四则运算,我们人脑可以很快求解出答案,但是对于计算机来说,理解这个表达式本身就是个挺难的事儿。如果换作你,让你来实现这样一个表达式求值的功能,你会怎么做呢?
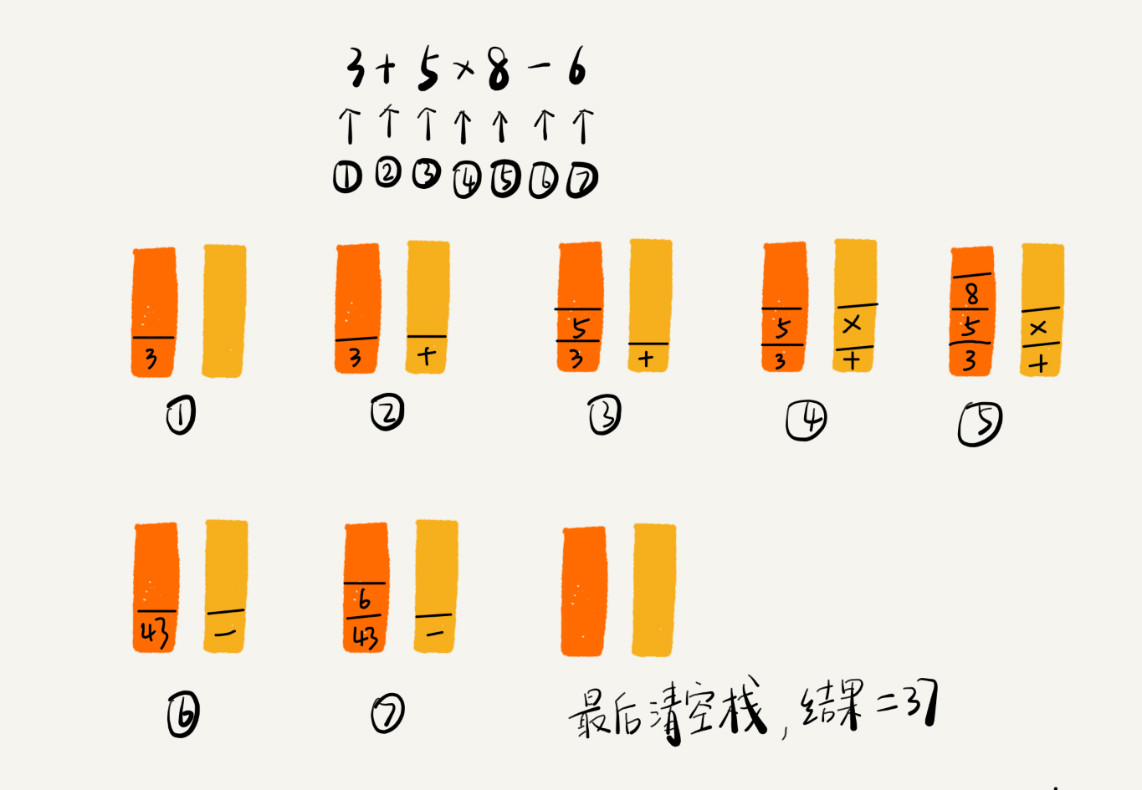
实际上,编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保存运算符的栈。我们从左向右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算符,就与运算符栈的栈顶元素进行比较。
如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。
将 3+5*8-6 这个表达式的计算过程画成了一张图,你可以结合图来理解计算过程。
代码
3、检测代码中括号匹配问题
题目
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
1、左括号必须用相同类型的右括号闭合。
2、左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
解题分析
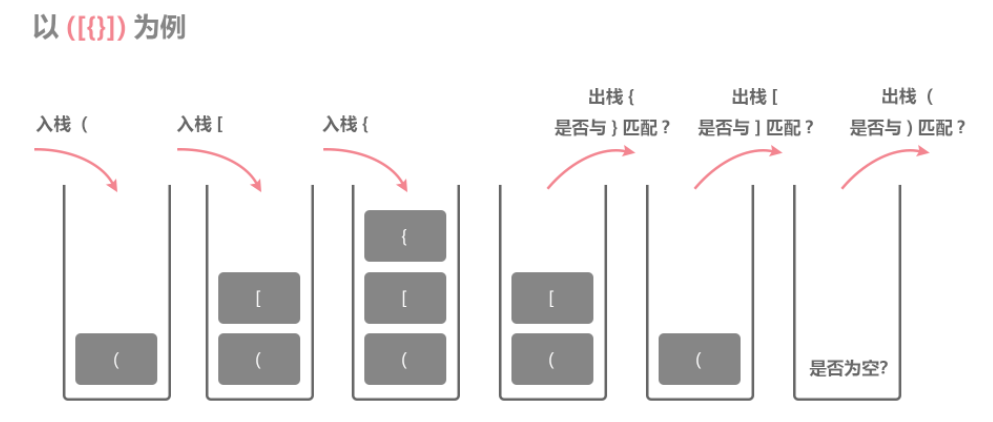
这是一个使用栈解决的经典的问题:思路就是创建一个栈,遇到左括号时就入栈,遇到右括号时就弹出栈顶元素,看当前的括号是否与弹出的匹配,只要有一次不匹配,就返回false,最后检查该栈是否为空即可。
代码
class Solution {
public boolean isValid(String s) {
HashMap<Character,Character> map = new HashMap<Character, Character>();
map.put('}','{');
map.put(']','[');
map.put(')','(');
Stack<Character> stack = new Stack<Character>();
for (char c : s.toCharArray()) {
if (map.containsKey(c)){
if (stack.isEmpty() || !stack.pop().equals(map.get(c))){
return false;
}
}else {
stack.push(c);
}
}
if (!stack.isEmpty()){
return false;
}
return true;
}
}
总结
- 栈是一种常用数据结构,遵循先进后出的原则
- 与数组相比,栈的操作是受限的,只能从头部入栈和出栈
- 栈可以由数组实现顺序栈,栈可以由链表实现链式栈
- 栈这种数据结构只需要知道其大概特性和常用API,至于对栈的深入理解和运用最好还是通过相关题目
- 记住百闻不如一见,百看不如一练


 浙公网安备 33010602011771号
浙公网安备 33010602011771号