【LeetCode】235. 二叉搜索树的最近公共祖先

算法现在就是大厂、外企的硬指标。开发、测开、测试，想往上总是绕不开的。

题目描述

难度：【简单】 标签：【二叉树】

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，
最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先
且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

题目地址：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

示例

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

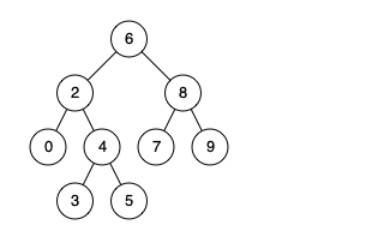
示例 1

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 
因为根据定义最近公共祖先节点可以为节点本身。

解题

参考官方题解。这题关键在于，给定的是一个二叉搜索树，要利用它的特性:

• 从根节点开始遍历
• 如果当前节点的值大于 p 和 q 的值，说明 p 和 q 应该在当前节点的左子树，因此将当前节点移动到它的左子节点
• 如果当前节点的值小于 p 和 q 的值，说明 p 和 q 应该在当前节点的右子树，因此将当前节点移动到它的右子节点。
• 如果都不满足，说明当前节点就是「分岔点」。此时，p 和 q 要么在当前节点的不同的子树中，要么其中一个就是当前节点。

这样就可以只使用一次遍历解决：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode cur = root;
        while (true) {
            if (cur.val > p.val && cur.val > q.val) {
                cur = cur.left;
            } else if (cur.val < p.val && cur.val < q.val) {
                cur = cur.right;
            } else {
                break;
            }
        }
        return cur;
    }
}