【LeetCode】111. 二叉树的最小深度（BFS 解题套路框架，要会默写）

一、BFS 知识点

BFS 就是广度优先 (Breadth first search)。与之对应的还有深度优先 (Depth first search)。

网上找到一篇文章，比较通俗易懂的介绍了这 2 者。

今天重点是 BFS ，用它解决比如找到从起点 start 到终点 target 的最近距离问题（黑色起点、红色终点）。

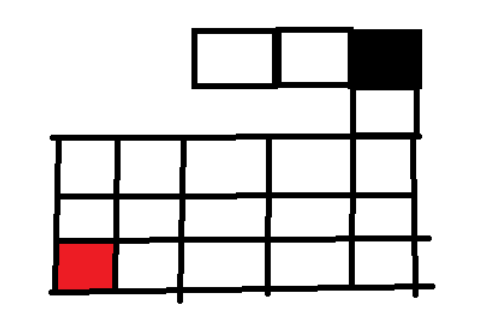
BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度可能比 DFS 大很多 。

BFS 的核心思想就是把一些问题抽象成图，从一个点开始，向四周开始扩散。

一般来说，我们写 BFS 算法都是用队列这种数据结构，每次将一个节点周围的所有节点加入队列。

这是框架，来自【labuladong】公众号的学习资源。这里要逐行阅读理解，并记忆。

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

代码里的一些方法说明：

• q.offer(start)，往队列尾部插入元素，当超出队列界限的时候，返回 false 。
• q.poll()，获取并删除Queue中的第一个元素。
• visited.add(start)，向 set 集合里添加元素。
• 队列 q 是 BFS 的核心数据结构。
• cur.adj()泛指 cur 相邻的节点，比如说二维数组中，cur 上下左右四面的位置就是相邻节点。
• visited 的主要作用是防止走回头路，大部分时候都是必须的。但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited。

二、BFS 解决二叉树的最小深度

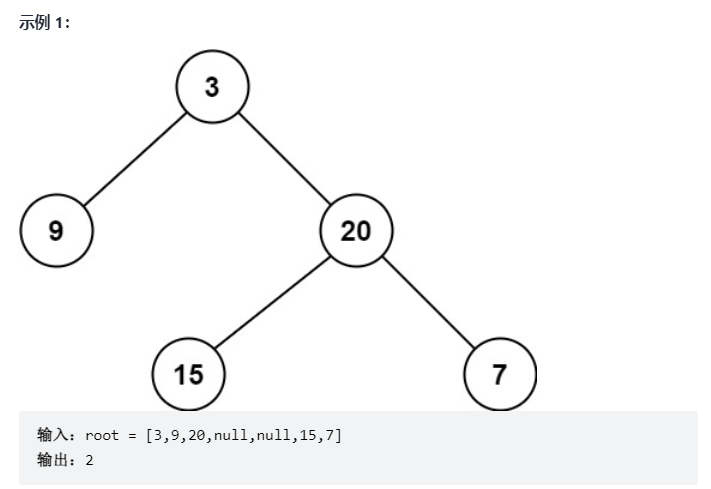
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

之前的做法：

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 左右孩子都为null，返回 1
        if (root.left == null && root.right == null) {
            return 1;
        }
        int leftHeight = minDepth(root.left);
        int rightHeight = minDepth(root.right);
        // 左右孩子有一个为null
        if (leftHeight == 0 || rightHeight == 0) {
            return leftHeight + rightHeight + 1;
        }
        // 左右孩子都不为null，返回比较最短的 + 1
        return Math.min(leftHeight, rightHeight) + 1;
    }
}

使用 BFS ，套用框架：

• 起点就是根节点
• 终点就是最靠近根节点的那个「叶子节点」
• 叶子节点就是两个子节点都是 null 的节点

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root); // 将起点加入队列
        int depth = 1; // root 本身就是一层，depth 初始化为 1

        while (!q.isEmpty()) {
            // 将当前队列中的所有节点向四周扩散
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                TreeNode cur = q.poll();  // 获取并删除Queue中的第一个元素
                /* 划重点：这里判断是否到达终点 */
                if (cur.left == null && cur.right == null) {
                    return depth;
                }
                /* 将 cur 的相邻节点加入队列 */
                if (cur.left != null) {
                    q.offer(cur.left);
                }
                if (cur.right != null) {
                    q.offer(cur.right);
                }
            }
            /* 这里增加步数 */
            depth++;
        }
        return depth;
    }
}