【小白学算法】7.树与二叉树

树是另一种存储结构。跟之前说的线性结构不同，树是一种一对多的数据结构。

一、树

这里的树跟现实中的大树很像，有根有叶。但是现实的大树根部有很多根须，而这里的树只有一个根结点。

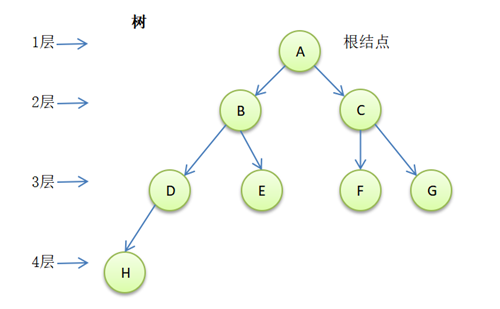
看图说话，了解下常用到的术语：

• 结点点：就是图里的一个个的圆圈了，也可以叫结点对象
• 根结点：顶部的结点A，数据结构的树只能有一个根结点
• 父结点：B是D、E的父结点，D是H的父结点
• 子结点：F是C的子结点
• 度：结点拥有的子树数量，B的度为2，D的度为1
• 叶结点：度为0的为叶结点，比如H、E、F、G
• 路径：从根结点到目标结点的路线，比如找D，就是A-B-D
• 高度&深度：树中结点的最大层数，上图为4
• 子树：B结点往下，C结点往下，这2部分就是A的子树
• 有序树：各子树从左至右有次序的，不能互换，则为有序树，否则为无序树
• 森林：是互不相交的树的集合，比如 B结点的子树 与 C结点的子树，就是森林

二、二叉树

有了树的概念，二叉树就好理解了。首先它得是树，上述的图其实就是个二叉树。
不过要注意的是，二叉树不一定非得有2个叉，每个结点最多有2个子结点的就是二叉树，其中又分左结点和右结点。

1.满二叉树：

该二叉树所有结点都存在左子树和右子树，并所有叶结点都在最后一层，看起来很完美。
这里结点的总数=2^n-1，n是层数。

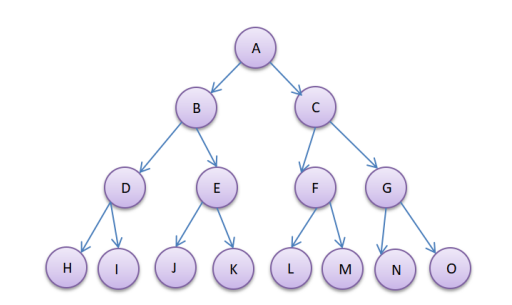
2.完全二叉树：

它的描述是这样的：对于一颗具有n个结点的二叉树按层序编号，
如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点
在二叉树中位置完全相同，那么这棵树就是完全二叉树。

说实话，这段描述咋一看有点绕，我初次看理解了好久（太笨了），现在我来描述下帮助理解。首先关注2个点：
1 满二叉树
2 按层序编号

这里直接参考上述的满二叉树的图。编号，就是我们给它的假想编号，就按照从上到下，从左到右来一次排序，图中是
A~O。

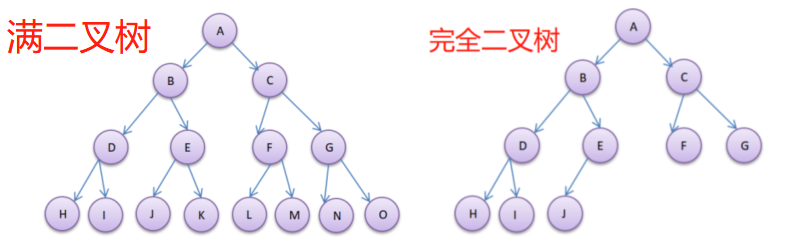
1. 完全二叉树
   结合示意图可以看出，右图存在的所有结点的编号，都与左边的满二叉树中的结点位置一一对应。所以，右图就是完全二叉树。
   

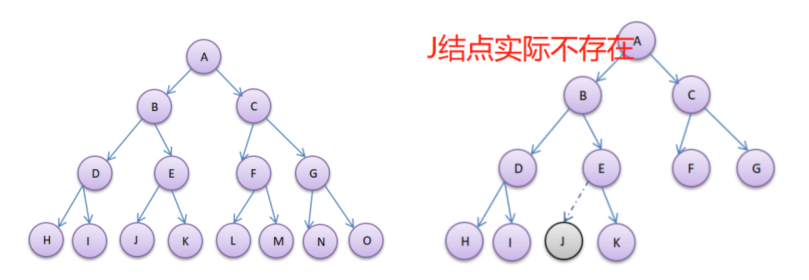
2. 非完全二叉树
   右图的二叉树中J结点实际是不存在的，未了示意用。你可以在心中给右侧图按照满二叉树进行编号，但是发现到J结点断掉了，
   因为此结点不存在，编号不连续了，所以就不是完全二叉树。
   

接下来，就准备二叉树的遍历了。