Matlab:回归分析(1)

1.多元线性回归

 1 %数据的输入
 2 x = [143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164];
 3 y = [88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102];
 4 %转换为列向量
 5 X = [ones(16,1) x'];
 6 Y = y';
 7 %回归分析及检验
 8 [b, bint, r, rint, states] = regress(Y, X, 0.05);
 9 b, bint, states
10 %作散点图和回归之后的图
11 z = b(1) + b(2)*x';
12 figure(1)
13 plot(x', Y, 'k+')
14 hold on
15 plot(x', z, 'r')
16 %作残差图
17 figure(2)
18 rcoplot(r, rint)

结果：

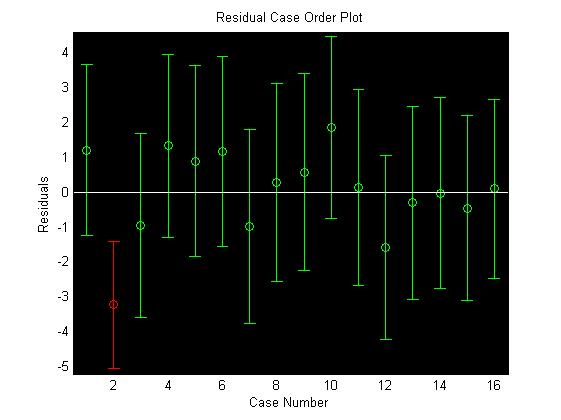
2.可线性化的一元非线性回归

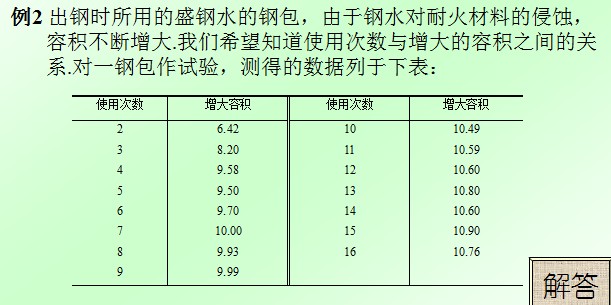
 根据数据散点图

配曲线，此题配的是倒指数曲线y = a*exp(b/x)其中a>0

1 function f = volum(beta, x)
2 f = beta(1) * exp(beta(2) ./ x);
 1 %输入数据
 2 x = 2:16;
 3 y = [6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
 4 %拟定回归系数的初值
 5 beta0 = [8 2]';
 6 %求回归系数
 7 [beta, r, J] = nlinfit(x', y', 'volum', beta0);
 8 beta
 9 %预测及作图
10 [Y, delta] = nlpredci('volum', x', beta, r, J);
11 %散点图
12 plot(x, y, 'k+')
13 hold on
14 %拟合图
15 plot(x, Y, 'r')

结果

3.多项式回归

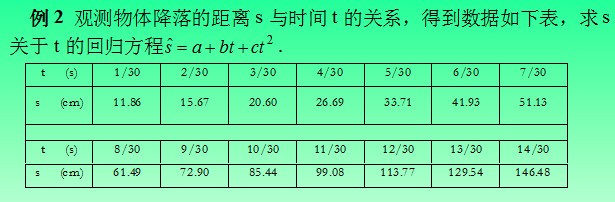
方法一：直接做二次多项式回归

1 t=1/30:1/30:14/30;
2 s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
3 %二次多项式回归
4 [p, S] = polyfit(t, s, 2);
5 p

结果：
p =489.2946   65.8896    9.1329

即为二次多项式系数 cba

方法二：化为多元线性回归

 1 t = 1/30:1/30:14/30;
 2 s = [11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
 3 %化为多元线性回归
 4 T = [ones(14, 1), t', (t.^2)'];
 5 [b, bint, r, rint, states] = regress(s', T, 0.05);
 6 b, states
 7 %预测及作图
 8 %参数p和S必须由多项式回归函数polyfit求出
 9 [p, S] = polyfit(t, s, 2);
10 Y = polyconf(p, t, S);%预测值
11 plot(t, s, 'k+', t, Y, 'r')

结果：
b =

    9.1329    65.8896   489.2946

states =

  1.0e+007 *

    0.0000    1.0378    0.0000    0.0000

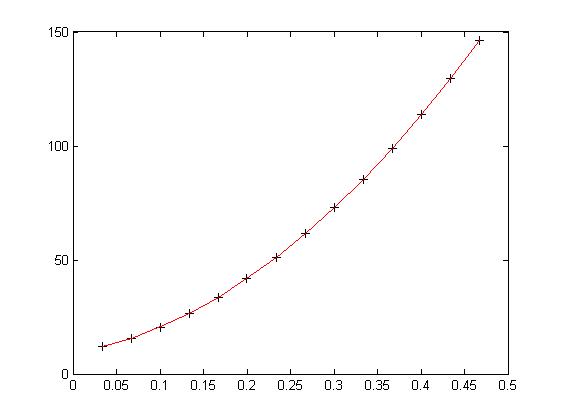
b即为二次多项式系数abc

 

posted @ 2013-08-14 22:47  瓶哥  Views(4327)  Comments(0)  Edit  收藏  举报