POJ_2488——骑士遍历棋盘,字典序走法

Description

Background
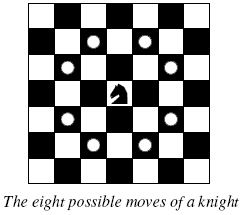
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?

Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

#include <cstdio>
#include <iostream>
#include <string>
#include <cstring>
//lexicographically first path
//题目output中出现了以上几个单词
//就是说骑士的移动步子是按照字典顺序来排列的
//首先对列进行排序较小的在前面，然后按行进行排序也是较小的在前面 
//我构造的xy坐标是按照SDL中的图形坐标，x往下递增，y往右递增
//转换成数学上的xy坐标就要先对列x做排序然后再对行y做排序 
int dirx[8]={-2,-2,-1,-1,1,1,2,2};
int diry[8]={-1,1,-2,2,-2,2,-1,1};

int T,p,q,mark[27][27];
std::string way;
bool DFS(int x,int y,int step)
{
   if(step==p*q)
      {
         return true;
      }
   for(int i=0;i<8;i++)
      {
         int dx=x+dirx[i];
         int dy=y+diry[i];
         if((dx>=1 && dx<=q) && (dy>=1 && dy<=p) && mark[dx][dy]!=1)
            {
               mark[dx][dy]=1;
               //当找到路径才会插入操作，所以在main函数循环中不需要清空string 
               if(DFS(dx,dy,step+1))
                  {
                     //在第0个位置插入1个字符
                     //先插入数字然后再插入字母，否则顺序颠倒 
                     way.insert(0,1,dy+'0');
                     way.insert(0,1,dx+'A'-1);
                     return true;   
                  }
               mark[dx][dy]=0;
            }
      }
   return false;
}
int main()
{
   scanf("%d",&T);
   for(int i=1;i<=T;i++)
      {
         scanf("%d%d",&p,&q);
         way.clear();//每次都要清空string
         bool find=false;
         for(int x=1;x<=q && !find;x++)
            {
               for(int y=1;y<=p;y++)
                  {
                     memset(mark,0,sizeof(mark));
                     mark[x][y]=1;
                     if(DFS(x,y,1))
                        {
                           //找到的话插入起始位置 
                           way.insert(0,1,y+'0');
                           way.insert(0,1,x+'A'-1);
                           find=true;
                           break;
                        }
                  }
            }
         std::cout<<"Scenario #"<<i<<":"<<std::endl;
         if(find)
            {
               //整体输出就行
               std::cout<<way<<std::endl<<std::endl;
            }
         else
            printf("impossible\n\n");
      }
   return 0;   
}