二叉树总结
此博客链接:https://www.cnblogs.com/ping2yingshi/p/13396766.html
概念
结点的度:结点拥有的子树的数目。
叶子:度为零的结点。
分支结点:度不为零的结点。
树的度:树中结点的最大的度。
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。
树的高度:树中结点的最大层次。
无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。
有序树:如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
定义
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。

二叉树性质
二叉树有以下几个性质:TODO(上标和下标)
性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
二叉树性质证明
2.1 性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)
证明:下面用"数学归纳法"进行证明。
(01) 当i=1时,第i层的节点数目为2{i-1}=2{0}=1。因为第1层上只有一个根结点,所以命题成立。
(02) 假设当i>1,第i层的节点数目为2{i-1}。这个是根据(01)推断出来的!
下面根据这个假设,推断出"第(i+1)层的节点数目为2{i}"即可。
由于二叉树的每个结点至多有两个孩子,故"第(i+1)层上的结点数目" 最多是 "第i层的结点数目的2倍"。即,第(i+1)层上的结点数目最大值=2×2{i-1}=2{i}。
故假设成立,原命题得证!
2.2 性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)
证明:在具有相同深度的二叉树中,当每一层都含有最大结点数时,其树中结点数最多。利用"性质1"可知,深度为k的二叉树的结点数至多为:
20+21+…+2k-1=2k-1
故原命题得证!
2.3 性质3:包含n个结点的二叉树的高度至少为log2 (n+1)
证明:根据"性质2"可知,高度为h的二叉树最多有2{h}–1个结点。反之,对于包含n个节点的二叉树的高度至少为log2(n+1)。
2.4 性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:因为二叉树中所有结点的度数均不大于2,所以结点总数(记为n)="0度结点数(n0)" + "1度结点数(n1)" + "2度结点数(n2)"。由此,得到等式一。
(等式一) n=n0+n1+n2
另一方面,0度结点没有孩子,1度结点有一个孩子,2度结点有两个孩子,故二叉树中孩子结点总数是:n1+2n2。此外,只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) n=n1+2n2+1
由(等式一)和(等式二)计算得到:n0=n2+1。原命题得证!
满二叉树,完全二叉树和二叉查找树
满二叉树
定义:高度为h,并且由2{h} –1个结点的二叉树,被称为满二叉树。
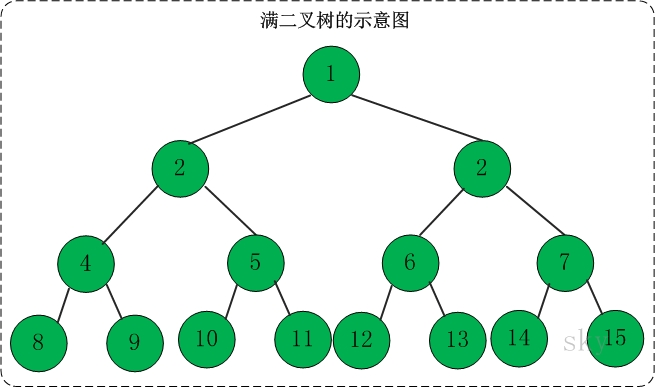
完全二叉树
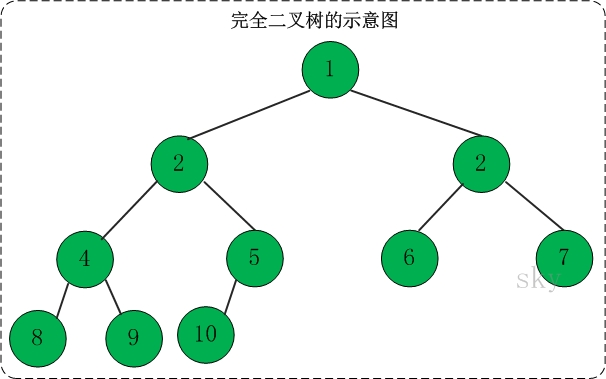
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
参考链接:https://www.cnblogs.com/skywang12345/p/3576328.html



