车的可用捕获量

此博客链接：https://www.cnblogs.com/ping2yingshi/p/12576257.html

车的可用捕获量（105min）

题目链接：https://leetcode-cn.com/problems/available-captures-for-rook/

在一个 8 x 8 的棋盘上，有一个白色车（rook）。也可能有空方块，白色的象（bishop）和黑色的卒（pawn）。它们分别以字符 “R”，“.”，“B” 和 “p” 给出。大写字符表示白棋，小写字符表示黑棋。

车按国际象棋中的规则移动：它选择四个基本方向中的一个（北，东，西和南），然后朝那个方向移动，直到它选择停止、到达棋盘的边缘或移动到同一方格来捕获该方格上颜色相反的卒。另外，车不能与其他友方（白色）象进入同一个方格。

返回车能够在一次移动中捕获到的卒的数量。
 

示例 1：

 

 

 

输入：[[".",".",".",".",".",".",".","."],

[".",".",".","p",".",".",".","."],

[".",".",".","R",".",".",".","p"],

[".",".",".",".",".",".",".","."],

[".",".",".",".",".",".",".","."],

[".",".",".","p",".",".",".","."],

[".",".",".",".",".",".",".","."],

[".",".",".",".",".",".",".","."]]
输出：3
解释：
在本例中，车能够捕获所有的卒。

示例 2：

 

 

 

输入：[[".",".",".",".",".",".",".","."]

,[".","p","p","p","p","p",".","."],

[".","p","p","B","p","p",".","."],

[".","p","B","R","B","p",".","."],

[".","p","p","B","p","p",".","."],

[".","p","p","p","p","p",".","."],

[".",".",".",".",".",".",".","."],

[".",".",".",".",".",".",".","."]]
输出：0
解释：
象阻止了车捕获任何卒。

示例 3：

 

 

 

输入：[[".",".",".",".",".",".",".","."],

[".",".",".","p",".",".",".","."],

[".",".",".","p",".",".",".","."],

["p","p",".","R",".","p","B","."],

[".",".",".",".",".",".",".","."],

[".",".",".","B",".",".",".","."],

[".",".",".","p",".",".",".","."],

[".",".",".",".",".",".",".","."]]
输出：3
解释：
车可以捕获位置 b5，d6 和 f5 的卒。

题解：

         题意：

                    前言：哈哈哈，此题简直了，对于本来就不会玩国际象棋的我来说，题目读的一愣一愣的，请教我弟弟，国际象棋怎么下的，还在电脑上玩了一把国际象棋，正常死了，后来还是看别人的题解加上我弟的解                       说，终 于明白题目意思了。

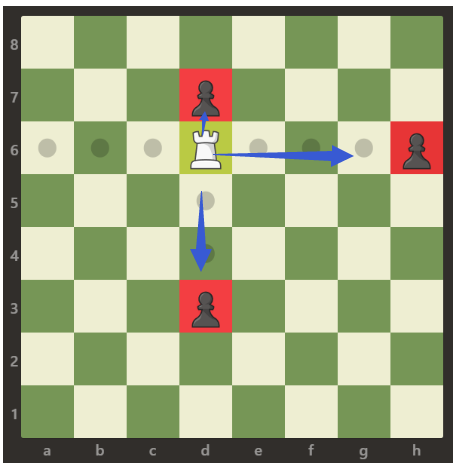
                    题目意思是说给你一个车（代码中用字母R表示，图形中带着像小皇冠的是车），这个车可以在上下左右四个方向移动，注意这里车是可以直线移动（走几个格子都可以，只要在和车同一直                     线上的卒车都可以吃掉）。但是呢，如果车旁边有象（代码用字母B表示，图形中用表示象）时，车不能和象在同一个方格中，也不能越过象去吃卒。

                   题目要求： 返回车能够在一次移动中捕获到的卒的数量，这里要理解为车一次移动可以捕获多少卒，但是我可以选择不同方向移动一次。

                  例如：

                   题目中给的示例1，车可以向上下右三个方向移动一次都可以捕获卒。我感觉这里题目应该说，返回车能够在一次移动中捕获到卒的所有可能数量。这样可更好理解题意。

                  

 

             思路：

                       1.找到车的位置。

                       2.判断车的上下左右四个方向上没有象存在的卒有多少。

  代码如下：

class Solution {
    public int numRookCaptures(char[][] board) {
        int count=0;
        for(int i=0;i<8;i++) //行
            for(int j=0;j<8;j++)//列
                {
                    if(board[i][j]=='R')//先找到车
                        {//然后判断四个方向有没有卒
                            for(int h=i;h>=0&&board[h][j]!='B';h--)//上
                                if(board[h][j]=='p')
                                {
                                    count++;
                                    break;
                                }
                            for(int h=i;h<8&&board[h][j]!='B';h++)//下
                                if(board[h][j]=='p')
                                 {
                                    count++;
                                    break;
                                 }
                            for(int h=j;h>=0&&board[i][h]!='B';h--)//左
                                if(board[i][h]=='p')
                                    {
                                    count++;
                                    break;
                                    }
                            for(int h=j;h<8&&board[i][h]!='B';h++)//右
                                if(board[i][h]=='p')
                                   {
                                    count++;
                                    break;
                                   }
                        }
                }

        return count;
    }
}