折线分割平面

此博客链接：https://www.cnblogs.com/ping2yingshi/p/12485742.html

1.折线分割平面（20min）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2050

Problem Description

我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

 

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

 

Sample Input

2

1

2

 

Sample Output

2

7

题解：

        题意：用折线最多能把平面分成几个区域。

        方法：递推。

        思路：

                 1.猜测推导过程：

                    已知当n=1时，平面能被分成2个区域；

                            当=2时，平面能被分成7个区域；

                     画出当n=3时，平面能被分成16个区域。

                 由以上推导可知，当n=2时和n=1时中间差了5，当n=3时和n=2时中间差了9，

                 由此可知，当n=i时，和n=i-1时中间差了4*i-3，所以推导公式为D(n)=D(n-1)+4*n-3。

                    

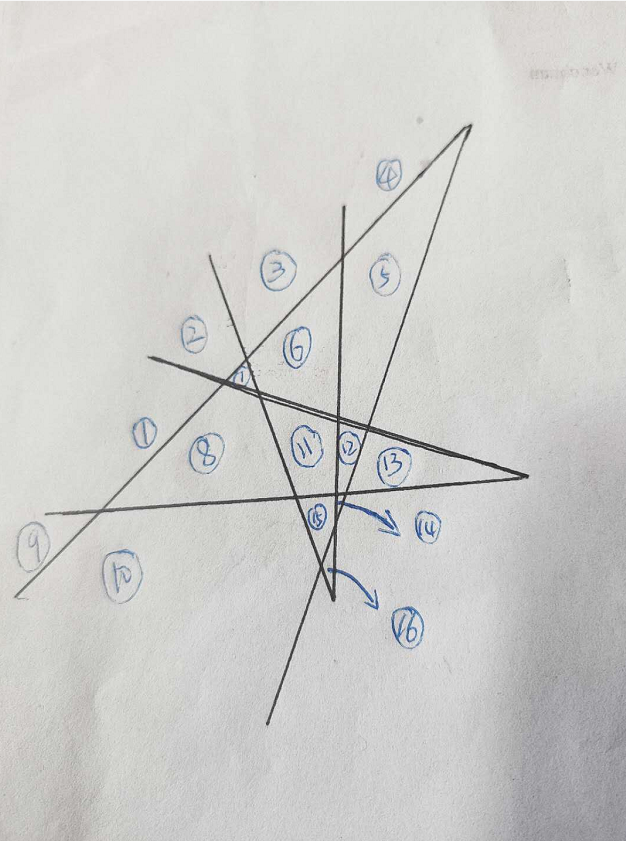
               注意：在画n=3时，在n=2的基础上画，画其中一条折线时，需要注意是穿过4条射线。

               以上题目是我自己猜测的，因为这种题目最后肯定是一个公式能解决的，所以我使用猜测法，正好猜对了。

              2.真正推导过程：

             

 

 

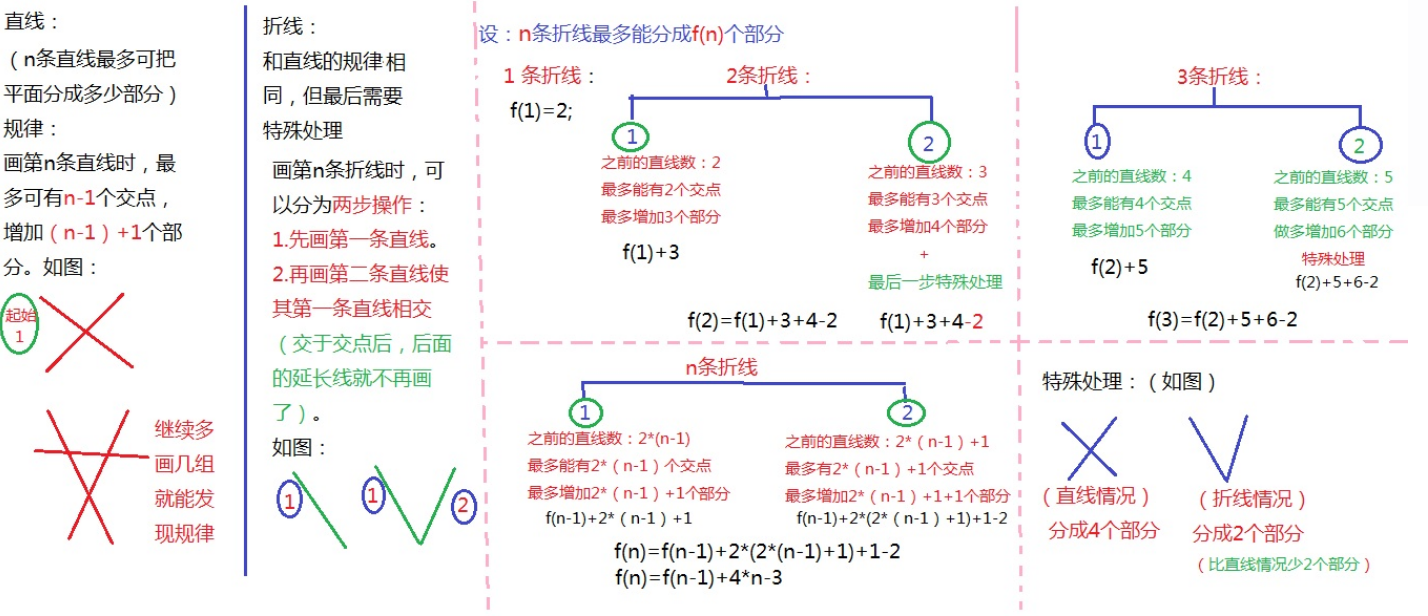
                          这是一个人写了博客，我感觉画的图还是挺容易理解的，但是文字表述的不是特别清楚博客链接：https://blog.csdn.net/hpulw/article/details/50579567

                           这道题主要是从直线过度到折线思想。主要思路如下：

                          1.直线思想：

                

                           

 

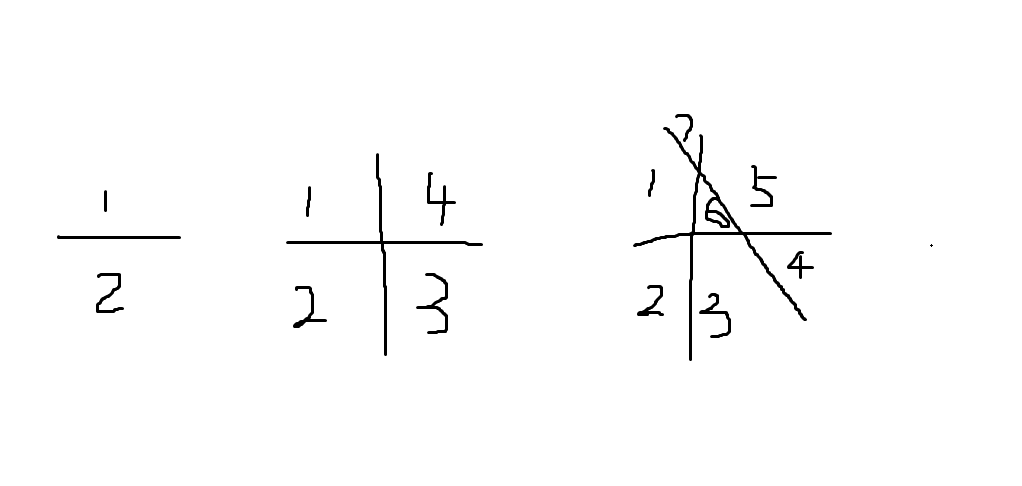
                            由图可以看出，每增加一条直线，增加的区域数正好等于当前直线个数，所以直线最多区域个数为：D(n)=D（n-1）+n。

                            2.折线思想：

                       

 

 

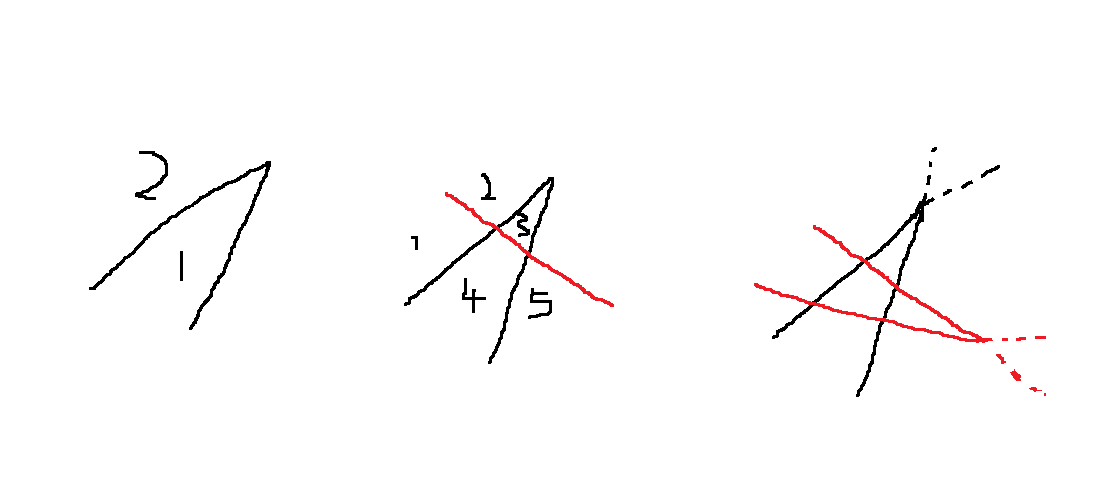
                            可以把直线当成直线处理，由上图可知：

                             1.当n=2时：

                               当增加第二条折线的第一条直线时，现在有三条直线，增加了三个区域；

                               当增加第二条折线的第二条直线时，现在有四条直线，增加了4个区域，但是由于不是直线，两条直线相交处的区域不存在，要减去两个区域，所以D(3)=D(2)+3+4-2；

                             3.当有n=i条折线时：

                               参看上图n条折线写法。

                               

 代码如下：

import java.util.Scanner;


public class test {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
       Scanner scan=new Scanner(System.in);
            int C=scan.nextInt();
              while(C>0)
              {
                  int n=scan.nextInt();
                  long sum=2;
           
                  for(int i=2;i<=n;i++)
                  {
                    sum=sum+4*i-3;
                  }      
                 
               System.out.println(sum);
               
              C--; 
       }

    }

}

 2.多数元素（35min）

题目链接：https://leetcode-cn.com/problems/majority-element/

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [3,2,3]
输出: 3
示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

题解：

         方法：题目给定多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素那么对数组排序后，中间数一定是次数出现最多的数。

         思路：先对数组进行排序，然后取数组中间元素。

代码如下：

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length/2];
    }
}