CGAL入门——凸壳算法

一、凸壳算法

　　凸壳是能包含点集合的最小凸多边形，即凸壳是点集合的一个子集，将这个子集的点连接起来可以包含点集中所有的点。

 

二、数组中点的凸壳

#include <iostream>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/convex_hull_2.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K; //predicates精确，constructions不精确的内核

typedef K::Point_2 Point_2;

//计算数组中点的 2D 凸壳，
int array_convex_hull_2()
{
    Point_2 points[5] = { Point_2(0,0), Point_2(10,0), Point_2(10,10), Point_2(6,5), Point_2(4,1) };
    Point_2 result[5];
    //输入的开始指针points,结束指针points+5,结果数组的开始指针result
    Point_2 *ptr = CGAL::convex_hull_2(points, points + 5, result);
    std::cout << ptr - result << " points on the convex hull:" << std::endl;//指针差值为凸壳上有多少个点
    for (int i = 0; i < ptr - result; i++) 
    {
        std::cout << result[i] << std::endl;//输出凸壳上的点
    }
    
    return 0;
}

输出结果

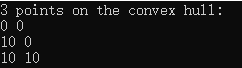
 这里使用的是精确谓词不精确构造的核(Exact_predicates_inexact_constructions_kernel)，因为凸壳算法只对输入点的坐标和方向做比较。

convex_hull_2函数有三个输入参数：输入的开始指针,结束指针,结果数组的开始指针；一个输出参数：指针(ptr)，这个指针是个边界指针，指向最后一个凸壳点的后面，所以指针差(ptr-result)是凸壳上点的数量。

 

三、vector中点的凸壳

#include <iostream>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K; //predicates精确，constructions不精确的内核

typedef K::Point_2 Point_2;
typedef std::vector<Point_2> Points;

//计算vector中点的 2D 凸壳
int vector_convex_hull_2()
{
    Points points, result;
    points.push_back(Point_2(0, 0));
    points.push_back(Point_2(10, 0));
    points.push_back(Point_2(10, 10));
    points.push_back(Point_2(6, 5));
    points.push_back(Point_2(4, 1));
    //输入的开始指针,结束指针,结果的开始指针
    CGAL::convex_hull_2(points.begin(), points.end(), std::back_inserter(result));//输出迭代器back_inserter在递增时不执行任何操作，而是调用result.push_back(..)赋值
    std::cout << result.size() << " points on the convex hull" << std::endl;
    for (int i = 0; i < result.size(); i++)
    {
        std::cout << result[i] << std::endl;
    }
    return 0;
}

输出结果

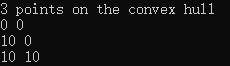
 同样的convex_hull_2也是三个输入参数，但是这里不需要返回边界指针了，也不需要预设结果的大小，但它需要动态增长，所以这里不能简单输入result.begin()，要用帮助器函数生成的输出迭代器back_inserter，这个迭代器可以在插入值调用push_back