LSTM模型与前向反向传播算法
在循环神经网络(RNN)模型与前向反向传播算法中,我们总结了对RNN模型做了总结。由于RNN也有梯度消失的问题,因此很难处理长序列的数据,大牛们对RNN做了改进,得到了RNN的特例LSTM(Long Short-Term Memory),它可以避免常规RNN的梯度消失,因此在工业界得到了广泛的应用。下面我们就对LSTM模型做一个总结。
1. 从RNN到LSTM
在RNN模型里,我们讲到了RNN具有如下的结构,每个序列索引位置t都有一个隐藏状态$h^{(t)}$。
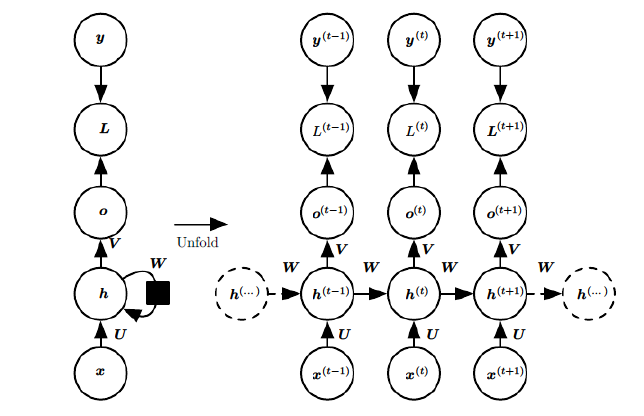
如果我们略去每层都有的$o^{(t)}, L^{(t)}, y^{(t)}$,则RNN的模型可以简化成如下图的形式:
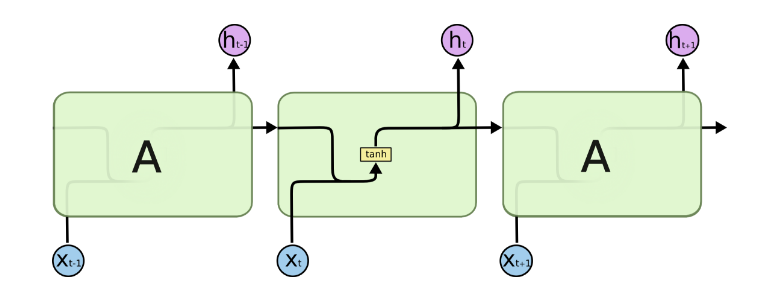
图中可以很清晰看出在隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$得到。得到$h^{(t)}$后一方面用于当前层的模型损失计算,另一方面用于计算下一层的$h^{(t+1)}$。
由于RNN梯度消失的问题,大牛们对于序列索引位置t的隐藏结构做了改进,可以说通过一些技巧让隐藏结构复杂了起来,来避免梯度消失的问题,这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种,这里我们以最常见的LSTM为例讲述。LSTM的结构如下图:
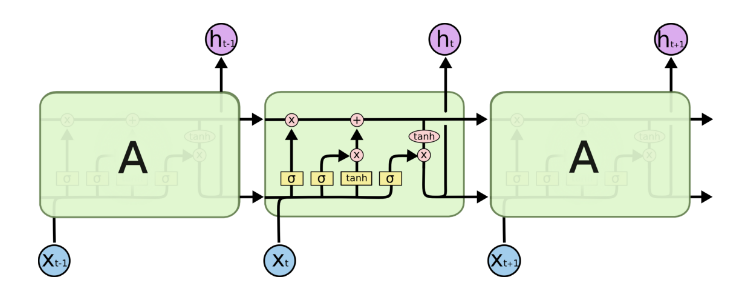
可以看到LSTM的结构要比RNN的复杂的多,真佩服牛人们怎么想出来这样的结构,然后这样居然就可以解决RNN梯度消失的问题?由于LSTM怎么可以解决梯度消失是一个比较难讲的问题,我也不是很熟悉,这里就不多说,重点回到LSTM的模型本身。
2. LSTM模型结构剖析
上面我们给出了LSTM的模型结构,下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。
从上图中可以看出,在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态$h^{(t)}$,还多了另一个隐藏状态,如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State),记为$C^{(t)}$。如下图所示:
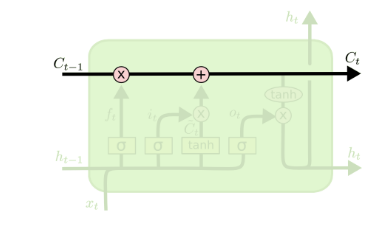
除了细胞状态,LSTM图中还有了很多奇怪的结构,这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门,输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门,输入门和输出门以及细胞状态。
2.1 LSTM之遗忘门
遗忘门(forget gate)顾名思义,是控制是否遗忘的,在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示:
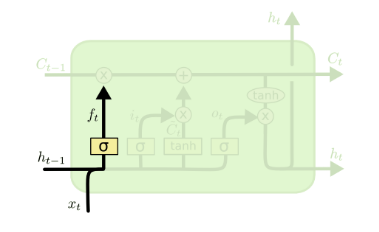
图中输入的有上一序列的隐藏状态$h^{(t-1)}$和本序列数据$x^{(t)}$,通过一个激活函数,一般是sigmoid,得到遗忘门的输出$f^{(t)}$。由于sigmoid的输出$f^{(t)}$在[0,1]之间,因此这里的输出f^{(t)}代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为:$$f^{(t)} = \sigma(W_fh^{(t-1)} + U_fx^{(t)} + b_f)$$
其中$W_f, U_f, b_f$为线性关系的系数和偏倚,和RNN中的类似。$\sigma$为sigmoid激活函数。
2.2 LSTM之输入门
输入门(input gate)负责处理当前序列位置的输入,它的子结构如下图:

从图中可以看到输入门由两部分组成,第一部分使用了sigmoid激活函数,输出为$i^{(t)}$,第二部分使用了tanh激活函数,输出为$a^{(t)}$, 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为:$$i^{(t)} = \sigma(W_ih^{(t-1)} + U_ix^{(t)} + b_i)$$$$a^{(t)} =tanh(W_ah^{(t-1)} + U_ax^{(t)} + b_a)$$
其中$W_i, U_i, b_i, W_a, U_a, b_a,$为线性关系的系数和偏倚,和RNN中的类似。$\sigma$为sigmoid激活函数。
2.3 LSTM之细胞状态更新
在研究LSTM输出门之前,我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态$C^{(t)}$。我们来看看从细胞状态$C^{(t-1)}$如何得到$C^{(t)}$。如下图所示:
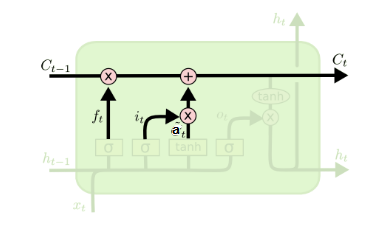
细胞状态$C^{(t)}$由两部分组成,第一部分是$C^{(t-1)}$和遗忘门输出$f^{(t)}$的乘积,第二部分是输入门的$i^{(t)}$和$a^{(t)}$的乘积,即:$$C^{(t)} = C^{(t-1)} \odot f^{(t)} + i^{(t)} \odot a^{(t)}$$
其中,$\odot$为Hadamard积,在DNN中也用到过。
2.4 LSTM之输出门
有了新的隐藏细胞状态$C^{(t)}$,我们就可以来看输出门了,子结构如下:
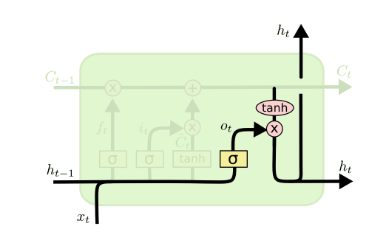
从图中可以看出,隐藏状态$h^{(t)}$的更新由两部分组成,第一部分是$o^{(t)}$, 它由上一序列的隐藏状态$h^{(t-1)}$和本序列数据$x^{(t)}$,以及激活函数sigmoid得到,第二部分由隐藏状态$C^{(t)}$和tanh激活函数组成, 即:$$o^{(t)} = \sigma(W_oh^{(t-1)} + U_ox^{(t)} + b_o)$$$$h^{(t)} = o^{(t)} \odot tanh(C^{(t)})$$
通过本节的剖析,相信大家对于LSTM的模型结构已经有了解了。当然,有些LSTM的结构和上面的LSTM图稍有不同,但是原理是完全一样的。
3. LSTM前向传播算法
现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态$h^{(t)}, C^{(t)}$,模型参数几乎是RNN的4倍,因为现在多了$W_f, U_f, b_f, W_a, U_a, b_a, W_i, U_i, b_i, W_o, U_o, b_o$这些参数。
前向传播过程在每个序列索引位置的过程为:
1)更新遗忘门输出:$$f^{(t)} = \sigma(W_fh^{(t-1)} + U_fx^{(t)} + b_f)$$
2)更新输入门两部分输出:$$i^{(t)} = \sigma(W_ih^{(t-1)} + U_ix^{(t)} + b_i)$$$$a^{(t)} = tanh(W_ah^{(t-1)} + U_ax^{(t)} + b_a)$$
3)更新细胞状态:$$C^{(t)} = C^{(t-1)} \odot f^{(t)} + i^{(t)} \odot a^{(t)}$$
4)更新输出门输出:$$o^{(t)} = \sigma(W_oh^{(t-1)} + U_ox^{(t)} + b_o)$$$$h^{(t)} = o^{(t)} \odot tanh(C^{(t)})$$
5)更新当前序列索引预测输出:$$\hat{y}^{(t)} = \sigma(Vh^{(t)} + c)$$
4. LSTM反向传播算法推导关键点
有了LSTM前向传播算法,推导反向传播算法就很容易了, 思路和RNN的反向传播算法思路一致,也是通过梯度下降法迭代更新我们所有的参数,关键点在于计算所有参数基于损失函数的偏导数。
在RNN中,为了反向传播误差,我们通过隐藏状态$h^{(t)}$的梯度$\delta^{(t)}$一步步向前传播。在LSTM这里也类似。只不过我们这里有两个隐藏状态$h^{(t)}$和$C^{(t)}$。这里我们定义两个$\delta$,即:$$\delta_h^{(t)} = \frac{\partial L}{\partial h^{(t)}}$$$$\delta_C^{(t)} = \frac{\partial L}{\partial C^{(t)}}$$
为了便于推导,我们将损失函数$L(t)$分成两块,一块是时刻$t$位置的损失$l(t)$,另一块是时刻$t$之后损失$L(t+1)$,即:$$L(t) = \begin{cases} l(t) + L(t+1) & \text{if} \, t < \tau \\ l(t) & \text{if} \, t = \tau\end{cases}$$
而在最后的序列索引位置$\tau$的$\delta_h^{(\tau)}$和 $\delta_C^{(\tau)} $为:$$\delta_h^{(\tau)} =(\frac{\partial o^{(\tau)}}{\partial h^{(\tau)}})^T\frac{\partial L^{(\tau)}}{\partial o^{(\tau)}} = V^T(\hat{y}^{(\tau)} - y^{(\tau)})$$$$\delta_C^{(\tau)} =(\frac{\partial h^{(\tau)}}{\partial C^{(\tau)}})^T\frac{\partial L^{(\tau)}}{\partial h^{(\tau)}} = \delta_h^{(\tau)} \odot o^{(\tau)} \odot (1 - tanh^2(C^{(\tau)}))$$
接着我们由$\delta_C^{(t+1)},\delta_h^{(t+1)}$反向推导$\delta_h^{(t)}, \delta_C^{(t)}$。
$\delta_h^{(t)}$的梯度由本层t时刻的输出梯度误差和大于t时刻的误差两部分决定,即:$$ \delta_h^{(t)} =\frac{\partial L}{\partial h^{(t)}} =\frac{\partial l(t)}{\partial h^{(t)}} + ( \frac{\partial h^{(t+1)}}{\partial h^{(t)}})^T\frac{\partial L(t+1)}{\partial h^{(t+1)}} = V^T(\hat{y}^{(t)} - y^{(t)}) + (\frac{\partial h^{(t+1)}}{\partial h^{(t)}})^T\delta_h^{(t+1)} $$
整个LSTM反向传播的难点就在于$ \frac{\partial h^{(t+1)}}{\partial h^{(t)}}$这部分的计算。仔细观察,由于$h^{(t)} = o^{(t)} \odot tanh(C^{(t)})$, 在第一项$o^{(t)}$中,包含一个$h$的递推关系,第二项$tanh(C^{(t)})$就复杂了,$tanh$函数里面又可以表示成:$$C^{(t)} = C^{(t-1)} \odot f^{(t)} + i^{(t)} \odot a^{(t)}$$
$tanh$函数的第一项中,$f^{(t)} $包含一个$h$的递推关系,在$tanh$函数的第二项中,$i^{(t)}$和$a^{(t)}$都包含$h$的递推关系,因此,最终$ \frac{\partial h^{(t+1)}}{\partial h^{(t)}}$这部分的计算结果由四部分组成。即:
$$\Delta C = o^{(t+1)} \odot [1-tanh^2(C^{(t+1)})]$$
$$\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = diag[o^{(t+1)} \odot (1-o^{(t+1)}) \odot tanh(C^{(t+1)})]W_o + diag[\Delta C \odot f^{(t+1)} \odot (1-f^{(t+1)}) \odot C^{(t)}] W_f+ diag \{ \Delta C \odot i^{(t+1)} \odot [1-(a^{(t+1)})^2] \} W_a + diag [\Delta C \odot a^{(t+1)} \odot i^{(t+1)} \odot (1-i^{(t+1)})]W_i$$
而$\delta_C^{(t)}$的反向梯度误差由前一层$\delta_C^{(t+1)}$的梯度误差和本层的从$h^{(t)}$传回来的梯度误差两部分组成,即:$$\delta_C^{(t)} =(\frac{\partial C^{(t+1)}}{\partial C^{(t)}} )^T\frac{\partial L}{\partial C^{(t+1)}} + (\frac{\partial h^{(t)}}{\partial C^{(t)}} )^T\frac{\partial L}{\partial h^{(t)}}= (\frac{\partial C^{(t+1)}}{\partial C^{(t)}} )^T\delta_C^{(t+1)} + \delta_h^{(t)} \odot o^{(t)} \odot (1 - tanh^2(C^{(t)})) = \delta_C^{(t+1)} \odot f^{(t+1)} + \delta_h^{(t)} \odot o^{(t)} \odot (1 - tanh^2(C^{(t)}))$$
有了$\delta_h^{(t)}$和$\delta_C^{(t)}$, 计算这一大堆参数的梯度就很容易了,这里只给出$W_f$的梯度计算过程,其他的$U_f, b_f, W_a, U_a, b_a, W_i, U_i, b_i, W_o, U_o, b_o,V, c$的梯度大家只要照搬就可以了。$$\frac{\partial L}{\partial W_f} =\sum\limits_{t=1}^{\tau} [\delta_C^{(t)} \odot C^{(t-1)} \odot f^{(t)}\odot(1-f^{(t)})] (h^{(t-1)})^T$$
5. LSTM小结
LSTM虽然结构复杂,但是只要理顺了里面的各个部分和之间的关系,进而理解前向反向传播算法是不难的。当然实际应用中LSTM的难点不在前向反向传播算法,这些有算法库帮你搞定,模型结构和一大堆参数的调参才是让人头痛的问题。不过,理解LSTM模型结构仍然是高效使用的前提。
(欢迎转载,转载请注明出处。欢迎沟通交流: liujianping-ok@163.com)
参考资料:
1) Neural Networks and Deep Learning by By Michael Nielsen
2) Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville


 浙公网安备 33010602011771号
浙公网安备 33010602011771号