C++函数

c++中的函数问题

一、为什么使用函数

函数的作用：c++继承了c语言的全部语法，在面向过程的结构化程序设计中，函数是模块划分的基本单位，撒对处理问题过程的一种抽象。而在面向对象的程序设计中，函数同样有着重要作用，它是面向对象程序设计中对功能的抽象。一个较为复杂的系统往往需要划分为若干个子系统，然后对这些子系统分别进行开发和调试，而在c++中就把这种子程序体现为函数。
使用函数的好处：函数编写好后，可以被重复使用，使用时可以只关心函数的功能和使用方法而不必关心函数功能的具体实现，这样有利于代码重用，可以提高开发效率，增强程序的可靠性，也便于分工合作和修改维护。

实例1：计算x的n次方

#include<iostream>
using namespace std;
double pow(int x,int n){
	double result=1;
	while(n){
	result*=x;
	n- -;		
}
	return result;
}
int main(){
	cout<<pow(5,2);
	return 0;
}

二、为什么要用函数重载
通常,自然语言中一个词可以有多个含义，如擦桌子，擦鞋，操作的方法可能不同，但没有人会说“请用擦桌子的方法擦桌子”，但人类从生活实践中学会了不同的“擦”的能力，能完全理解这样的语言，计算机会有同样的功能吗？

实例：实现两个整数的加法和两个浮点数的加法。

	#include<iostream>
	using namespace std;
	int add(int a,int b){
		return a+b;
	}
	float fadd(float a,float b){
		return a+b;
	}
	int main(){
		int a=5,b=3;
		float c=1.2,d=2.3;
		cout<<“a+b=”<<add(a,b)<<endl;
		cout<<“c+d=”<<add(c,d)<<endl;
	}

这样调用实在不方便。那么这个时候就能体现重载函数的好处了。

什么是重载函数：两个以上的函数，具有相同的函数名，但是形参的个数或者类型不同，编译器根据实参和形参的个数类型的最佳匹配，自动确定调用哪一个函数，这就是函数的重载。

实例：

	#include<iostream>
	using namespace std;
	int add(int a,int b){
		return a+b;
	}
	float add(float a,float b){
		return a+b;
	}
	int main(){
		int a=5,b=3;
		float c=1.2,d=2.3;
		cout<<“a+b=”<<add(a,b)<<endl;
		cout<<“c+d=”<<add(c,d)<<endl;
	}

c++允许功能相近的函数中相同的作用域内以相同函数名，从而实现重载，方便使用与记忆。

三、值传递与地址传递

值传递实例：

#include<iostream>
using namespace std;
void swap1(int x, int y)
{
	int tmp = x;
	x = y;
	y = tmp;
	cout << "x = " << x << ", y = " << y << endl;
}

void main()
{
	int a = 2, b = 7;
	swap1(a, b);
	cout << "a = " << a << ", b = " << b << endl;
}

运行结果：

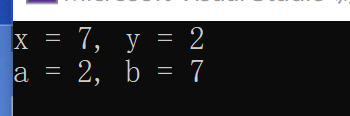
传值相当于在内存空间中开辟另外一块新内存并将值存入新内存空间，对其的改变不在原内存空间上进行，不影响原变量。

地址传递实例：

#include<iostream>
using namespace std;
void swap1(int* x, int* y)
{
	int tmp;
	tmp = *x;
	*x = *y;
	*y = tmp;
	cout << "x = " << *x << ", y = " << *y << endl;
}

void main()
{
	int a = 2, b = 7;
	swap1(&a, &b);
	cout << "a = " << a << ", b = " << b << endl;
}

运行结果：

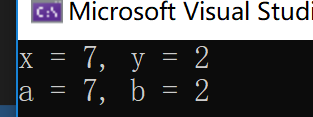
地址传递是将变量地址作为实参传入函数，函数内对变量的改变直接在原内存上进行

四、递归函数

函数可以直接或间接的调用自身，称为递归调用。

实例：计算n!

#include<iostream>
using namespace std;
int fuc(int n) {
	if (n == 1 || n == 0)return 1;
	else if (n < 0)return -1;
	else return n * fuc(n - 1);
}
int main() {
	int n = 4;
	cout << n << " != " << fuc(n) << endl;
}

运行结果：

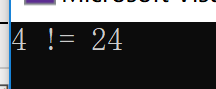
递归的过程有两个阶段：
1.递推。将原问题不断分解为新的子问题，逐渐从未知向推进，最终得到已知条件，此时递推结束。

例如:计算4！=>4*3!=>4*3*2!=>4*3*2*1;

2.回归。从已知条件出发，按照递推的逆过程，逐一求值回归。

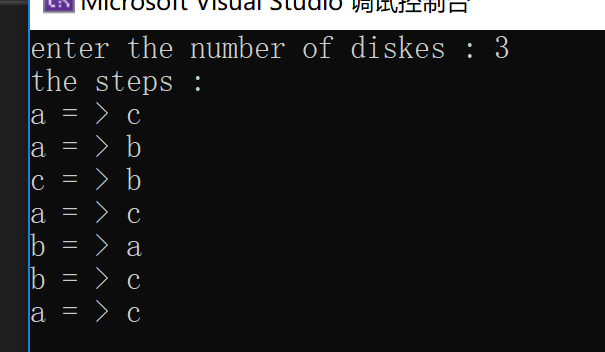
实例：汉诺塔问题。
有三根针a,b,c,a上有n个盘子，盘子大小不等，大的在下，小的在上，要求把这n个盘子从a移动到c，在移动过程中可以借助b，每次只允许移动一个盘子，且在三根针上都保持大的在下小的在上。

分析：将n个盘子a移动到c可分为三个步骤
1.把n-1个盘子移动到b上（以c为媒介）
2.把a上的一个盘子移动到c上
3.把b上的n-1个盘子移动到c上（以a为媒介）
 
其中1、3可理解为借助媒介把盘子从一根针移到另一根针上，因此可借助同一个函数hanoi实现
2用move函数实现

代码实现：

#include<iostream>
using namespace std;
void move(char src,char dest){ //src 最上的一个盘移向dest
	cout<<src<<“=>”<<dest<<endl;
}
void hanoi(int n,char src,char medium,char dest){
	if(n==1)
	move(src,dest);
	else{
		hanoi(n-1,src,dest,medium);//第一步
		move(src,dest);//第二步
		hanoi(n-1,medium,src,dest);//第三步
	}
}
int main(){
	int m;
	cout<<“enter the number of diskes:”;
	cin>>m;
	cout<<“the steps :”<<endl;
	hanoi(m,’a’,’b’,’c’);
	return 0;
}