Leetcode 5.最长回文子串

动态规划：

class Solution {
    public String longestPalindrome(String s) {
       int len=s.length();
        if(len==0)return s;
        boolean dp[][]=new boolean[len][len];//dp数组表示在两个下标之间的子串是不是回文串
        int maxLen=0;//记录最大长度
         String res=null;
         for (int i = len-1; i >=0; i--) {//因为dp依赖与中间的dp值，所以i从尾到头遍历
             for (int j = i; j < len; j++) {
                 //如果头尾两个值一样，并且头尾不是相邻时，依赖于中间dp值。
                 //中间如果只有一个字母，那必为回文，所以判断j-1<3
                 dp[i][j]=s.charAt(i)==s.charAt(j)&&(j-i<3||dp[i+1][j-1]);
                 //找最长
                 if(dp[i][j]&&(res==null||j-i>maxLen)){
                             res=s.substring(i,j+1);//此处可优化，只记录当前最小子串左右下标，最后在取子串
                             maxLen=j-i;
                     }
             }
         }
         return res;
    }
}

 压缩空间复杂度

 

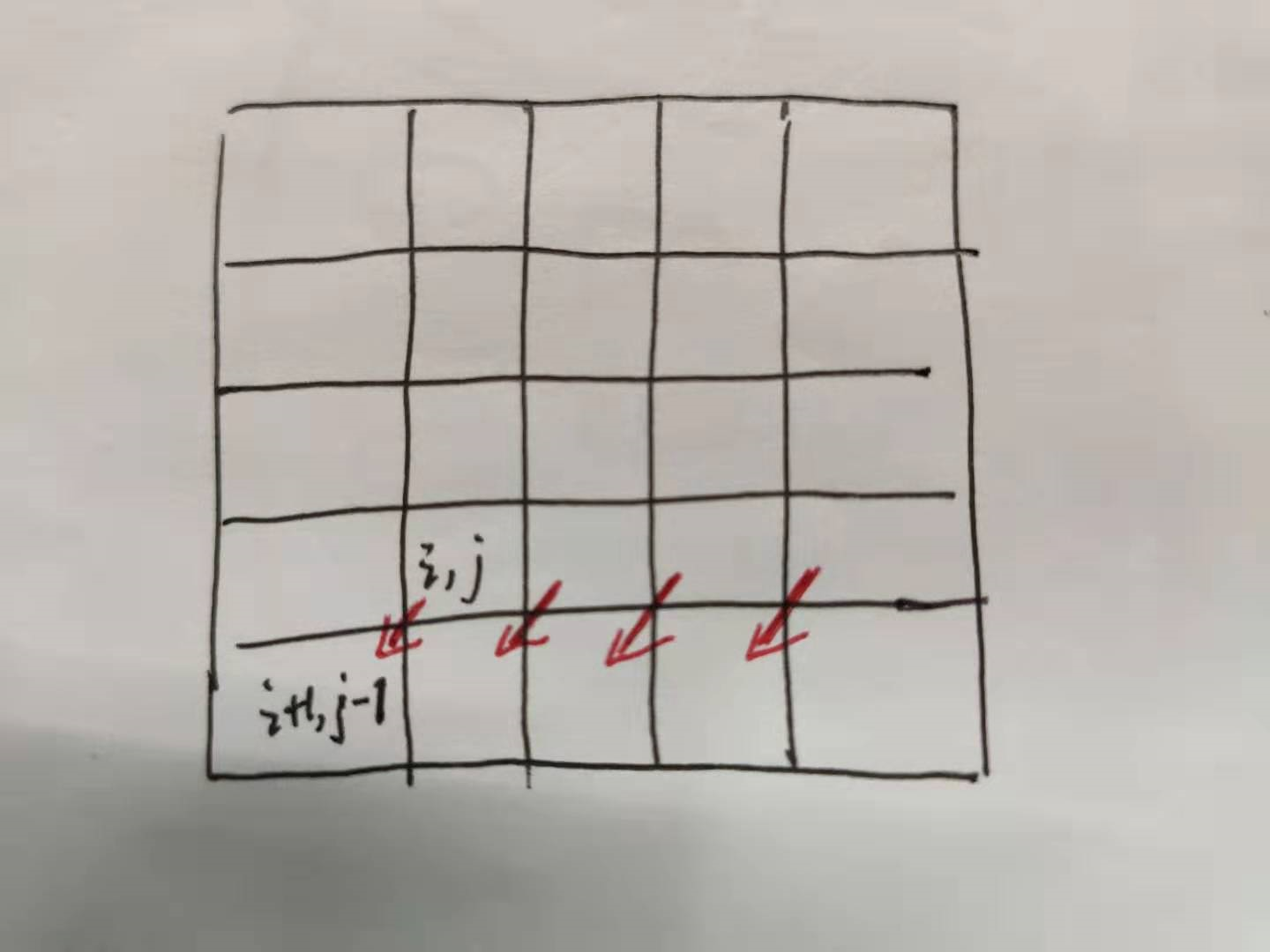
 相当于使用j-1位置的数据

故可以压缩空间

tmp=未更新值

更新值为前一个

prev=tmp

class Solution {
    public String longestPalindrome(String s) {
        if(s.length()==0)return "";
        boolean[] dp =new boolean[s.length()];
        int max_len=1;
        String res=s.substring(0,1);
        for (int i =  dp.length-1; i>=0; i--) {
            boolean prev=false;//注意prev是每次j的循环使用的共享变量
            for (int j=i;j<dp.length;j++){
                if(i==j){
                    dp[j]=true;
                }
                else if(j-i==1){
                    prev=dp[j];
                    dp[j]=(s.charAt(i)==s.charAt(j));
                }
                else if(i+1<dp.length&&j>0){
                    boolean tmp=dp[j];
                    if(s.charAt(i)==s.charAt(j)){
                        dp[j]=prev;
                    }
                    else {
                        dp[j]=false;
                    }
                    prev=tmp;
                }
                if(dp[j]&&j-i+1>max_len){
                    max_len=j-i+1;
                    res=s.substring(i,j+1);
                        }
            }
        }
        return res;
    }
}