二维柏林噪声

对于二维来说，要实现perlin噪声需要：

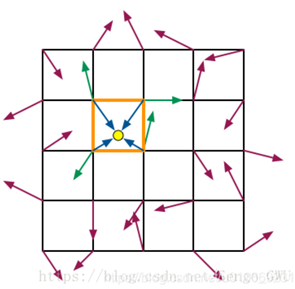
1.定义一个晶格结构（即一个平面网格，如上图），每个晶格的顶点有一个“伪随机”的梯度向量（说它是伪随机的是因为梯度向量是我们随机的选择我们自定义的向量得到的）。
2.输入一个点，我们找到和它相邻的那些晶格顶点（二维下有4个），得到该点到各个晶格顶点的向量，再分别与顶点上的梯度向量做点乘，得到4个点乘结果。
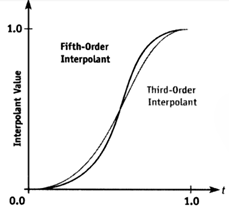
3.使用缓和曲线（ease curves）根据坐标来计算它们的权重和。老版的柏林噪声使用f(t)=3*t*t-2*t*t*t，改进后的柏林噪声使用f(t)=t*t*t*(t*(t*6-15)+10)，如下图。

• 对一个晶格顶点来说，其周围点的插值权重类似于高斯模糊，如下图。
  

• 对一个晶格顶点来说，它的梯度向量决定了它周围四块正方形中的点的其中一个点乘结果。这个点乘结果在它周围四块正方形中的分布也就被它的梯度向量决定了。这是一个围绕它呈同心圆向远处绝对值递增，绕关于它的梯度方向所在直线旋转后呈三角函数变化的分布。

所以二维柏林噪声是由晶格定点梯度方向决定的三角函数叠加上类高斯模糊。

考虑分型的柏林噪声
Perlin将不同倍程的噪声相加后的函数（每个噪声都比前一个倍程的噪声振幅减半）叫做1/f噪声，不过如今通常会使用分形布朗运动（fraction Brownian motion）或者fbm这个名词来描述它。
它考虑了分型的一部分，即层次间自相似性，没有考虑层次间的依赖关系。
分形见https://www.cnblogs.com/pigonthesea/p/14385852.html。