括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

方法一：深度优先遍历

我们以 n = 2 为例，画树形结构图。方法是 “做减法”。

 

 

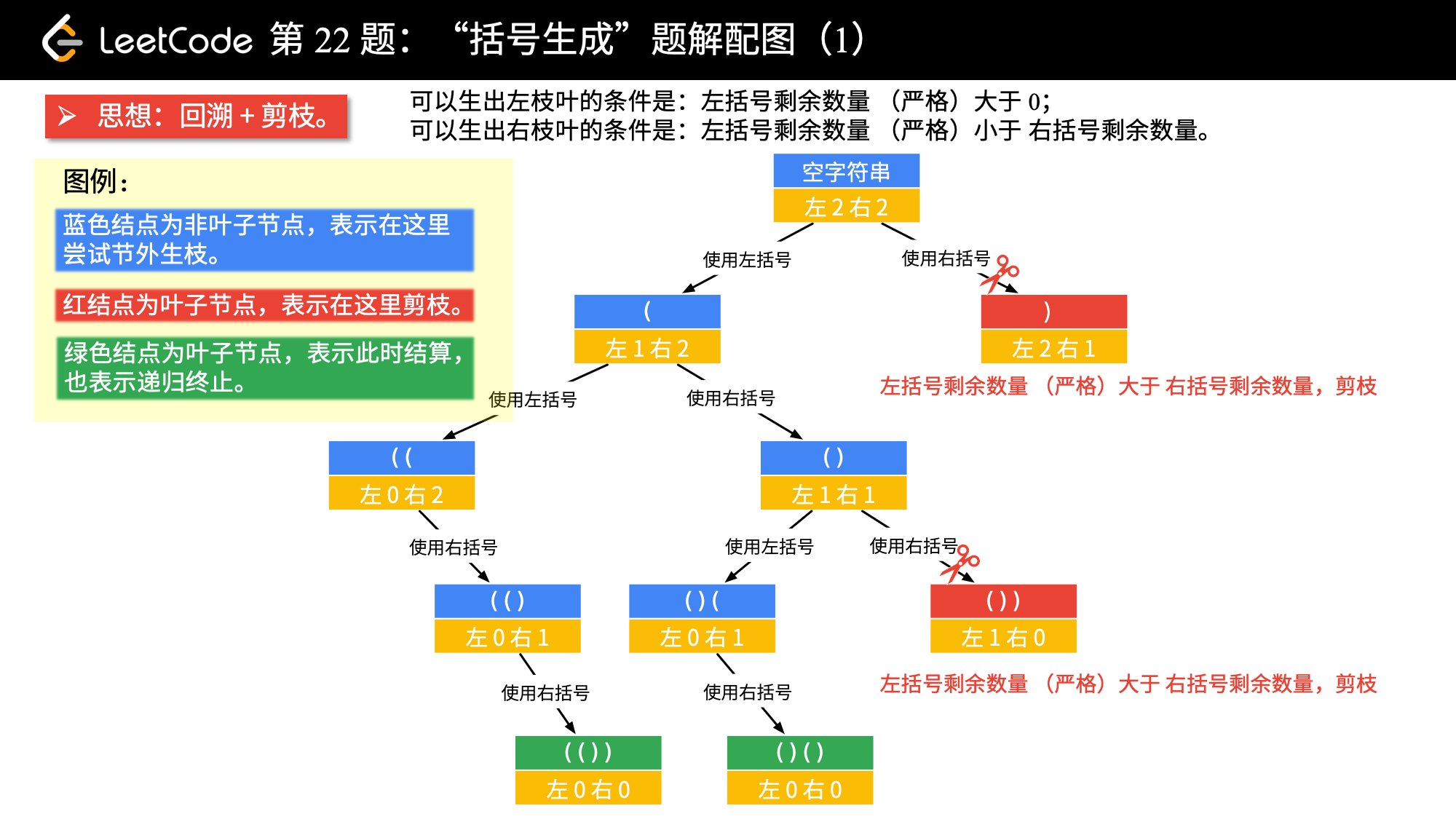
画图以后，可以分析出的结论：

    当前左右括号都有大于 000 个可以使用的时候，才产生分支；

    产生左分支的时候，只看当前是否还有左括号可以使用；

    产生右分支的时候，还受到左分支的限制，右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候，才可以产生分支；

    在左边和右边剩余的括号数都等于 000 的时候结算。

代码实现如下：

void generate(char *item,int index,int left,int right,char **result,int *count,int n)
 {
     if(left==0&&right==0)//已经全部插满了
        {
            result[(*count)]=(char*)malloc(sizeof(char)*(2*n+1));
            strcpy(result[(*count)++],item);
            return;
        }
        //result[(*count)++][]=item;
        item[index]='(';//插入左括号
        item[index+1]='\0';

        if(left>0)
        generate(item,index+1,left-1,right,result,count,n);
        if(right>left)//待插入右括号的个数多余待插入左括号的个数
        {
            item[index]=')';//插入右括号
            generate(item,index+1,left,right-1,result,count,n);
        }
 }
char ** generateParenthesis(int n, int* returnSize){
    int left=n,right=n;
    int length=2*2*n;
    int count=0;//记录已经插入的个数
    int index=0;//记录当前插入元素的下标

    char **result=(char **)malloc(sizeof(char *)*(5000));//创建二维数组
    char *item=(char *)malloc(sizeof(char)*(2*n+1));//创建存储数组

    generate(item,index,left,right,result,&count,n);
    *returnSize=count;

    return result;
}
这个是别人的代码，在力扣上可以跑过

如下是我的代码，不知道为什么跑步过去，但是在linux上编译调试都是可以的

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define MAX_STRINGS  1024

void dfs(char ***ret_strings, char * string, int index, int left, int right, int n, int * returnSize){
    char **strings=*ret_strings;
    if(left == 0 &&  right == 0){
        int count=*returnSize;
        if(count +1 >= MAX_STRINGS){
            strings=realloc(strings, malloc(sizeof(char *)*2*MAX_STRINGS));
            *ret_strings=strings;
            
        }
        string[index]='\0';
        strings[count]=malloc(sizeof(char)*(2*n+1));
        memset(strings[count], 0, sizeof(char)*(2*n+1));
        strcpy(strings[count], string);
        count++;
        *returnSize=count;
        return;
    }

    if(left > right){
        return;
    }

    if(left > 0){
        string[index]='(';
        dfs(ret_strings, string, index+1, left-1, right, n, returnSize);
    }

    if(right > 0){
        string[index]=')';
        dfs(ret_strings,string, index+1, left, right-1, n, returnSize);
    }

}

char ** generateParenthesis(int n, int* returnSize){
    int index=0;
    char ** ret_strings=NULL;
    char * string=NULL;
    ret_strings=malloc(sizeof(char *)*MAX_STRINGS);
    string=malloc(sizeof(char)*(2*n+1));
    dfs(&ret_strings, string,index, n, n, n,returnSize);
    return ret_strings;
}

int main(int argc, char ** argv){
    char ** ret_strings=NULL;
    int  num=0;
    ret_strings=generateParenthesis(atoi(argv[1]), &num);
    printf("[\n");
    int ii=0;
    for(;ii<num; ii++){
        printf("\t\"%s\",\n", ret_strings[ii]);
    }
    printf("]\n");

}

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/generate-parentheses/solution/hui-su-suan-fa-by-liweiwei1419/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/generate-parentheses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。