卡尔曼滤波器-初识

参考

入坑SLAM，前段时间在做相机标定，最近又用到了卡尔曼滤波器，不查不知道，原来这个玩意这么厉害，火箭都是靠它上天的！

阿波罗登月是"划着洗衣盆飘过大西洋"，那么这套估计理论大概就相当于洗衣盆上的那个舵手了。现在在航天领域，卡尔曼滤波是一种殿堂级的理论。

我没有学过控制类相关课程，临时抱佛脚学习一下。当然也仅限于最基本原理。

卡尔曼滤波器用来做什么？

简单来说，卡尔曼滤波器是用来得到对状态真实值的最优估计。
一个经典的例子是一台汽车在行进时，有多种方式获取行驶过的距离。可以通过当前速度等参数计算得到(这个不一定准确，因为会打滑，测量也有误差)；也可以通过激光雷达定位得到，这个也有误差；也可以通过计算机视觉SFM得到，也有误差。

虽然都有误差，但是这么多数据综合起来也许可能得到不错的结果吧。
综合计算和测量数值得到最优结果的方法，卡尔曼！

卡尔曼滤波器内容

前提条件前提是 小车的速度和位置量在其定义域内具有正态的高斯分布规律

还是以汽车行驶为例进行说明。
直观看对于行驶来说，关心的是距离，速度（毕竟对于车盲来说，其他也不知道了）。
我们的观察量是\(X = [p, v]\) 其中\(p\)是行驶距离，\(v\)是速度。

我们的问题是获取准确的观察量X

估计量计算

那么位移和速度之间有没有关系？
多少有点嘛，速度大，位移也可能会大，这个在不同情况下具体的相关度不一样。那么我们用协方差矩阵来衡量相关度。这个矩阵记为 \(P\)

至此，如果我们直接计算下一阶段的距离，加速度为\(a\)距离\(p_k\)为

\(p_k = p_{k-1} + \delta tv_{k-1} + \frac{1}{2}a\delta t^2\)

\(v_k = v_{k-1} + a\delta t\)

\(u\) 是控制量，\(B_k\)是控制矩阵，\(w_k\)是不确定干扰项
写成矩阵形式如下

\[\hat{x}_k = \left[ \begin{matrix} 1 & \delta t \\ 0 & 1 \end{matrix} \right] \hat{x}_{k-1} + \left[ \begin{matrix} \frac{\delta t^2}{2} \\ \delta t \end{matrix} \right]a = F_k\hat{x}_{k-1} + B_ku_k + w_k\]

协方差更新方程

\[P_k = F_kP_{k-1}F^T_k + Q_k \]

这个根据协方差公式推导一下即可，\(Q_k\)是误差

至此已经得到了估计量的计算方程.
先验估计\(\hat{x}_k\)取决于如下三部分：一部分是上一次的最优估计值（也就是上一轮卡尔曼滤波的结果），一部分是确定性的外界影响值，另一部分是环境当中不确定的干扰。

先验估计协方差矩阵\(P_k\)，首先是依据第\(k-1\)次卡尔曼估计（后验估计）的协方差矩阵进行递推，再与外界在这次更新中可能对系统造成的不确定的影响求和得到。

你需要休息一下

观察量计算

人们总是不能够完全信任自身的经验，也需要另外的一条途径来纠正潜在发生的错误或者是误差。

所以，我们很自然的想到在车身安装各类的传感器，比如速度传感器、位移传感器等等，以这些传感器的反馈作为纠正我们推断的依据。

传感器的输出值不一定就是我们创建的状态向量当中的元素，有时候需要进行一下简单的换算。即使是，有可能单位也不对应，所以，需要一个转换。这个转换就是矩阵\(H_k\)，在一些文献当中也被称作状态空间到观测空间的映射矩阵。

举个例子，比如汽车上的雷达测距，只能测量得到距离，不能得到速度的估计。这样就要依靠\(H\)矩阵来将这个转换.观测噪声的协方差矩阵\(R\)表示。如果多种测量仪器综合使用，z在这里就是矩阵，每一行代表一种仪器的测量结果。

\(\overrightarrow z_t=H_k\hat x_k+\overrightarrow v_k\)

观测向量\(\overrightarrow {z_k}\),服从高斯分布并且其平均值认为就是本次的量测值\((z_1,z_2)\)。

通过空间映射矩阵，依据我们先验估计值，在量测空间当中，传感器的测量值理想情况下应该是这样的：

\(\overrightarrow \mu_{expected}=H_k\hat x_k\)

\(\Sigma_{expected}=H_kP_kH_k^T\)

但是，传感器对系统某些状态的测量也会有偏差。系统在某一个状态下，会推断出一组理想值，在另一个状态下，会有另外一组理想值，而对应时刻传感器的测量值一定是无法和理想值保持完全吻合的。由于测量噪声的存在，不同的系统状态下，测量具有一定误差，呈现高斯分布.
但是这个高斯分布的最中心还是当前的测量值。所以，还需要一个观测噪声向量以及观测噪声协方差来衡量测量水平，我们将它们分别命名为\(v_k\)和\(R_k\)

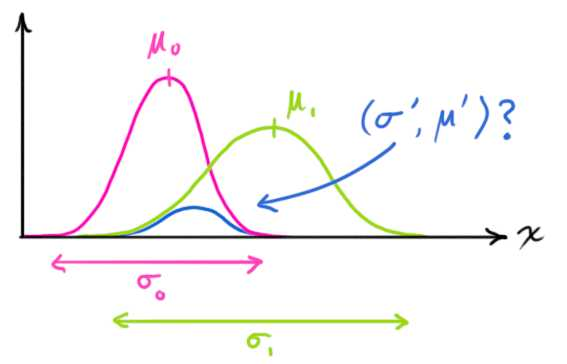
同时，我们也知道对于估计值和测量值两个分布他们重叠的部分，可能性更大

步骤

x是要得到的状态量，F是状态转移矩阵，P是观察量的协方差矩阵，B是控制矩阵，u是控制向量。Q是噪声协方差
H是转换矩阵，R是观测噪声协方差，K是卡尔曼增益

预测

\(\hat{x}^-_t = F\hat{x}_{t-1} + Bu_{t-1}\)

\(\hat{P}^-_t = F\hat{P}_{t-1}F^T + Q\)

更新

\(K_t = \hat{P}^-_tH^T(HP^-_tH^T(HP^-_tH^T + R)^{-1}\)

\(\hat{x}_t = \hat{x}^-_t + K_t(z_t - H\hat{x}^-_t)\)

\(P_t = (I - K_tH)P^-_t\)

所以发现卡尔曼程序只需要刚开始随机设置x,p(随即值不影响结果，几次迭代后就收敛了)，H，A，B都是事先设定的

参考

参考

参考