题解 CF903G Yet Another Maxflow Problem
Solution CF903G Yet Another Maxflow Problem
题意描述
给定一张图,左右各\(n\)个节点,\(A_i\to A_{i+1}\)连边,\(B_i\to B_{i+1}\)连边,容量给出。
有\(m\)对\(A_i\to B_j\)有边,容量给出。
你需要先求出原图从\(A_1\)到\(B_n\)的最大流,然后有\(q\)次操作,每次操作给出\(i\),先修改\(A_i\to A_{i+1}\)的边的容量,然后询问从\(A_1\)到\(B_n\)的最大流。
Solution:
显然最大流先转最小割,则考虑割掉哪些边最优。
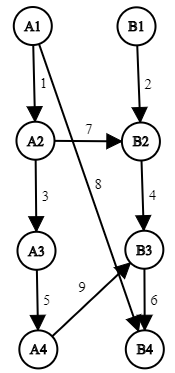
可以发现,割边有四种选择:左部链上割or不割,右部链上割or不割,乘法原理得到四种选择。
我们不希望过多的分类讨论,因此可以在\(A_1\)上面增加一条边表示左部不割边,在\(B_n\)下面增加一条边表示右部不割边。那么问题就是在左部割若干条边,右部割若干条边,再割掉中间与\(A_1,B_n\)连通的边,求所有方案最小代价。
在左部或右部同时割掉多条边显然是不优的,因为只有断掉的与\(A_1,B_n\)最近的边产生了割的效果,于是问题可以抽象为一个式子:
\[Min\{A_x+B_y+\sum\limits_{u,v\in E,u<x,v\geq y}W(u,v)\}
\]
此时回到题目:\(q\)次操作,每次操作给出\(i\),先修改\(A_i\to A_{i+1}\)的边的容量,然后询问从\(A_1\)到\(B_n\)的最大流。
注意到修改仅在左部进行,因此对于割掉一条左部边\(A_x\to A_{x+1}\),所对应的
\[B_y+\sum\limits_{u,v\in E,u<x,v\geq y}W(u,v)
\]
是不变的。考虑使用线段树,将\(B\)放到线段树上,从\(1\)到\(n\)加入\(A_x\),每到一个新点就枚举该点的边集\(E(x,v)\),在线段树上对应区间\(v\sim n\)进行区间加,然后求全局最小值。求完后将
\[Min\{A_x+B_y+\sum\limits_{u,v\in E,u<x,v\geq y}W(u,v)\}
\]
放入一棵新的线段树,之后的操作就是单点修改\(+\)全局最小值,直接维护即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
#define N 200005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
struct Edge{
int next,to,val;
}edge[N];
int n,m,q;
int head[N],num;
int A[N],B[N],res[N];
void add(int u,int v,int w){
edge[++num].next=head[u];
edge[num].to=v;
edge[num].val=w;
head[u]=num;
}
namespace SGT{
int Min[N<<2],Tag[N<<2];
void pushup(int k){Min[k]=min(Min[ls],Min[rs]);}
void pushdown(int k){
if(!Tag[k])return;
Min[ls]+=Tag[k];Min[rs]+=Tag[k];
Tag[ls]+=Tag[k];Tag[rs]+=Tag[k];
Tag[k]=0;
}
void build(int k,int l,int r){
Tag[k]=0;
if(l==r){
Min[k]=B[l];
return;
}
build(ls,l,mid);
build(rs,mid+1,r);
pushup(k);
}
void modify(int k,int l,int r,int x,int y,int val){
if(l>=x&&r<=y){
Min[k]+=val;
Tag[k]+=val;
return;
}
pushdown(k);
if(x<=mid)modify(ls,l,mid,x,y,val);
if(mid<y)modify(rs,mid+1,r,x,y,val);
pushup(k);
}
}
signed main(){
n=read();m=read();q=read();
for(int i=2;i<=n;i++)A[i-1]=read(),B[i]=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
add(u,v,w);
}
SGT::build(1,1,n);
for(int i=1;i<=n;i++){
for(int j=head[i];j;j=edge[j].next){
int v=edge[j].to,w=edge[j].val;
SGT::modify(1,1,n,1,v,w);
}
res[i]=SGT::Min[1];
}
for(int i=1;i<=n;i++)B[i]=res[i]+A[i];
SGT::build(1,1,n);
printf("%lld\n",SGT::Min[1]);
while(q--){
int x=read(),val=read();
SGT::modify(1,1,n,x,x,val-A[x]);
A[x]=val;
printf("%lld\n",SGT::Min[1]);
}
return 0;
}

