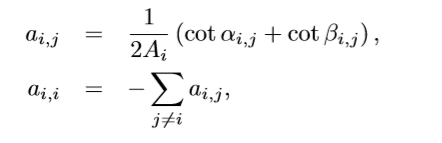数字几何处理(4)

参数化(parameterization)

　　建立一个三角网格曲面的参数化意味着找到一个坐标集合（u_i，v_i）与每一个顶点对应，坐标集合应该满足如下的条件：参数化之后的面不会自交。

几种不同的参数化方法：

　　重心映射( Barycentric Mapping)

　　　　重心映射是比较常见的三角网格参数化方法。给定一个三角网格曲面与圆盘(disk)同胚，如果边界顶点参数化之后的点连成一个凸多边形，内部顶点参数化之后的点是它1-邻域的顶点参数化之后坐标的凸组合，这样的参数化方法就是一种有效的参数化方法(不会自交)。

 

 

 

 

 　　拉普拉斯算子

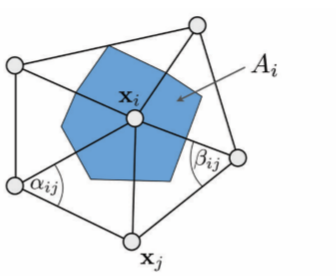
　　拉普拉斯算子衡量函数的规则性，例如，线性函数的；拉普拉斯算子为0，因此，极小化u,v的拉普拉斯算子可以得到光滑的参数化坐标，话句话说，极小化了参数化之后的扭曲。用离散微分几何的拉普拉斯算子可以计算a_i,j