排序算法--归并算法（强分治）

1,对比 弱分治归并算法 vs 强分治归并算法

 

弱分治：

 

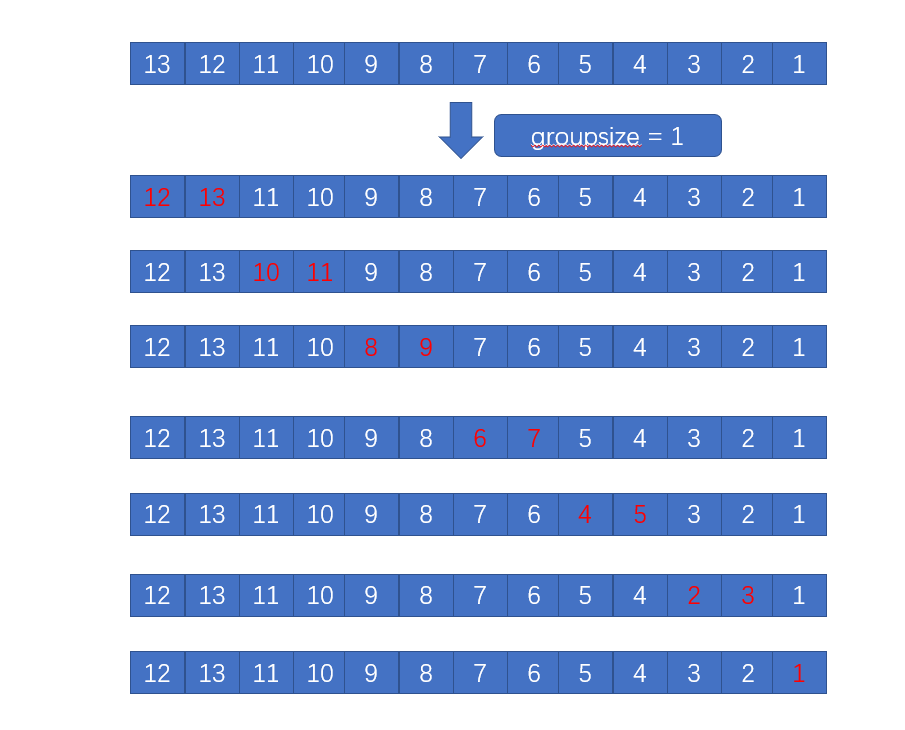
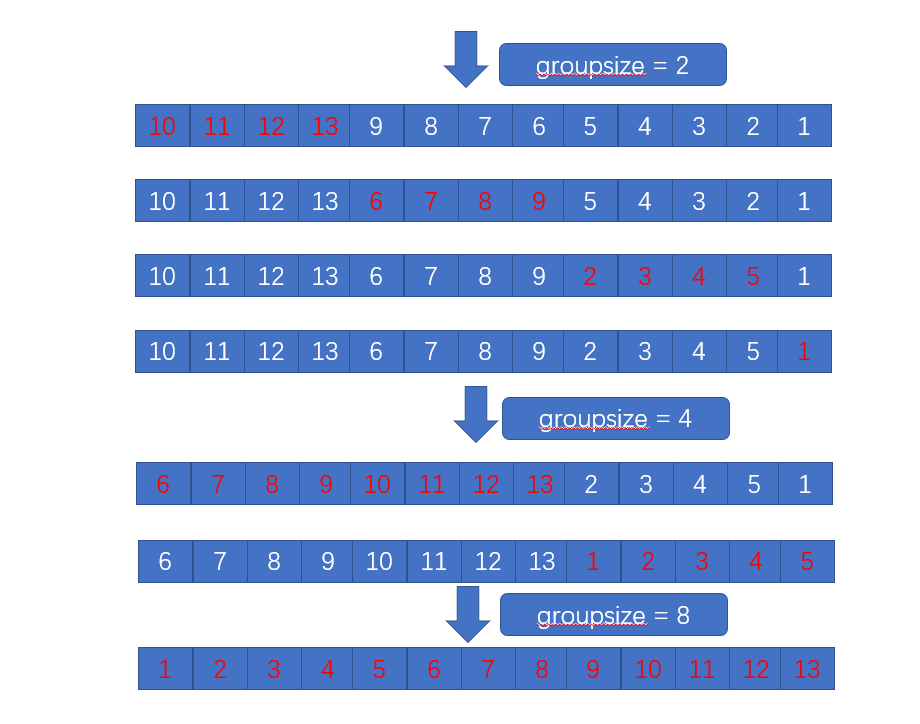
 强分治：

 

 

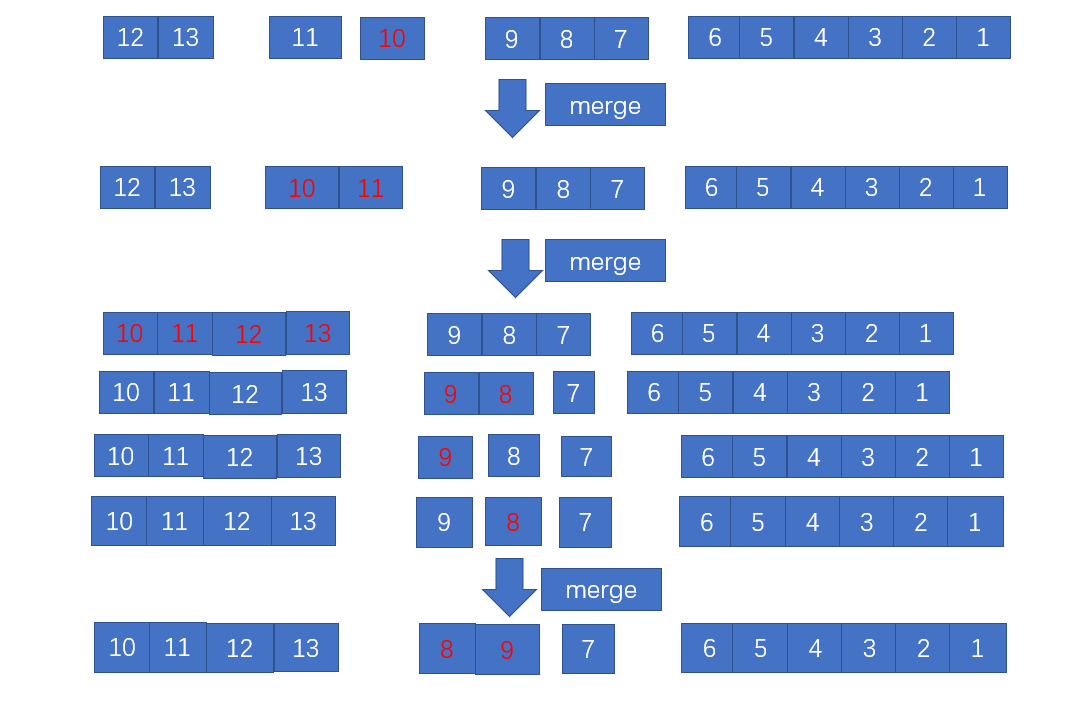
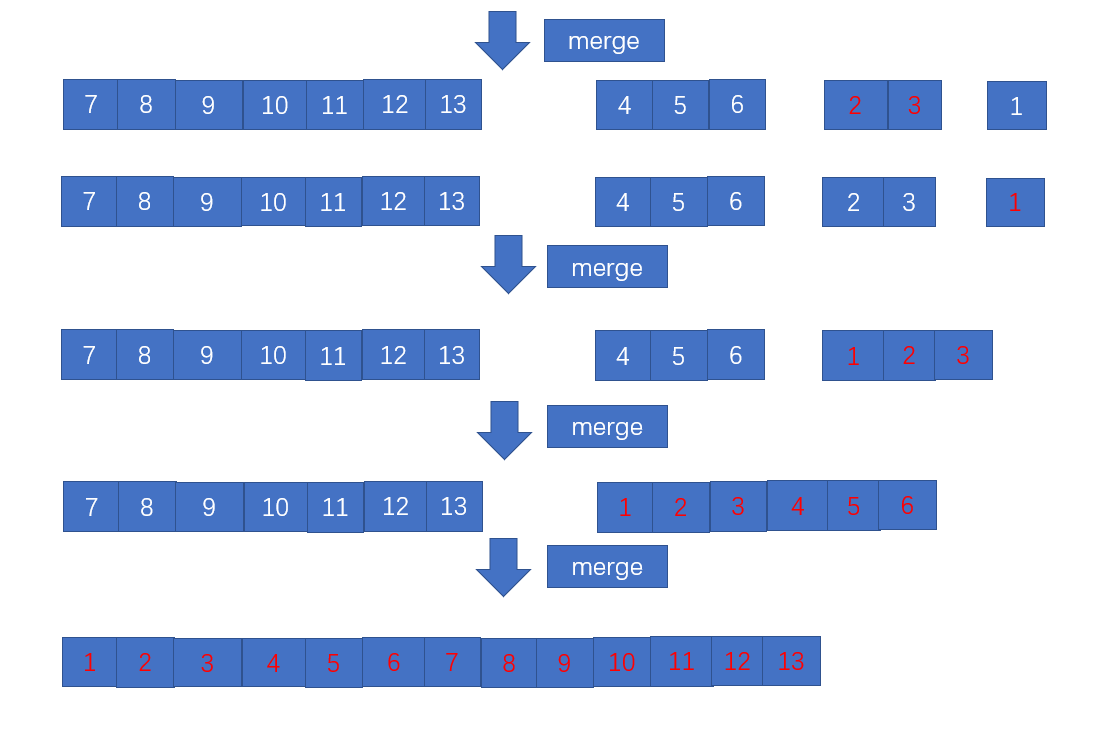
强分治归并排序与弱分治排序的归并逻辑是一致的，只是在分治逻辑不同，

是通过递归的方式，将源数列层层切割，以下标middlle 为分界点，切割的逻辑图如上所示，逐步切成成长度为1的有序数列，然后再层层反向归并。

代码参考如下：

 

 

public class MergeArray {

    public static void main(String[] args) {

        int[] nums = { 13, 12,11,10,9,8,7,6,5,4,3,2,1};  
        System.out.println(Arrays.toString(nums));  
        sort(nums, 0, nums.length-1);  
        System.out.println(Arrays.toString(nums));  
    }
      public static int[] sort(int[] nums, int low, int high){
            int mid = (low+high)/2;
            if(low<high){
                // 处理左边
                sort(nums, low, mid);
                // 处理右边
                sort(nums, mid+1, high);
                // 左右归并
                merge(nums, low, mid, high);
            }
            return nums;
        }

    private static void merge(int[] nums, int low, int mid, int high) {
        int[] temp = new int[high-low+1];
        int i = low;
        int j = mid+1;
        int k = 0;
        while(i<=mid && j<=high){
            if(nums[i]<nums[j])
                temp[k++] = nums[i++];
            else
                temp[k++] = nums[j++];
        }
        while(i<=mid){
            temp[k++] = nums[i++];
        }
        while(j<=high){
            temp[k++] = nums[j++];
        }
        for (int k2 = 0; k2 < temp.length; k2++) {
            nums[k2+low] = temp[k2];
        }
        System.out.println(Arrays.toString(nums));
    }

}

关于分治时候，用到的递归思想，请参照 https://www.cnblogs.com/pickKnow/p/9560410.html