狄克斯特拉算法

狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。

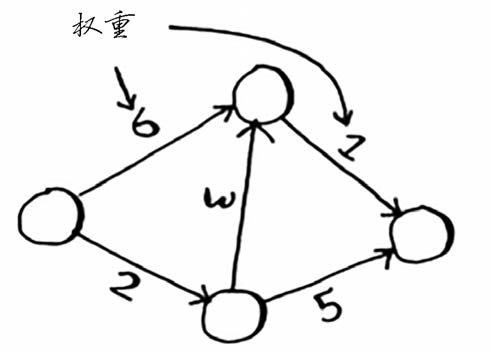
带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。

无向图意味着两个节点彼此指向对方，其实就是环！

在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。

例子：计算从起点到终点的用时最少的路径，以及时间

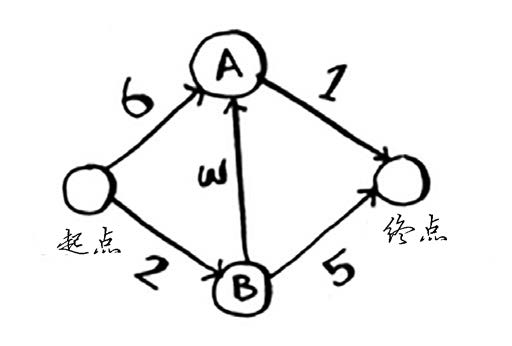
(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。
(2) 更新该节点的邻居的开销
(3) 重复这个过程，直到对图中的每个节点都这样做了。
(4) 计算最终路径。

 

节点的开销指的是从起点出发前往该节点需要多长时间。你知道的，从起

点到节点B需要2分钟，从起点到节点A需要6分钟（但你可能会找到所需时间更
短的路径）。你不知道到终点需要多长时间。对于还不知道的开销，你将其设
置为无穷大。在Python中能够表示无穷大吗？你可以这样做：infinity = float("inf")

第一步：

找出最便宜的节点。你站在起点，不知道该前往节点A还是前往节点B。前往这两
个节点都要多长时间呢？前往节点A需要6分钟，而前往节点B需要2分钟。至于前往

其他节点，你还不知道需要多长时间。由于你还不知道前往终点需要多长时间，

因此你假设为无穷大（这样做的原因你马上就会明白）。节点B是最近的——2分钟就能达到。

第二步：计算经节点B前往其各个邻居所需的时间。

对于节点B的邻居，如果找到前往它的更短路径，就更新其开销。在这里，你找到了：
 前往节点A的更短路径（时间从6分钟缩短到5分钟）；
 前往终点的更短路径（时间从无穷大缩短到7分钟）。

第三步：重复！
重复第一步：找出可在最短时间内前往的节点。你对节点B执行了第二步，除节点B外，可
在最短时间内前往的节点是节点A。

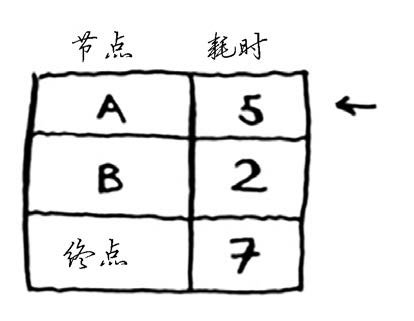
重复第二步：更新节点A的所有邻居的开销。

你发现前往终点的时间为6分钟！

你对每个节点都运行了狄克斯特拉算法（无需对终点这样做）。现在，你知道：

 前往节点B需要2分钟；

 前往节点A需要5分钟；

 前往终点需要6分钟。

 

需要：

创建开销表

一个存储父节点的散列表

一个数组，记录处理过的节点，对于同一个节点，你不用处理多次

 

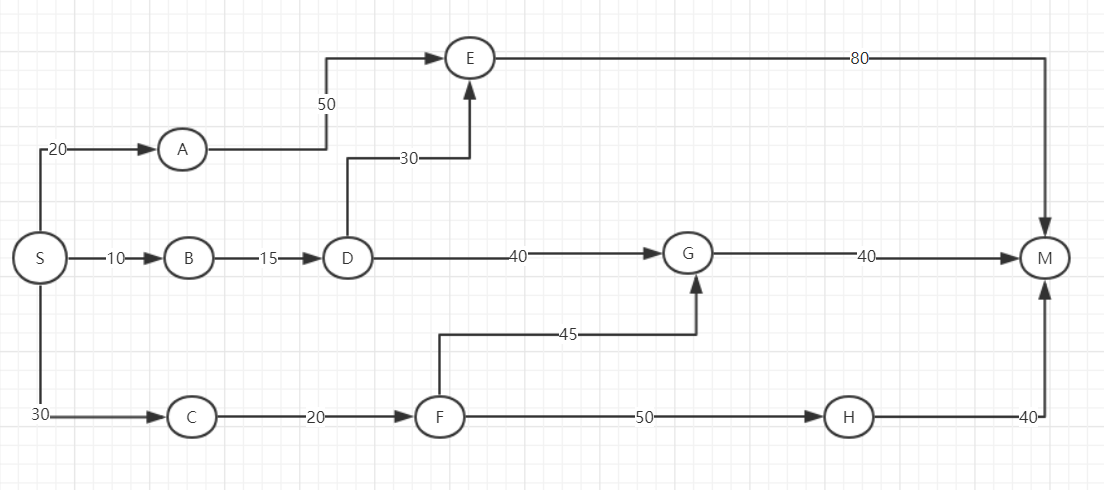
计算S城到M城的最短路径，边的权重表示分钟

 

# 建立图上节点的关系
graph={}
graph['S']={}   #node S
graph['S']['A']=20
graph['S']['B']=10
graph['S']['C']=30
graph['A']={}    #node A
graph['A']['E']=50
graph['B']={}    #node B
graph['B']['D']=15
graph['C']={}    #node C
graph['C']['F']=20
graph['E']={}    #node E
graph['E']['M']=80
graph['D']={}    #node D
graph['D']['E']=30
graph['D']['G']=40
graph['F']={}    #node F
graph['F']['G']=45
graph['F']['H']=50
graph['G']={}    #node G
graph['G']['M']=40
graph['H']={}    #node H
graph['H']['M']=40
graph['M']={}   #node M
# 建立开销表，即建立每个节点从初始点到节点的最短开销
infinity = float("inf") # 无穷
costs = {}
costs["A"] = 20
costs["B"] = 10
costs["D"] = 30
costs["E"] = infinity
costs["F"] = infinity
costs["G"] = infinity
costs["H"] = infinity
costs["M"] = infinity #未知即无穷
#存储每个节点开销最短的时候其父节点
parents = {}
parents["A"] = "S"
parents["B"] = "S"
parents["C"] = "S"
parents["E"] = None
parents["F"] = None
parents["G"] = None
parents["H"] = None
parents["M"] = None
#储存处理过的节点
processed = []

# 找到开销最小的点
def find_lowest_cost_node(costs):
    lowest_cost = float('inf')
    lowest_node = None
    for node in costs: # 遍历每个节点
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_node = node
    return lowest_node

#开始在遍历他的邻居的点，更新的他的临近的点的开销有没有跟新，比如A到D需要10min,A到B需要3min，B到D需要2min，那A到D的最短开销就要更新5min
node = find_lowest_cost_node(costs)
while node is not None:
    cost = costs[node] # 此节点的开销
    neibour = graph[node] # 获取这个节点的邻居
    # print(neibour)
    for neibour_node,neibour_value in neibour.items():
        # print(neibour_node)
        # print(neibour_value)
        new_cost = cost + neibour_value #邻居的开销，在开销的表中取比较并且更新
        if costs[neibour_node] > new_cost:
            costs[neibour_node] = new_cost
            parents[neibour_node] = node #把最低开销的作为邻居节点开销变小的父节点记录下来
    processed.append(node)
    node = find_lowest_cost_node(costs)



pre = parents['M']
path=['M'];
while(pre != 'S'):
    path.append(pre)
    pre = parents[pre]
path.append('S')
path.reverse()
print('最近的距离是：',costs['M'])
print('路线是：',path)

 

 广度优先搜索用于在非加权图中查找最短路径。
 狄克斯特拉算法用于在加权图中查找最短路径。
 仅当权重为正时狄克斯特拉算法才管用。
 如果图中包含负权边，请使用贝尔曼福德算法。