快速排序

快速排序的工作原理

1，从数组中选择一个元素，这个元素被称为基准值（pivot）。

2，接下来，找出比基准值小的元素以及比基准值大的元素。这被称为分区（partitioning）。

现在有：

 一个由所有小于基准值的数字组成的子数组；
 基准值；
 一个由所有大于基准值的数组组成的子数组。

3， 对这两个子数组进行快速排序。

4，两个子数组里面的元素

O(n log n)

def quick_sort(list):
    if len(list) < 2: # 基准条件,递归的终止条件
        return list
    else:
        pivot = list[0] # 设立基准值
        less = [i for i in list[1:] if i <= pivot] #小于等于基准值的放到一个列表
        greater = [j for j in list[1:] if j>= pivot] #大于等于基准值的放到一个列表
        return quick_sort(less) + [pivot] + quick_sort(greater) # 返回的一个个小的列表相加

var = quick_sort([8,2,5,3,1])
print(var) # [1, 2, 3, 5, 8]

快排涉及到D&C （分而治之），递归调用栈原理。

 

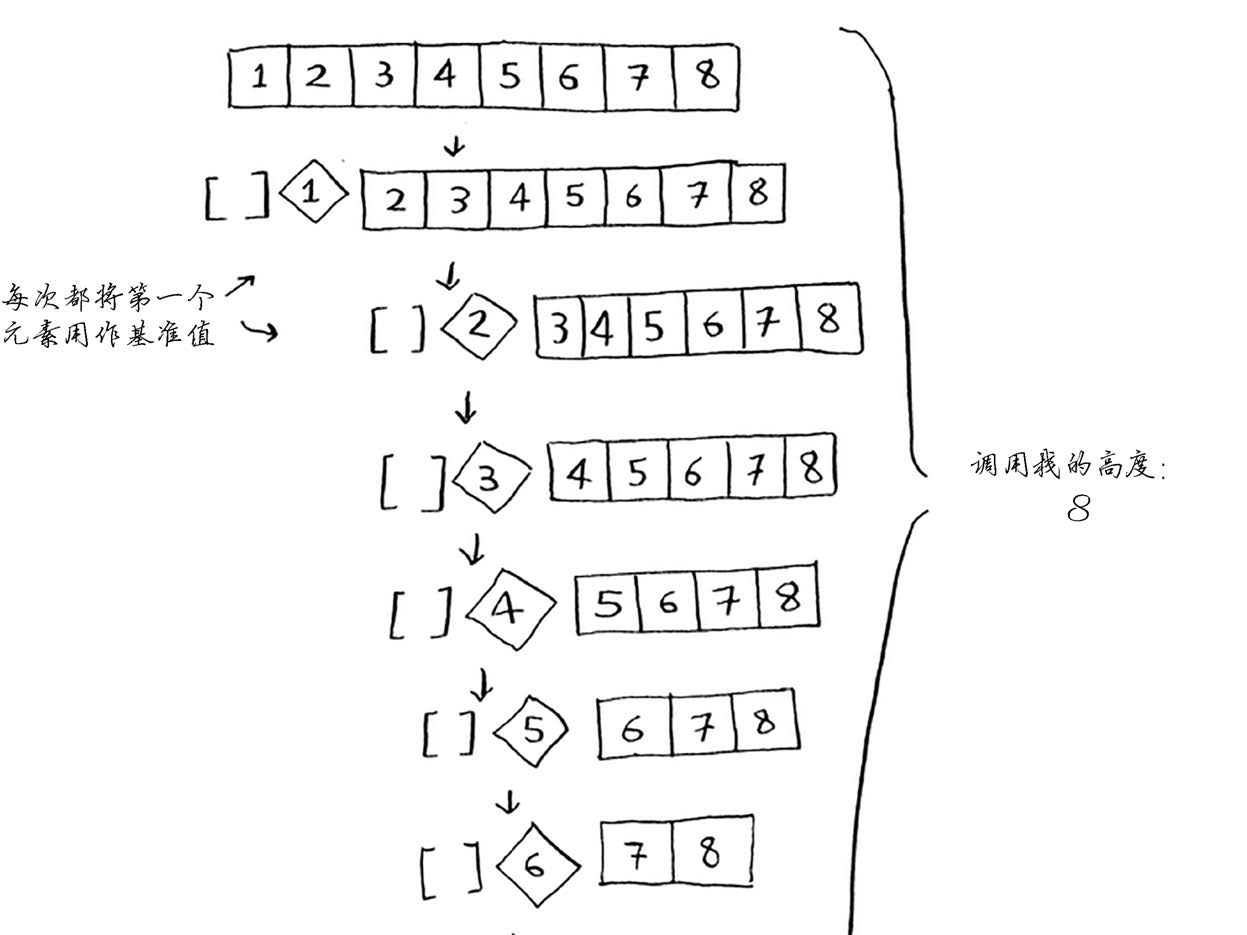
快速排序的性能高度依赖于你选择的基准值。假设你总是将第一个元素用作基准值，且要处
理的数组是有序的。由于快速排序算法不检查输入数组是否有序，因此它依然尝试对其进行排序。

 

 

注意，数组并没有被分成两半，相反，其中一个子数组始终为空，这导致调用栈非常长。现
在假设你总是将中间的元素用作基准值，在这种情况下，调用栈如下。

 

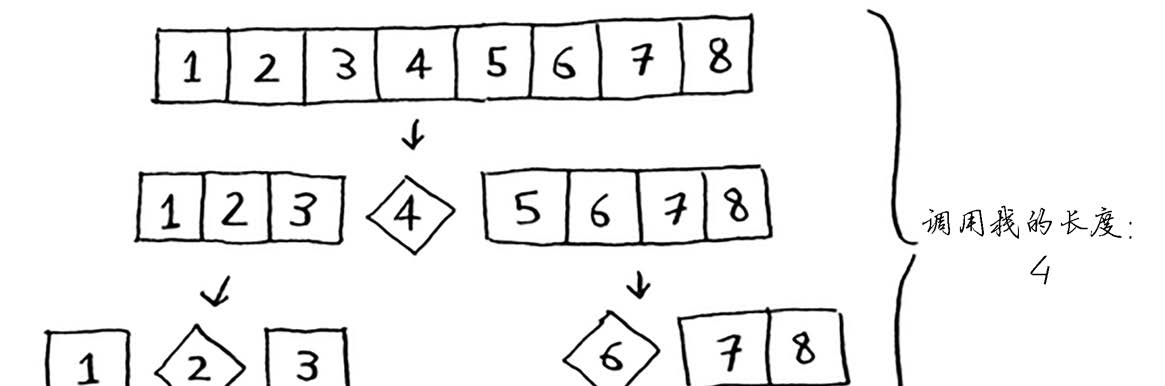
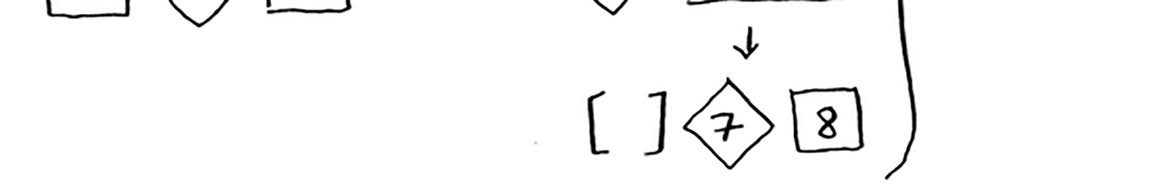
调用栈短得多！因为你每次都将数组分成两半，所以不需要那么多递归调用。你很快就到达
了基线条件，因此调用栈短得多。
第一个示例展示的是最糟情况，而第二个示例展示的是最佳情况。在最糟情况下，栈长为
O(n)，而在最佳情况下，栈长为O(log n)。
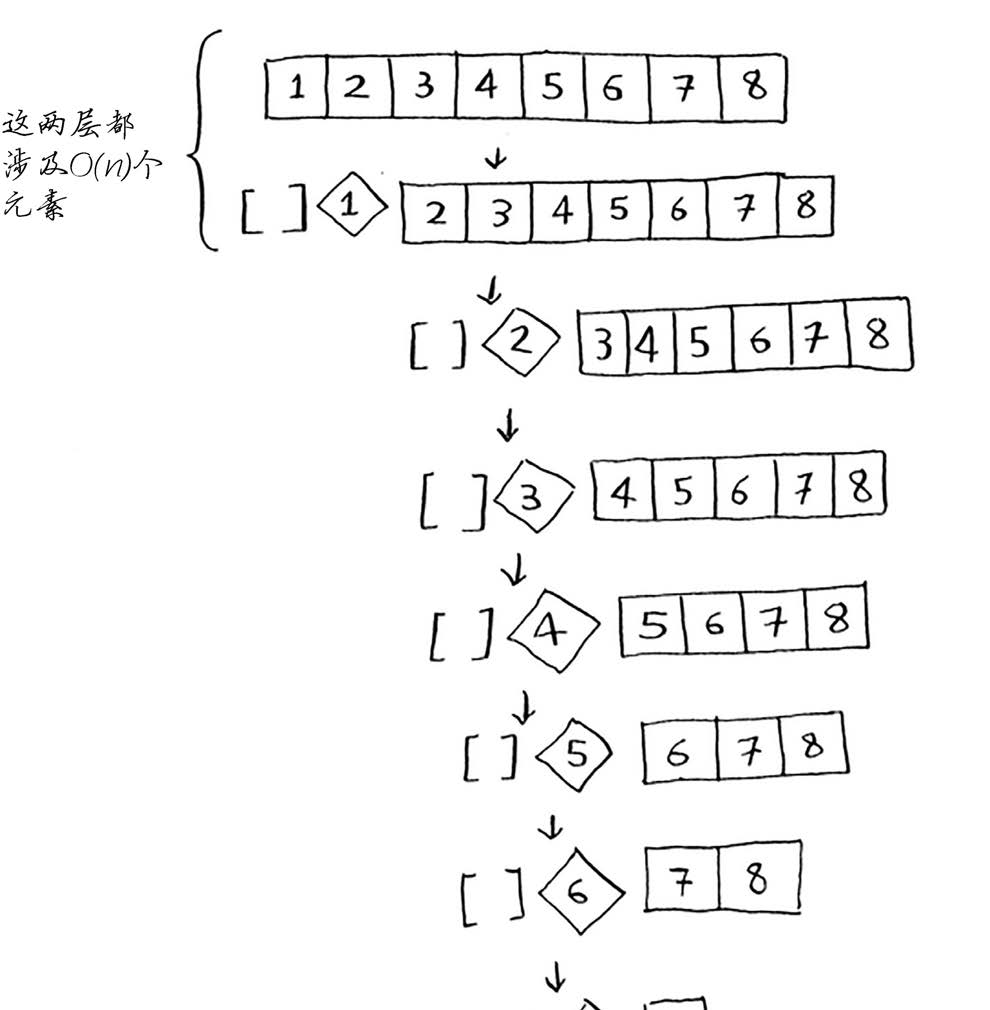
现在来看看栈的第一层。你将一个元素用作基准值，并将其他的元素划分到两个子数组中。
这涉及数组中的全部8个元素，因此该操作的时间为O(n)。在调用栈的第一层，涉及全部8个元素，
但实际上，在调用栈的每层都涉及O(n)个元素。

即便以不同的方式划分数组，每次也将涉及O(n)个元素。

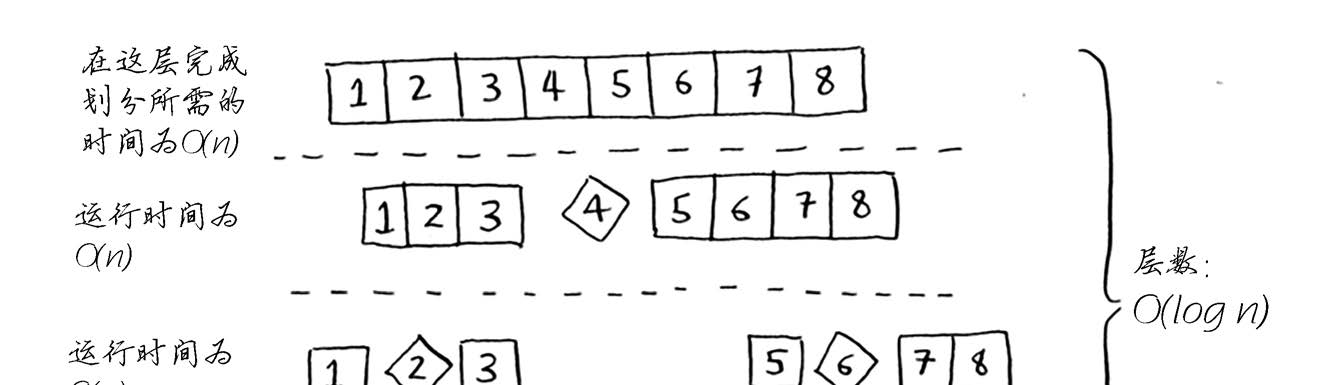
在这个示例中，层数为O(log n)（用技术术语说，调用栈的高度为O(log n)），而每层需要的
时间为O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。
在最糟情况下，有O(n)层，因此该算法的运行时间为O(n) * O(n) = O(n2)。
知道吗？这里要告诉你的是，最佳情况也是平均情况。只要你每次都随机地选择一个数组元
素作为基准值，快速排序的平均运行时间就将为O(n log n)。快速排序是最快的排序算法之一，也
是D&C典范。