决策树学习资料
分类决策树
- CSDN: 决策树（decision tree）(一)——构造决策树方法 (推荐)
- CSDN: 决策树（decision tree）(二)——剪枝 (推荐)
- CSDN: 决策树（decision tree）(三)——连续值处理 (推荐)
- CSDN: 决策树及决策树生成与剪枝
- 知乎：决策树——从零开始
- 知乎：决策树(Decision Tree)：通俗易懂之介绍
- 博客园：看完这篇--决策树，80%都懂了 （讲的不错，也有一点回归决策树的内容）
回归决策树
- CSDN 决策树-回归 （强烈推荐，讲解详细，有例子，清晰易懂）
- Regression Tree 回归树 （推荐，文中有很好例子详细说明怎么找每个变量的切分点）
回归树每个变量（特征）的切分点的寻找方法：遍历该特征的所有可能取值，把每个取值当做潜在的可能切分点，计算每个取值对应的均方差，均方差最小的那个取值作为切分点。这样的操作只是完成了一次切分，需要重复多次切分，直到满足一定的停止条件为止，比如节点中所有目标变量的值相同或者树的深度达到了预先指定的最大值等等。
GBDT中的树都是回归树，不是分类树。
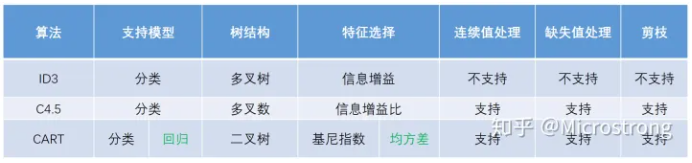
基础概念
决策树就是一棵树，一颗决策树包含一个根节点、若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点则对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集，从根结点到每个叶子结点的路径对应了一个判定测试序列。
决策树学习的关键在于如何选择最优的划分属性，所谓的最优划分属性，就是尽量使划分的样本属于同一类别，即“纯度”最高的属性。样本集的信息熵越小，纯度越高。
基尼指数反映了从数据集D中，随机抽取两个样本，这两个样本的类别不相同的概率。所以在候选属性集合中，选择那个使得划分后基尼指数最小的属性作为最优划分属性。
剪枝
剪枝（pruning）的目的是为了避免决策树模型的过拟合。因为决策树算法在学习的过程中为了尽可能的正确的分类训练样本，不停地对结点进行划分，因此这会导致整棵树的分支过多，也就导致了过拟合。决策树的剪枝策略最基本的有两种：预剪枝（pre-pruning）和后剪枝（post-pruning）：
- 预剪枝（pre-pruning）：预剪枝就是在构造决策树的过程中，先对每个结点在划分前进行估计，若果当前结点的划分不能带来决策树模型泛华性能的提升，则不对当前结点进行划分并且将当前结点标记为叶结点。
- 后剪枝（post-pruning）：后剪枝就是先把整颗决策树构造完毕，然后自底向上的对非叶结点进行考察，若将该结点对应的子树换为叶结点能够带来泛华性能的提升，则把该子树替换为叶结点。
预剪枝的优点：
- 降低了过拟合的风险；
- 减少了决策树的训练时间开销和测试时间开销。
预剪枝的缺点：因为预剪枝是基于“贪心”的，所以，虽然当前划分不能提升泛华性能，但是基于该划分的后续划分却有可能导致性能提升，因此预剪枝决策树有可能带来欠拟合的风险。
后剪枝决策树通常比预剪枝决策树保留了更多的分支，一般情形下，后剪枝决策树的欠拟合风险小，泛华性能往往也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的，并且要自底向上的对树中的所有非叶结点进行逐一考察，因此其训练时间开销要比未剪枝决策树和预剪枝决策树都大得多。
