先验概率和后验概率的理解；贝叶斯分类

理解先验概率和后验概率的时候，千万不要被中文翻译给误导了，直接看英文术语，更容易理解。

P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率，posterior probability。posterior的意思是：coming after in time，即在之后发生的。我们的关注目标是A，且A是在B发生之后发生的，所以P(A|B)叫做A的posterior probability。

P(A)是A的先验概率，prior probability。prior的意思是：happening or existing before sth else。先发生，所以叫prior probability，即A先发生，它不考虑任何B方面的因素。

 

贝叶斯法则：

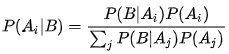
$P(B|A_i)$有时被称作似然度。贝叶斯法则可以概括为：后验概率 = (似然度 * 先验概率)/标准化常量，也就是说，后验概率与先验概率和似然度的乘积成正比。

 

概率$P(C_i|\bold{x})$是已知样本$\bold{x}$的情况下，求该样本属于$C_i$的概率，$C_i$发生在后面，所以叫做$C_i$的后验概率。

 

贝叶斯分类法的基本思想的是把计算后验概率的问题转化为计算先验概率的问题，如下图所示：

这篇博客有一个求后验概率的例子。

ps: 在李宏毅的教学视频中，$P(C_i)$叫做 prior probability，$P(\bold{x}|C_i)$叫做class-depencent probability。