Gabor滤波原理和matlab实现
1. 傅里叶变换的缺点
傅里叶变换的公式为
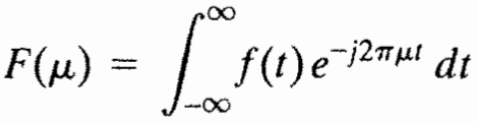
从公式中可以看出，傅里叶变换对信号在整个时域做了积分处理，因此其结果对时域信号在整个时间轴上进行了信息平均。这对于平稳信号来说是可行的，然而对于在时间上具有显著变化的非平稳信号来说，这样的做法显然不能满足我们对信号进行精确分析的要求。我们希望将信号分解到不同频率成分上来研究组成该信号的各频率成分的含量的同时，也能看到在信号的时变过程中，到底在哪一个时间段某一频率成分含量较多。（摘自2-D Gabor 滤波器特征提取）
2. Gabor变换
Gabor变换是D.Gabor 1946年提出的。为了由信号的傅里叶变换提取局部信息，引入了时间局部化的窗函数，得到了窗口傅里叶变换。由于窗口傅里叶变换只依赖于部分时间的信号，所以，现在窗口傅里叶变换又称为短时傅里叶变换。Gabor变换的基本思想：把信号划分成许多小的时间间隔，用傅里叶变换分析每一个时间间隔，以便确定信号在该时间间隔存在的频率。其处理方法是对 f(t)加一个滑动窗，再作傅里叶变换。Gabor变换所用的窗口函数是高斯函数，二维Gabor变换公式为(摘自Gabor滤波器学习)
参数含义：
λ：正弦函数波长，它的值以像素为单位指定，通常大于等于2，但不能大于输入图像尺寸的1/5.
θ：Gabor核函数(滤波器)的方向,这个参数指定了Gabor函数并行条纹的方向，他的取值为0到360度
ψ：相位偏移，调谐函数的相位偏移，取值-180到180。
σ：带宽，高斯函数的标准差，通常取2π
γ： 空间的宽高比，决定了Gabor函数形状的椭圆率，当γ=1时，形状是圆的，当γ<1时，形状随着平行条纹方向而拉长。通常该值为0.5
在特征提取方面，Gabor小波变换与其它方法相比：一方面其处理的数据量较少，能满足系统的实时性要求；另一方面，小波变换对光照变化不敏感，且能容忍一定程度的图像旋转和变形，当采用基于欧氏距离进行识别时，特征模式与待测特征不需要严格的对应，故能提高系统的鲁棒性。
3. 用matlab手动实现Gabor滤波器
代码：
clear;
ksize = 100; % kernel size
d = ksize/2;
lambda = 8; % wavelength
theta = 0; % orientation
phase = 0;
sigma = 8; % variation
ratio = 0.5; % spatial aspect ratio
g = zeros(ksize, ksize);
for x = 1:ksize
xd = x - d; % distance from the center
for y = 1:ksize
yd = y - d;
xn = xd*cos(theta) + yd*sin(theta);
yn = -xd*sin(theta) + yd*cos(theta);
g(x,y) = exp(-(xn^2+ratio^2*yn^2)/(2*sigma^2))*exp(1i*(2*pi*xn/lambda+phase));
end
end
subplot(121);
gReal = real(g);
gReal = gReal/sum(sum(gReal));
mesh(1:ksize,1:ksize,gReal);
title('real part');
xlabel('x');ylabel('y');
subplot(122);
gImag = imag(g);
gImag = gImag/sum(sum(gImag));
mesh(1:ksize,1:ksize,gImag);
title('imaginary part');
xlabel('x');ylabel('y');
运行结果：
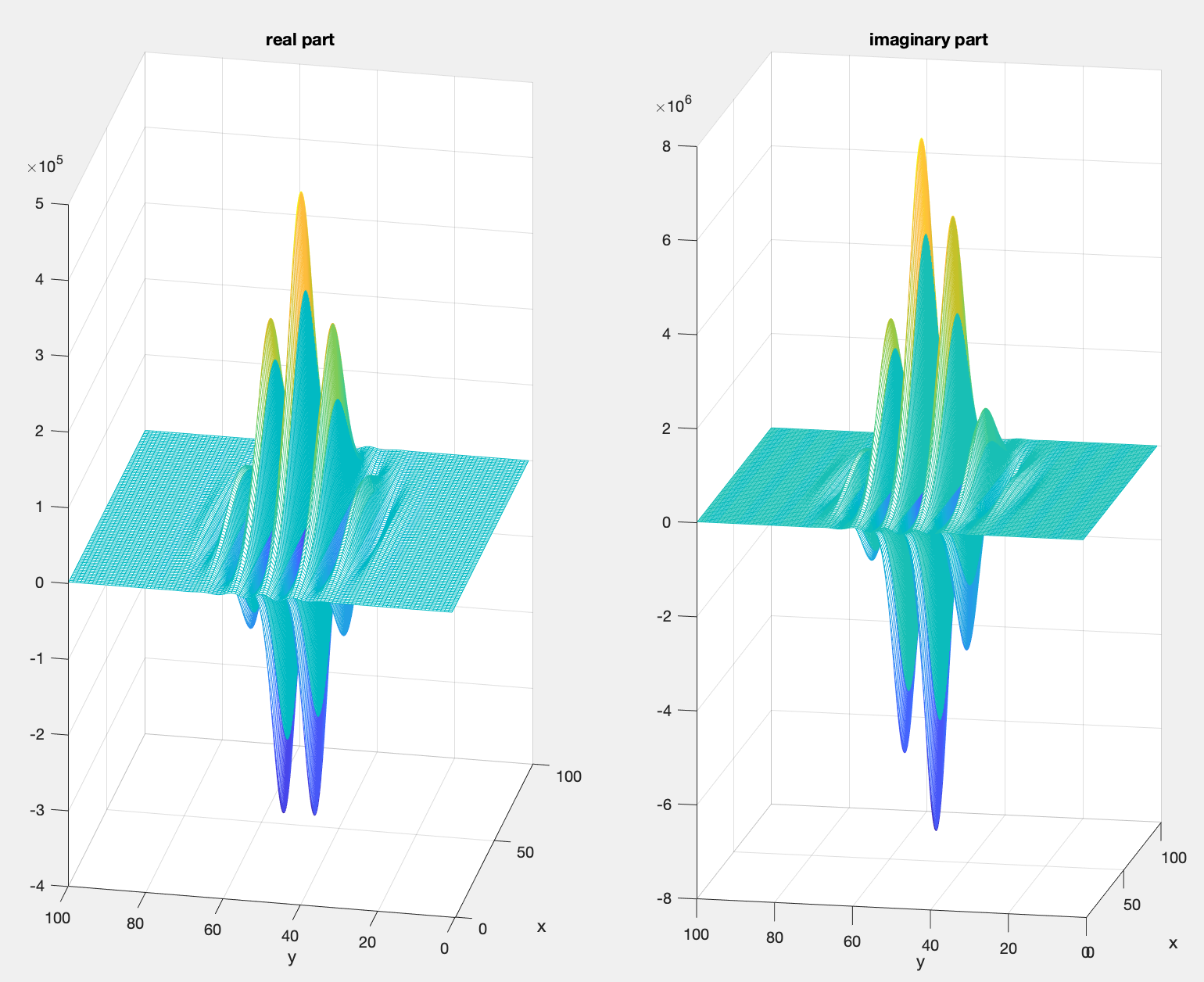
如果稍微转动一下图像，我们会发现，Gabor滤波其实就是一种小波变换（从公式上也能看出来）：
4. 用gabor滤波进行图像特征提取
gabor函数：
function g=gabor_func_peng(ksize,lambda,theta,phase,sigma,ratio)
% input
% ksize: kernel size
% lambda: wavelength
% theta: orientation
% phase: pahse angle
% sigma: variation
% ratio: spatial aspect ratio
% output
% g: gabor filter
d = ksize/2;
g = zeros(ksize, ksize);
for x = 1:ksize
xd = x - d; % distance from the center
for y = 1:ksize
yd = y - d;
xn = xd*cos(theta) + yd*sin(theta);
yn = -xd*sin(theta) + yd*cos(theta);
g(x,y) = exp(-(xn^2+ratio^2*yn^2)/(2*sigma^2))*exp(1i*(2*pi*xn/lambda+phase));
end
end
end
图像处理函数：
function Ig=gabor_imgProcess_peng(I,ksize,lambda,theta,phase,sigma,ratio)
% input
% I: input gray image
% ksize: kernel size
% lambda: wavelength
% theta: orientation
% phase: pahse angle
% sigma: variation
% ratio: spatial aspect ratio
% output
% g: gabor filter
[m,n] = size(I);
d = ksize/2;
% pad image
Ip = zeros(m+ksize, n+ksize);
Ip(d+1:d+m, d+1:d+n)=I;
g = gabor_func_peng(ksize,lambda,theta,phase,sigma,ratio);
g = real(g); % only use the real part of gabor filter
Ig = zeros(m,n);
disp('get gabor');
for x = 1:m
for y = 1:n
Ig(x,y) = sum(sum(Ip(x:x+ksize-1,y:y+ksize-1).*g));
end
end
Ig = uint8(Ig);
Ig = min(255, max(0, Ig));
主程序：
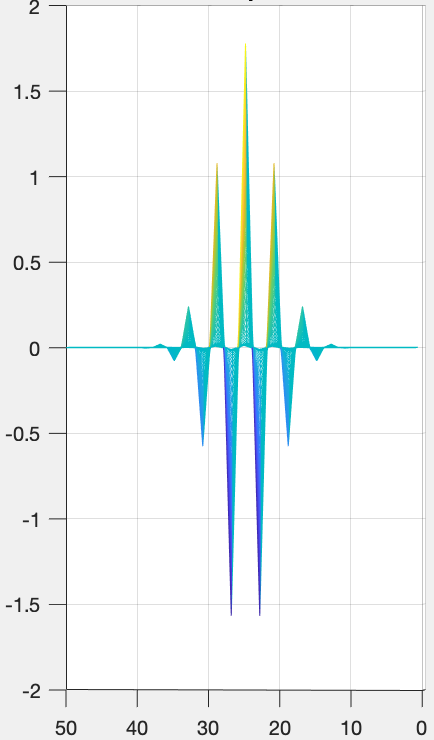
clear;
ksize = 50; % kernel size
d = ksize/2;
lambda = 6; % wavelength
theta = [0, pi/2]; % orientation
phase = 0;
sigma = 4; % variation
ratio = 0.5; % spatial aspect ratio
I = imread('../lena.jpg');
I = rgb2gray(I);
Ig_cell = cell(1,length(theta));
for k = 1:length(theta)
Ig_cell{1,k} = gabor_imgProcess_peng(I,ksize,lambda,theta(k),phase,sigma,ratio);
end
subplot(141);
imshow(I);title('original image');
subplot(142);
imshow(Ig_cell{1,1});title('gabor image, 0 degree');
subplot(143);
imshow(Ig_cell{1,2});title('gabor image, 90 degree');
subplot(144);
imshow(Ig_cell{1,1}+Ig_cell{1,2});title('gabor image, 0 and 90 degree');
运行结果：
参考资料
[1] 代码参考了手动实现Gabor滤波器
[2] Gabor滤波的公式讲解以及Python实现可参考油管视频What are Gabor filters?
[3] Gabor滤波
