降维和聚类系列(二)：拉普拉斯特征映射Laplacian Eigenmaps，谱聚类，实例代码

1. 邻接矩阵，度矩阵，拉普拉斯矩阵

给定一个无向图：

我们可以用邻接矩阵(Adjacent Matrix)表示它：

把这个邻接矩阵记为W，W中的1表示有连接，0表示没有连接，例如第一行第二列的1表示图的节点1和节点2有连接，第一行第三列的0表示图的节点1和节点3没有连接在一起。因为是无向图，所以W是对称矩阵。

我们把W中的每一行相加，放到对角线上，然后把对角线以外的元素填0，得到度矩阵(Degree Matrix)：

把度矩阵记为D，则

$\mathrm{D}_{i j}=\left\{\begin{array}{l}\sum_{j=1}^{n} w_{ij}, i=j \\ 0, i \neq j\end{array}\right.$

$D_{ii}$表示了第i个节点的度，反映了这个节点的重要性。

拉普拉斯矩阵(Laplacian Matrix)定义为L=D-W：

2. 把数据样本构建成图

给定样本$x_1,x_2,...,x_n$，把这些样本看作图的一个个节点，那我们怎么把这些样本节点用边连接起来呢，哪些节点之间要有边，哪些节点之间不需要有边？因为拉普拉斯特征映射的核心思想是只保持局部的几何结构不变，所以我们只需要把节点与其周围若干个节点连接就可以，有下面2种较常用的选节点方法：

$\varepsilon$-neighborhoods: 如果样本$x_i$和$x_j$距离小于$\varepsilon$, 就把样本$x_i$和$x_j$用边连接起来。
k-nearest neighbors: 样本$x_i$只连接与它距离最近的k个样本。

连接起来之后，我们需要给边赋权重，有以下两种常用方法：

Heat Kernel:

$\mathrm{W}_{i j}=\left\{\begin{array}\\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{t}\right), if\ x_i\ and\ x_j\ are\ connected \\ 0, otherwise \end{array}\right.$

simple-minded: ($t \rightarrow \inf$)

$\mathrm{W}_{i j}=\left\{\begin{array} {}1, if\ x_i\ and\ x_j\ are\ connected \\ 0, otherwise \end{array}\right.$

在上一小节中的邻接矩阵W用的是simple-minded方法。

3. The unnormalized graph Laplacian

关于性质1，李宏毅机器学习教学视频semi-supervise视频的50:16~58:36这段里有讲到一个实际例子：

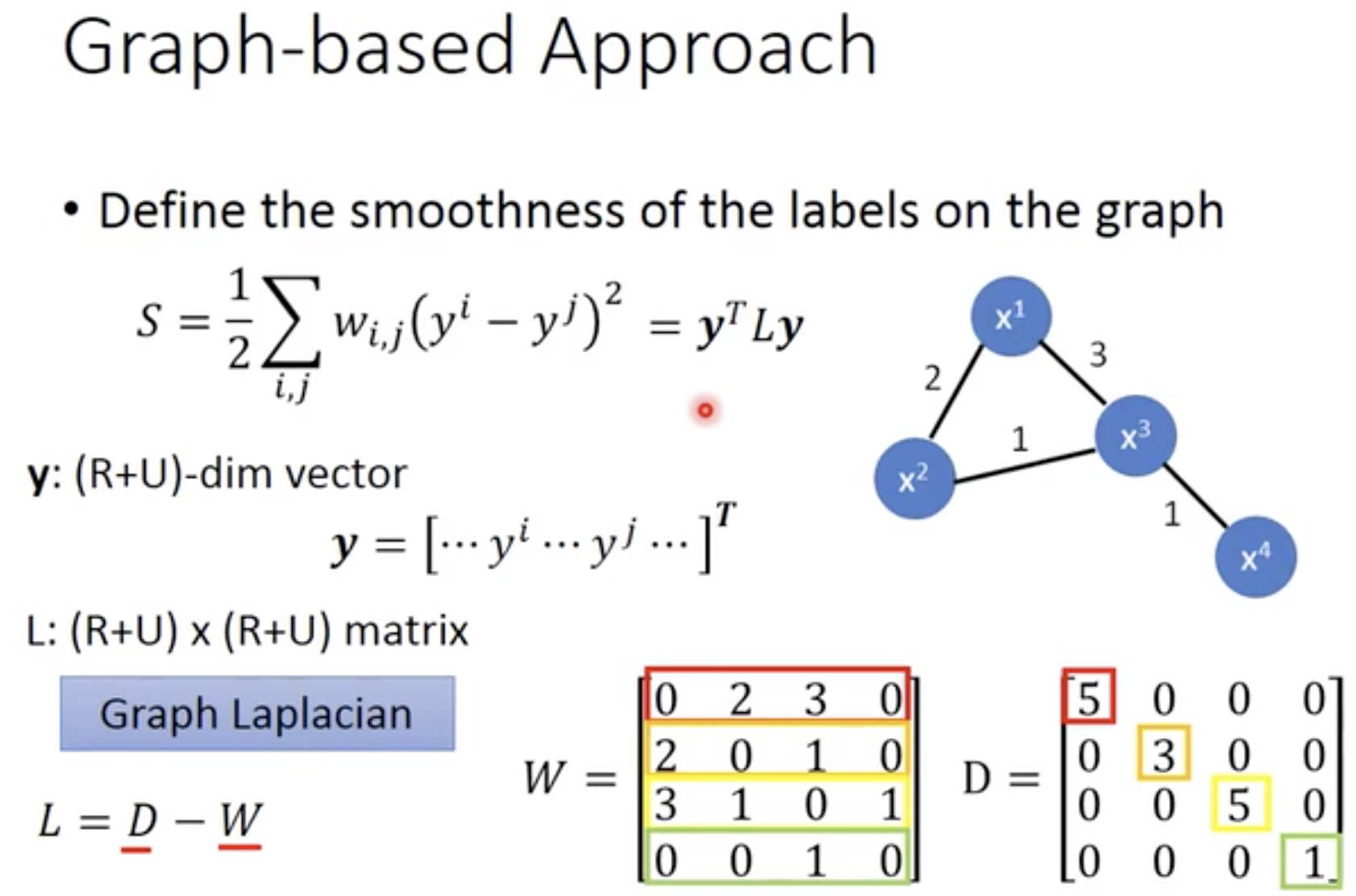
如果n=3，也就是只有3个节点，也可以直接把公式展开，各项消消掉，合并同类项等，就能比较清楚地知道上述的性质1是成立的：

4. The normalized graph Laplacian

5. The Algorithm

输入样本$x_1,x_2,...,x_n$，聚类数目k

根据第2节的方法构建邻接矩阵W，根据第1小节的方法构建度矩阵D；
根据第3或4小节的方法构建拉普拉斯矩阵L；
求解广义特征值问题：$L f=\lambda D f$；
把特征值从小到大排列为$\lambda_0,\lambda_1, \lambda_2...,\lambda_n$, 对应的特征向量为$f_0, f_1, f_2, ..., f_n$，其中最小的特征值$\lambda_0=0$，它对应的特征向量$f_0$是一个元素全为1的向量；
把$f_1, f_2, ..., f_k$这k个特征向量按列排列，形成大小为n*k的矩阵U；
把U的行记为$y_i (i=1,2,..,n)$，$y_i$就是样本$x_i$从高维空间映射大k维空间后的坐标，即$y_i$是$x_i$的embedding。
对$y_i (i=1,2,..,n)$进行聚类，比如用k-means进行聚类。$y_i$的聚类结果就是$x_i$的聚类结果。

(注：1. 很多文献中提到的相似度矩阵(similarity matrix)应该就是邻接矩阵。2. 谱聚类算法有很多种变体，这里叙述的只是其中一种)

6. Why This Algorithm works

拉普拉斯特征映射只考虑保持局部特征映射，因此一个自然的想法是，原高维空间中距离较近的样本$x_i$和$x_j$，映射为$y_i$和$y_j$，那么$y_i$和$y_j$的距离也应该比较接近，因此有人提出如下的目标函数：

$minimize\sum_{i=1}^{n} \sum_{j=1}^{n} (f_{i}-f_{j})^{2} W_{i j}$

如果$x_i$和$x_j$距离较近，则$W_{i j}$较大，这个时候如果$y_i$和$y_j$距离较远，则目标函数就会很大，因此最小化目标函数可以让$y_i$和$y_j$距离接近。

根据第三节的公式，有$\sum_{i=1}^{n} \sum_{j=1}^{n} (f_{i}-f_{j})^{2} W_{i j}=f^T W f$, 所以我们的目标函数可转化为

$minimize f^T L f, s.t. f^T D f=1$

约束是为了防止向量f的任意缩放。

用拉格朗日乘子法把有约束优化问题转化为无约束优化问题：

$minimize f^T L f + \lambda f^T D f$

函数对f求偏导，令该偏导为0，得到$(L-\lambda D)f=0$，即$Lf=\lambda D f$

7. 实例

下面的程序来自：https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LE

该程序中有两个laplacian eigenmaps的例子，第一个是把三维的swiss roll拉平成2维，第二个例子是把64维的手写数字样本降成2维。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from mpl_toolkits.mplot3d import Axes3D

'''
author: heucoder
email: 812860165@qq.com
date: 2019.6.13
'''

def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):
    #Generate a swiss roll dataset.
    t = 1.5 * np.pi * (1 + 2 * np.random.rand(1, n_samples))
    x = t * np.cos(t)
    y = 83 * np.random.rand(1, n_samples)
    z = t * np.sin(t)
    X = np.concatenate((x, y, z))
    X += noise * np.random.randn(3, n_samples)
    X = X.T
    t = np.squeeze(t)
    return X, t

def rbf(dist, t = 1.0):
    '''
    rbf kernel function
    '''
    return np.exp(-(dist/t))

def cal_pairwise_dist(x):
    '''
    计算pairwise 距离, x是matrix
    (a-b)^2 = a^2 + b^2 - 2*a*b
    '''
    sum_x = np.sum(np.square(x), 1)   # np.square(x)把矩阵x中的每个元素都各自平方
    dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
    #返回任意两个点之间距离的平方
    return dist

def cal_rbf_dist(data, n_neighbors = 10, t = 1):

    dist = cal_pairwise_dist(data)
    dist[dist < 0] = 0
    n = dist.shape[0]
    rbf_dist = rbf(dist, t)

    W = np.zeros((n, n))
    for i in range(n):
        index_ = np.argsort(dist[i])[1:1+n_neighbors]
        W[i, index_] = rbf_dist[i, index_]
        W[index_, i] = rbf_dist[index_, i]
    return W

def le(data, n_dims = 2, n_neighbors = 5, t = 1):
    '''
    :param data: (n_samples, n_features)
    :param n_dims: target dim
    :param n_neighbors: k nearest neighbors
    :param t: a param for rbf
    :return:
    '''
    N = data.shape[0]
    W = cal_rbf_dist(data, n_neighbors, t)   # 邻接矩阵
    D = np.zeros_like(W)   # 度矩阵
    for i in range(N):
        D[i, i] = np.sum(W[i])

    D_inv = np.linalg.inv(D)
    L = D - W
    eig_val, eig_vec = np.linalg.eig(np.dot(D_inv, L))
    sort_index_ = np.argsort(eig_val)
    eig_val = eig_val[sort_index_]
    print("eig_val[:10]: ", eig_val[:10])

    j = 0
    while eig_val[j] < 1e-6:
        j += 1
    print("j: ", j)

    sort_index_ = sort_index_[j:j+n_dims]   # 舍弃小于1e-6的特征值对应的特征向量
    eig_val_picked = eig_val[j:j+n_dims]
    print(eig_val_picked)
    eig_vec_picked = eig_vec[:, sort_index_]
    X_ndim = eig_vec_picked
    return X_ndim

if __name__ == '__main__':

    # example 1: swiss roll
    X, Y = make_swiss_roll(n_samples=2000)
    X_ndim = le(X, n_neighbors=5, t=20)

    fig = plt.figure(figsize=(12, 6))
    ax1 = fig.add_subplot(121, projection='3d')
    ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=Y)

    ax2 = fig.add_subplot(122)
    ax2.scatter(X_ndim[:, 0], X_ndim[:, 1], c=Y)
    plt.show()

    # example 2: hand-written digits
    # X = load_digits().data
    # y = load_digits().target
    # 
    # dist = cal_pairwise_dist(X)
    # max_dist = np.max(dist)
    # print("max_dist", max_dist)
    # X_ndim = le(X, n_neighbors=20, t=max_dist*0.1)
    # plt.scatter(X_ndim[:, 0], X_ndim[:, 1], c=y)
    # plt.savefig("LE2.png")
    # plt.show()

运行结果：

swiss roll: