矩阵微分系列二：矩阵迹求导
「本文部分内容摘自一份佚名的资料」
-------------------------------------------------------------------------------------------------------------------------------
符号说明：
1 -------------------------------------------------------------------------------------------------------------------------------
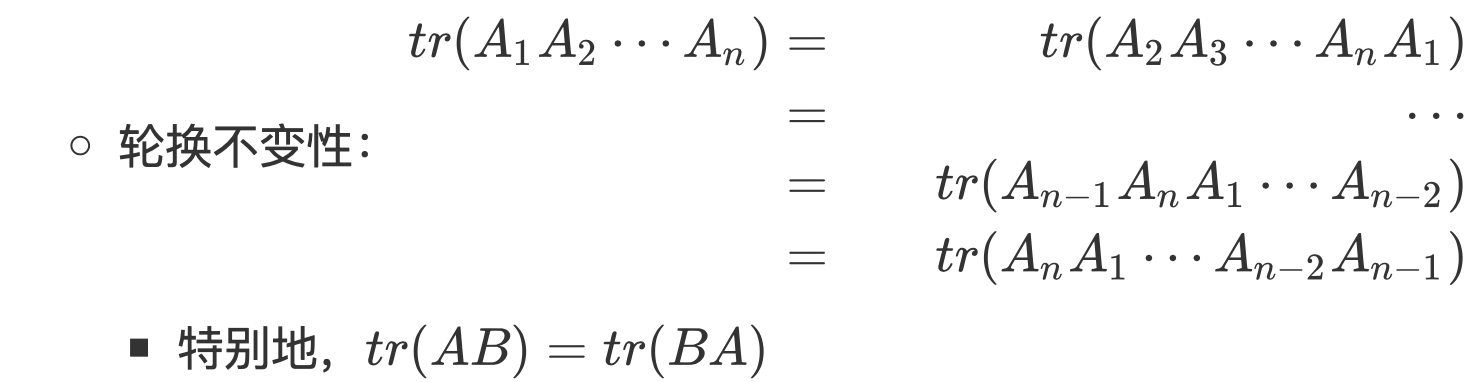
证明tr(AB)=tr(BA)：在以前的一篇博客中，我们证明了求矩阵乘积的迹与矩阵内积的等价性，即$<A, B>=tr(A^TB)$，利用此等式，我们有
$tr(AB)=<A^T, B>=<A, B^T>=<B^T, A>=tr(BA)$
2 -------------------------------------------------------------------------------------------------------------------------------
基本公式1：
记忆方法：若X右上角有转置，那求导结果就是矩阵A本身；若X右上角没有转置，那求导结果就是矩阵A的转置。
这里我们只证明第一个等式，即$\nabla tr(A^TX)=A$:
如果上式不够直观，展开将更直观：
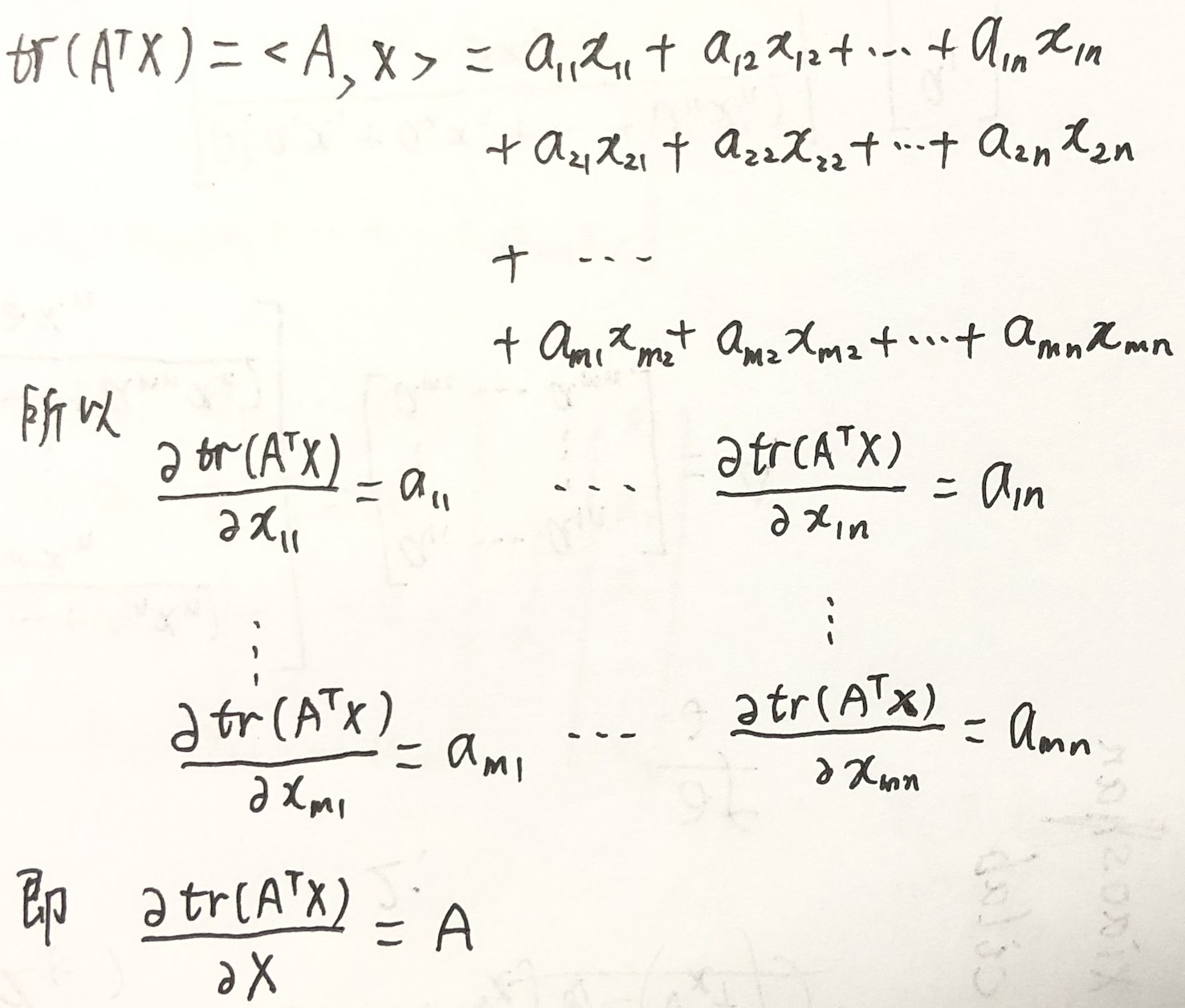
3 -------------------------------------------------------------------------------------------------------------------------------
基本公式2：
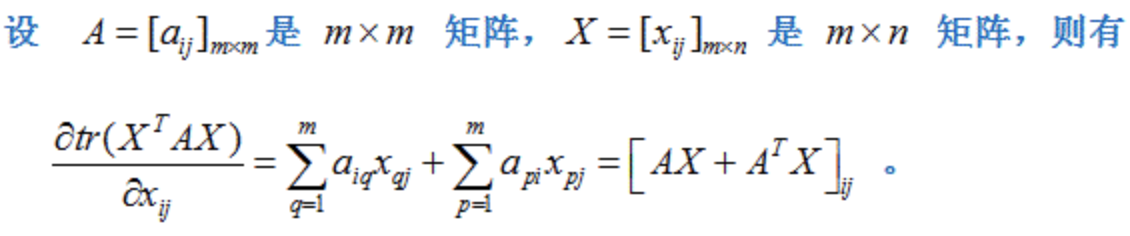
4 -------------------------------------------------------------------------------------------------------------------------------
核心公式：
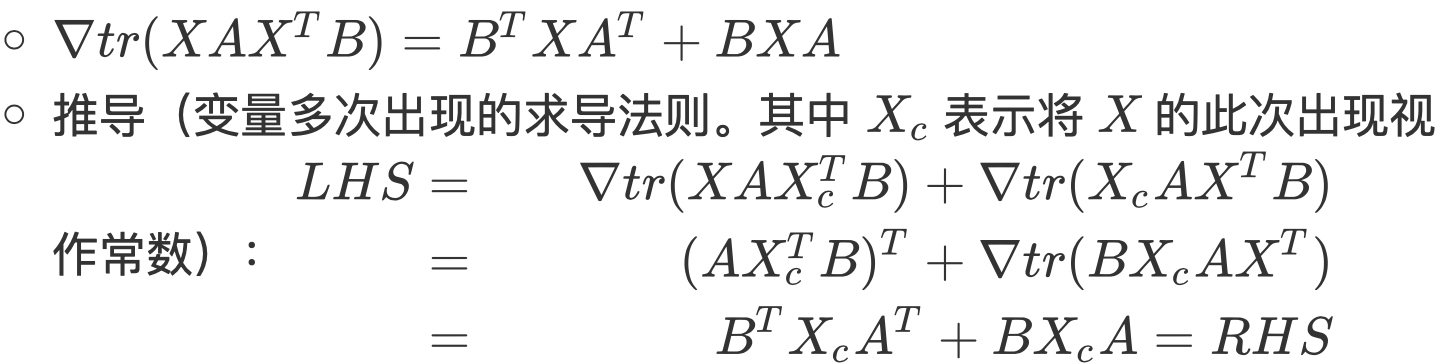
这里的证明推导用到了矩阵微分系列一末尾提到的求导法则
5 -------------------------------------------------------------------------------------------------------------------------------
其它公式：
