Python实现PCA降维

PCA算法

主成分分析（Principal Component Analysis，PCA）是最常用的一种降维方法，通常用于高维数据集的探索与可视化，还可以用作数据压缩和预处理等。PCA可以把具有相关性的高维变量合成为线性无关的低维变量，称为主成分。主成分能够尽可能保留原始数据的信息。PCA的计算涉及到对协方差矩阵的理解，这篇博客提供了协方差矩阵的相关内容。PCA的算法过程：

直接用numpy实现PCA

?

1 2 3 4 5 6 7 8 9 10 11

import numpy as np n = 2                                         # 取对应特征值最大的n个特征向量 data = np.random.rand(10, 5)                  # 生成10个样本，每个样本5个特征 mean = np.mean(data, axis=0)                  # 计算原始数据中每一列的均值，axis=0按列取均值 zeroCentred_data = data - mean                # 数据中心化，使每个feature的均值为0 covMat = np.cov(zeroCentred_data, rowvar=False)  # 计算协方差矩阵，rowvar=False表示数据的每一列代表一个feature featValue, featVec = np.linalg.eig(covMat)    # 计算协方差矩阵的特征值和特征向量 index = np.argsort(featValue)                 # 将特征值按从小到大排序，index是对应原featValue中的下标 n_index = index[-n:]                          # 取最大的n个特征值在原featValue中的下标 n_featVec = featVec[:, n_index]               # 取最大的两维特征值对应的特征向量组成映射矩阵 low_dim_data = np.dot(zeroCentred_data, n_featVec)     # 降维后的数据

下图可帮助理解：

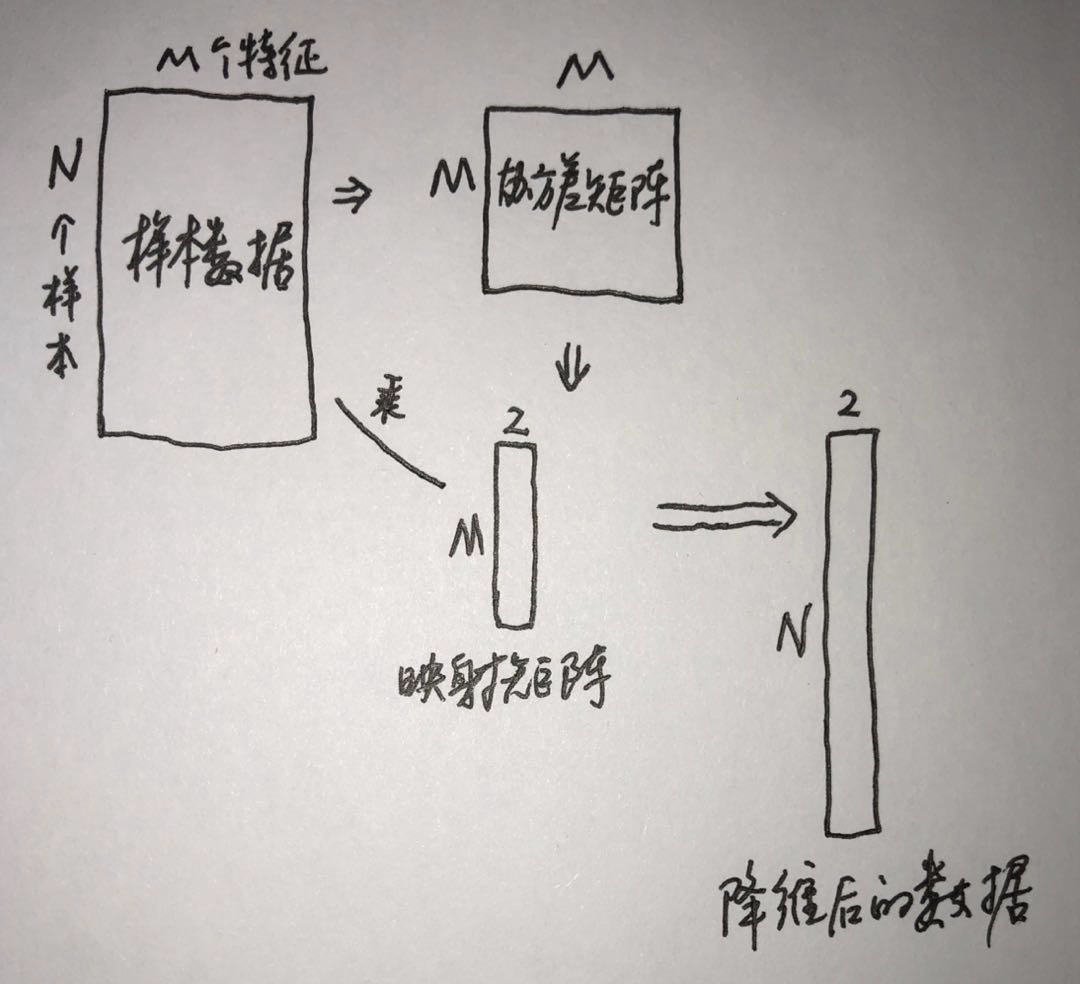
调用sklearn库实现PCA

这篇博客介绍了sklearn中PCA函数的具体参数。

?

1 2 3 4 5

import numpy as np from sklearn.decomposition import PCA data = np.random.rand(10, 5)            # 生成10个样本，每个样本5个特征 pca = PCA(n_components=2) low_dim_data = pca.fit_transform(data)  # 每个样本降为2维

 

参考资料

[1] Python机器学习应用

[2] python 矩阵分析（求方差，协方差矩阵，特征值，特征向量......）;PCA实现