逻辑回归(Logistic Regression)以及python实现
逻辑回归的原理是用逻辑函数把线性回归的结果(-∞,∞)映射到(0,1),因此本文先介绍线性回归和逻辑函数,然后介绍逻辑回归模型,再介绍如何优化逻辑函数的权重参数,最后用python实现一个简单的逻辑回归模型。
1. 线性回归
线性回归的数学表达式是:
其中是自变量,z是因变量,z的值域为(-∞,∞),是待求系数,不同的权重反映了自变量对因变量不同的贡献程度。这里我省略了,因为可以看做是,也就是的情况,所以实际上也包含到里面了。
2. 逻辑函数 (logistics函数, sigmoid函数)
Logistic的分布函数的数学表达式是 (逻辑回归- 知乎):
sigmoid函数是Logistic的分布函数在的特殊形式,也就是
(或者)
在这里我们不做区分,直接把sigmoid函数称为逻辑函数。
sigmoid函数图像:
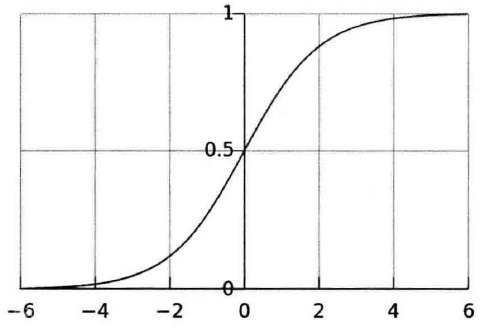
sigmoid函数有个很有用的特征,就是它的导数很容易用它的输出表示,即
这个结果也可以从下图中看出来,蓝色那条线代表,在x=0时导数最大,当x处于两头时,导数较小。
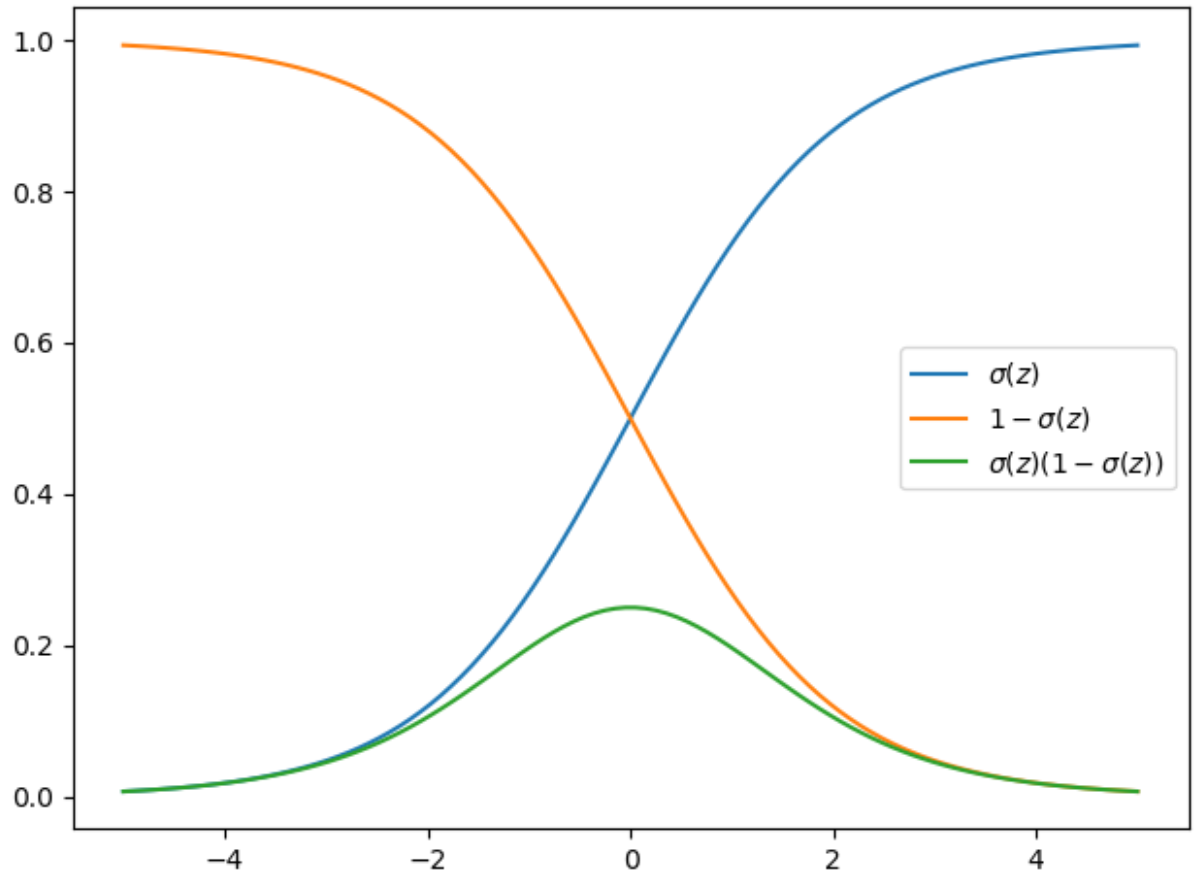
3. 逻辑回归模型
在逻辑回归模型中,对于二分类问题,该模型定义的条件概率是 (可以认为是该模型的一个假设):
这两个式子可以合并表示:
或者:
一个事件的几率()是指该事件发生的概率和该事件不发生的概率的比值。如果事件发生的概率是,那么该事件的几率是,该事件的对数几率( )或函数是。在逻辑回归二分类模型中,事件的对数几率是
上式表明,在逻辑回归中,对于二分类问题,输出的对数几率是输入的线性函数。
逻辑回归是线性分类器还是非线性分类器?判断一个模型是线性分类器还是非线性分类器,要根据这个模型的决策边界是否是线性的来判断。对于二分类问题,在决策边界上,模型的输出0类和1类的概率相等,也就是
因此,逻辑回归的决策边界是一个高维平面,因此逻辑回归是线性分类器。
4. 逻辑回归模型的参数优化
在逻辑回归模型中,对于给定的数据集,可以应用极大似然的思想得到模型训练目标,根据这个训练目标去优化模型参数。
优化目标是最大化所有训练样本出现的联合概率,即:
我们通常把argmax的问题转化为argmin的问题,即有:
记
的对数似然函数为:
对取极小值,即对各个参数求偏导:
应用式(1),有
有了梯度之后,我们就可以利用梯度下降法去一步步优化参数:
-----------------------------------------------------------------------------------
首先初始化;
for t = 1, 2, ......
-----------------------------------------------------------------------------------
逻辑回归一般用于二分类,对于多分类的情况,常常采用one-vs-all的策略。
【参考文献】
- 逻辑回归的常见面试点总结 (推荐)
- 哔哩哔哩:南开大学李文哲-机器学习基础课程 (视频讲解的很好,推荐)
- 逻辑回归(logistics regression)原理-让你彻底读懂逻辑回归
- 知乎【机器学习】逻辑回归
- 《机器学习算法原理与编程实践》郑捷,第五章第二节
- Neural Network and Deep Learning,Michael Nielsen,chapter 3
- 《机器学习》Mitshell,第四章
5.Python实现逻辑回归模型
训练数据:总共500个训练样本,链接https://pan.baidu.com/s/1qWugzIzdN9qZUnEw4kWcww,提取码:ncuj
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | import numpy as npimport matplotlib.pyplot as pltclass Logister(): def __init__(self, path): self.path = path def file2matrix(self, delimiter): fp = open(self.path, 'r') content = fp.read() # content现在是一行字符串,该字符串包含文件所有内容 fp.close() rowlist = content.splitlines() # 按行转换为一维表 # 逐行遍历 # 结果按分隔符分割为行向量 recordlist = [list(map(float, row.split(delimiter))) for row in rowlist if row.strip()] return np.mat(recordlist) def drawScatterbyLabel(self, dataSet): m, n = dataSet.shape target = np.array(dataSet[:, -1]) target = target.squeeze() # 把二维数据变为一维数据 for i in range(m): if target[i] == 0: plt.scatter(dataSet[i, 0], dataSet[i, 1], c='blue', marker='o') if target[i] == 1: plt.scatter(dataSet[i, 0], dataSet[i, 1], c='red', marker='o') def buildMat(self, dataSet): m, n = dataSet.shape dataMat = np.zeros((m, n)) dataMat[:, 0] = 1 dataMat[:, 1:] = dataSet[:, :-1] return dataMat def logistic(self, wTx): return 1.0/(1.0 + np.exp(-wTx)) def classfier(self, testData, weights): prob = self.logistic(sum(testData*weights)) # 求取概率--判别算法 if prob > 0.5: return 1 else: return 0if __name__ == '__main__': logis = Logister('testSet.txt') print('1. 导入数据') inputData = logis.file2matrix('\t') target = inputData[:, -1] m, n = inputData.shape print('size of input data: {} * {}'.format(m, n)) print('2. 按分类绘制散点图') logis.drawScatterbyLabel(inputData) print('3. 构建系数矩阵') dataMat = logis.buildMat(inputData) alpha = 0.1 # learning rate steps = 600 # total iterations weights = np.ones((n, 1)) # initialize weights weightlist = [] print('4. 训练模型') for k in range(steps): output = logis.logistic(dataMat * np.mat(weights)) errors = target - output print('iteration: {} error_norm: {}'.format(k, np.linalg.norm(errors))) weights = weights + alpha*dataMat.T*errors # 梯度下降 weightlist.append(weights) print('5. 画出训练过程') X = np.linspace(-5, 15, 301) weights = np.array(weights) length = len(weightlist) for idx in range(length): if idx % 100 == 0: weight = np.array(weightlist[idx]) Y = -(weight[0] + X * weight[1]) / weight[2] plt.plot(X, Y) plt.annotate('hplane:' + str(idx), xy=(X[0], Y[0])) plt.show() print('6. 应用模型到测试数据中') testdata = np.mat([-0.147324, 2.874846]) # 测试数据 m, n = testdata.shape testmat = np.zeros((m, n+1)) testmat[:, 0] = 1 testmat[:, 1:] = testdata print(logis.classfier(testmat, np.mat(weights))) # weights为前面训练得出的 |
训练600个iterations,每100个iterations输出一次训练结果,如下图:
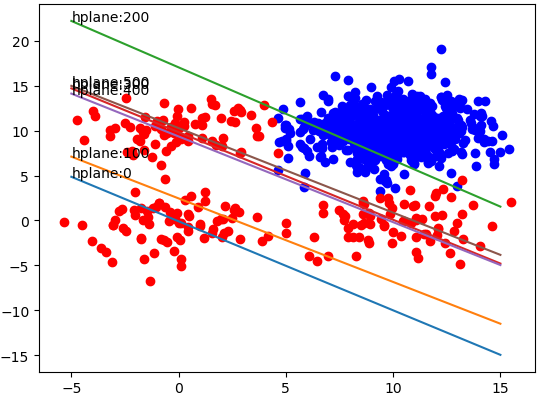





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通