软件基础个人工程——数独3
GITHUB项目地址:
https://github.com/hhz-hhz/Sudoku_software_engineer.git
软工基础个人项目——数独1
软工基础个人项目——数独2
二、设计阶段
5、对于设计文档的补充
除了对于代码的设计外之前还需要对单元测试进行设计:
DefiningBeginning.cpp中:
1)int ChageStringToNumber(char s[])进行单元测试:测试输入字符串是数字的情况和输入字符串不是数字的情况
2)void WritePutsToFile(FILE* fp, SUDOKU m)进行单元测试:测试是否能够对文件进行写入
SolvingSudoku.cpp中:
1)inline bool CheckingForDFS(int n, int key)进行单元测试:需要进行符合数独规范和不符合数独规范的验证
2)inline int SolvingByDFS(int n)进行单元测试:对于一个带求解的数独进行测试
3)bool SolvingSudoku(FILE* rfp)进行单元测试:对于一个固定文件中的数独进行求解
GeneratingSudoku.cpp中:
1)inline void MovingStep()进行单元测试:查看是否能够运行出符合要求的位移矩阵
main.cpp中:
1)int main(int argc, char* argv[])进行单元测试:正确的命令和错误的命令、是否能够正确的求解数独,是否能够生成数独
三、编程阶段
1、代码说明
1)、DefiningBeginning.cpp
1 | int ChageStringToNumber(char s[])\\利用isdigit()判断是否是数字字符 |
1 | void WritePutsToFile(FILE* fp, SUDOKU m)\\由于生成数独和求解数独都需要写入文件,所以将它变成函数 |
2)、SolvingSudoku.cpp
检查数独:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | inline bool CheckingForDFS(int n, int key)\\判断key是否能够填入{ for (int i = 0; i < 9; i++)\\判断n所在横列是否合格 { int j = n / 9; if (DoSudoku.map[j][i] == key)return false; } for (int i = 0; i < 9; i++)\\判断n所在竖列是否合格 { int j = n % 9; if (DoSudoku.map[i][j] == key)return false; } int x = n / 9 / 3 * 3; int y = n % 9 / 3 * 3; for (int i = x; i < x + 3; i++)\\判断n所在的9宫格是否合格 { for (int j = y; j < y + 3; j++) { if (DoSudoku.map[i][j] == key)return false; } } return true;} |
DFS求解数独:
1 | inline int SolvingByDFS(int n) |
求解文件中的多个数独:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | bool SolvingSudoku(FILE* rfp){ FILE *wfp; errno_t err; err = fopen_s(&wfp, "sudoku.txt", "w"); if (err != 0) { return false; } char blank; do { for (int i = 0; i < 9; i++)\\读入文件 { for (int j = 0; j < 9; j++) { fscanf_s(rfp, "%d%c", &DoSudoku.map[i][j], &blank, sizeof(int) + sizeof(char)); } } SolvingByDFS(0); sign = false;\\递归停止标志 WritePutsToFile(wfp, DoSudoku);\\写入文件中 } while (fscanf_s(rfp, "%c", &blank, sizeof(char)) != EOF); if (wfp != 0)fclose(wfp); return true;} |
3)GeneratingSudoku.cpp
生成平移步数矩阵:MovingStepDic[72][9]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | inline void MovingStep(){<br> \\平移方式的种类 int MovingDic1[2][3] = { { 0,3,6 },{ 0,6,3 } }; int MovingDic2[6][3] = { { 1,4,7 },{ 1,7,4 },{ 4,1,7 },{ 4,7,1 },{ 7,4,1 },{ 7,1,4 } }; int MovingDic3[6][3] = { { 2,5,8 },{ 2,8,5 },{ 5,2,8 },{ 5,8,2 },{ 8,2,5 },{ 8,5,2 } }; int step[10]; int count = 0;<br> \\求取2*6*6种变换方式矩阵 for (int i = 0; i < 6; i++) { for (int j = 0; j < 6; j++) { for (int k = 0; k < 2; k++) { memcpy_s(&step[0], 3 * sizeof(int), &MovingDic1[k][0], 3 * sizeof(int)); memcpy_s(&step[3], 3 * sizeof(int), &MovingDic2[j][0], 3 * sizeof(int)); memcpy_s(&step[6], 3 * sizeof(int), &MovingDic3[i][0], 3 * sizeof(int)); memcpy_s(&MovingStepDic[count], 9 * sizeof(int), &step[0], 9 * sizeof(int)); count++; } } }} |
生成数独:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | bool GeneratingSudoku(int n){ FILE *fp; errno_t err; err = fopen_s(&fp, "sudoku.txt", "w"); if (err != 0) { return false; } MovingStep(); int RequestFirstline[9] = { 8,9,1,2,3,4,5,6,7 };\\按照规定,第一位是8 int JointLine[18]; int num = 0; SUDOKU ResultingSudoku; memset(ResultingSudoku.map, 0, sizeof(ResultingSudoku.map)); while (next_permutation(&RequestFirstline[1], &RequestFirstline[9]))\\生成全排列 { if (num >= n)break; for (int i = 0; i < 72; i++) { if (num >= n)break;<br> //生成例如891234567891234567的18位数组方便计算 memcpy(JointLine, RequestFirstline, sizeof(RequestFirstline)); memcpy(&JointLine[9], RequestFirstline, sizeof(RequestFirstline));<br> //对JointLine数组进行截取 int j = num % 72; for (int k = 0; k < 9; k++) { int l = MovingStepDic[j][k]; memcpy(&ResultingSudoku.map[k], &JointLine[l], 9 * sizeof(int)); }<br> //写入文件 WritePutsToFile(fp, ResultingSudoku); num++; } } if(fp!=0)fclose(fp); return true;} |
2、代码质量分析
3、代码性能分析
1)、对于生成数独进行性能分析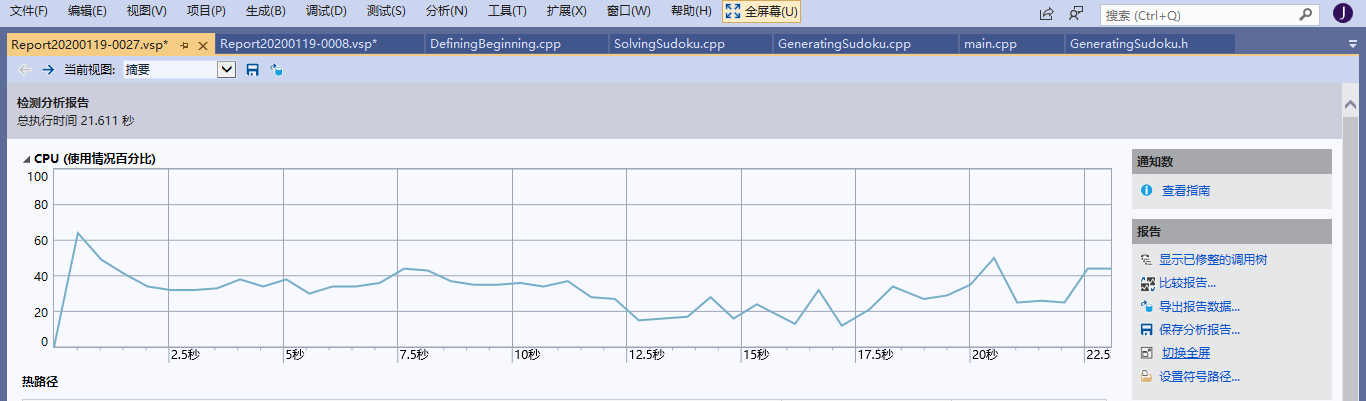
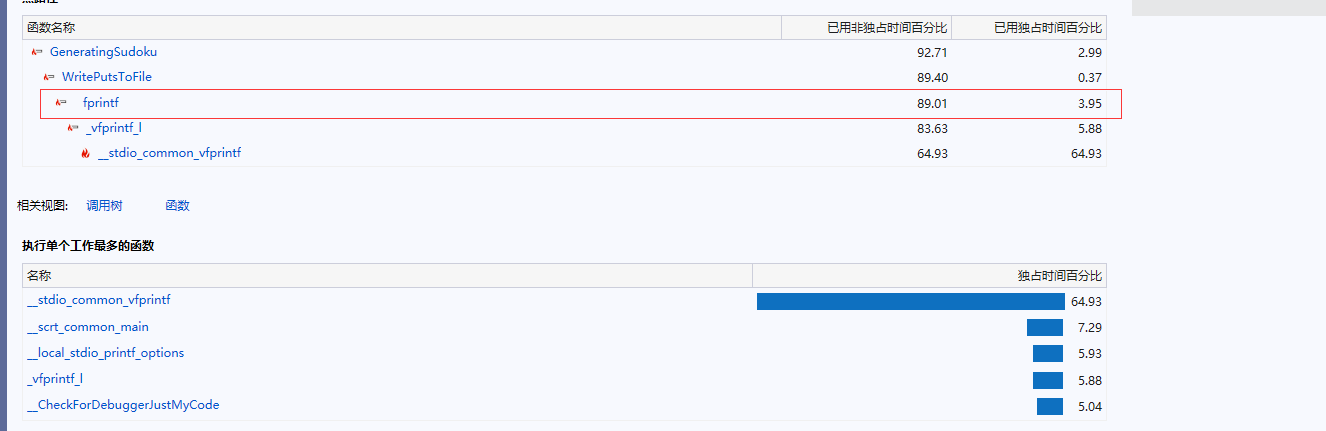
可以看到fprintf和WritePutsToFile()占用较大的比重,因为WritePutsToFile()中也较多使用fprintf,所以对写入文件函数WritePutsToFile进行优化比较合适。
原写入为:

本来设计说这样的代码虽然有些粗鲁,但是比较快。因为会一次性写入9个数字及空格。如果要做优化,不如一次性写入所有元素。
优化后写入:

再对其进行性能分析:

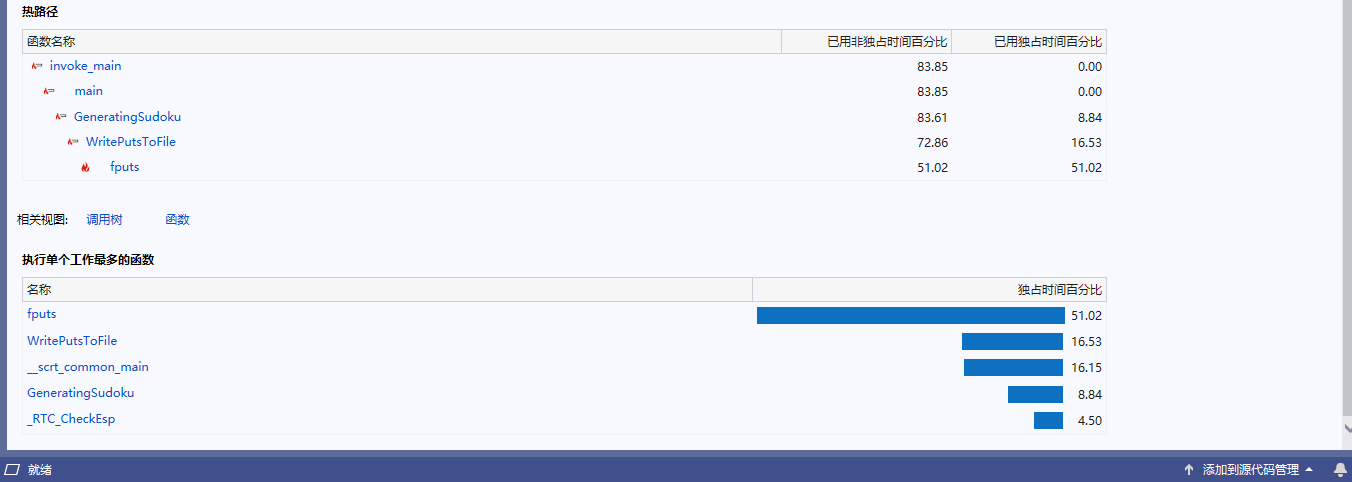
经过优化后,时间上有了较大的改进。
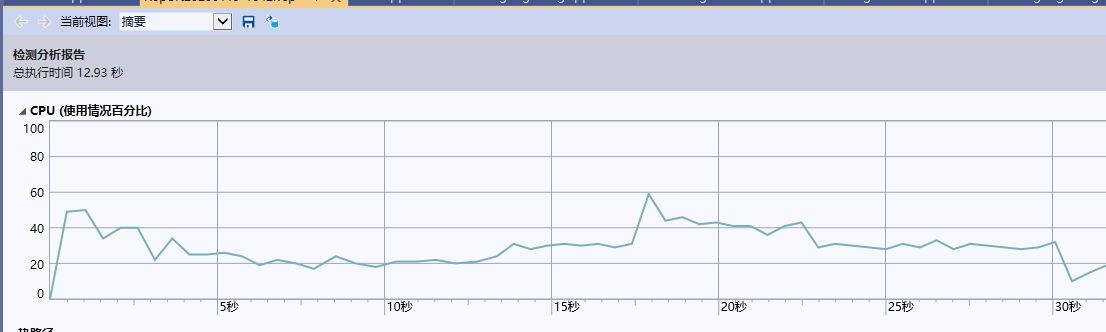
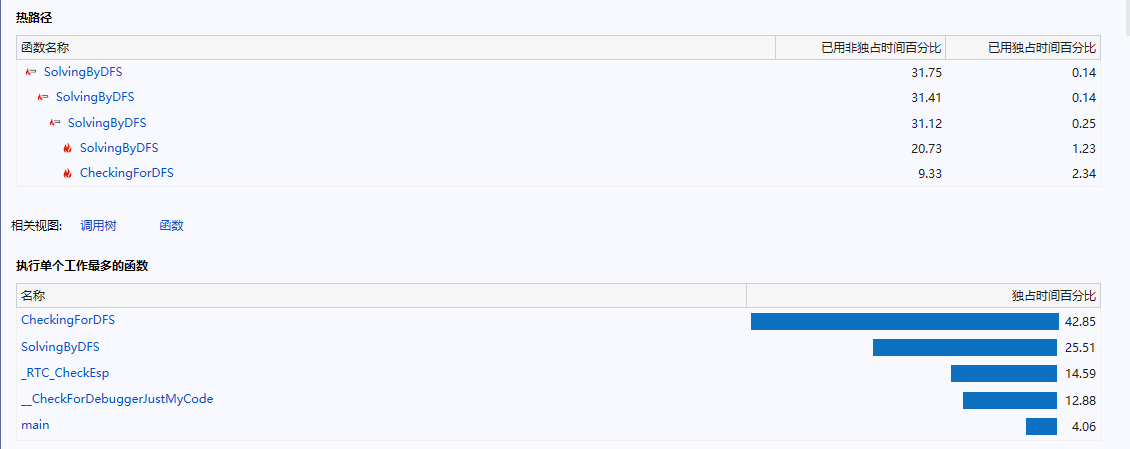
2)、对于求解数独进行性能分析


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步