算法基础(1)必知必会

　　好久没更新博客了，拖更严重。夜晚打开电脑补上

　　　　

算法的时间复杂度:

时间频度:

时间频度:一个算法花费的时间和算法中语句的执行次数成正比,哪个算法中语句的执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

 

时间频度中可以忽略的点:

1.忽略常数项

example:

T(n)=2n+20
T(n)=2n
2n+20可以省略常数20。

 

 

2.忽略低次项

example:

T(n)=2n^2+3n+10
T(n)=n^2+5n+5
其中可以忽略低次项和常数项
那么最后结果就是:
T(n)=2n^2
T(n)=n^2

 

 

 

3.忽略系数:

exmaple:

T(n)=3n^2+3n+10
T(n)=5n^2+5n+5

在数量级很大的情况下，可以忽略系数，低次项和常数项:

最后结果是:

T(n)=n^2
T(n)=n^2
如果是
T(n)=n^3+3n
T(n)=5n^3+5n

 

他的曲线不会重合，只会渐行渐远，说明立方系数结果远远超过平方系数数.立方属于高次项，不属于低次项。

随着n的变大，可以忽略常数项，低次项和系数

算法时间复杂度:

T(n)=O
用O表示时间复杂度
example:
T(n)=3n^2+3n+10
T(n)=5n^2+5n+5
最后结果是:
T(n)=n^2
T(n)=n^2
两者时间复杂度相同均为O(n^2)

 

常见的时间复杂度:

(1)常数阶O(1)

(2)对数阶O(log2^n)

(3)线性阶O(n)

(4)线性对数阶O(nlog2^n)

(5)平方阶O(n^2)

(6)立方阶O(n^3)

(7)k次方阶O(n^k)

(8)指数阶O(2^n)

复杂度由小到大排序:(1)<(2)<(3)<(4)<(5)<(6)<(7)<(8)

复杂度越高,程序执行效率越低

(1)常数阶O(n):

无论代码执行多少次,只要没有循环等复杂逻辑,那么这个代码的时间复杂度就是O(1)

 

 

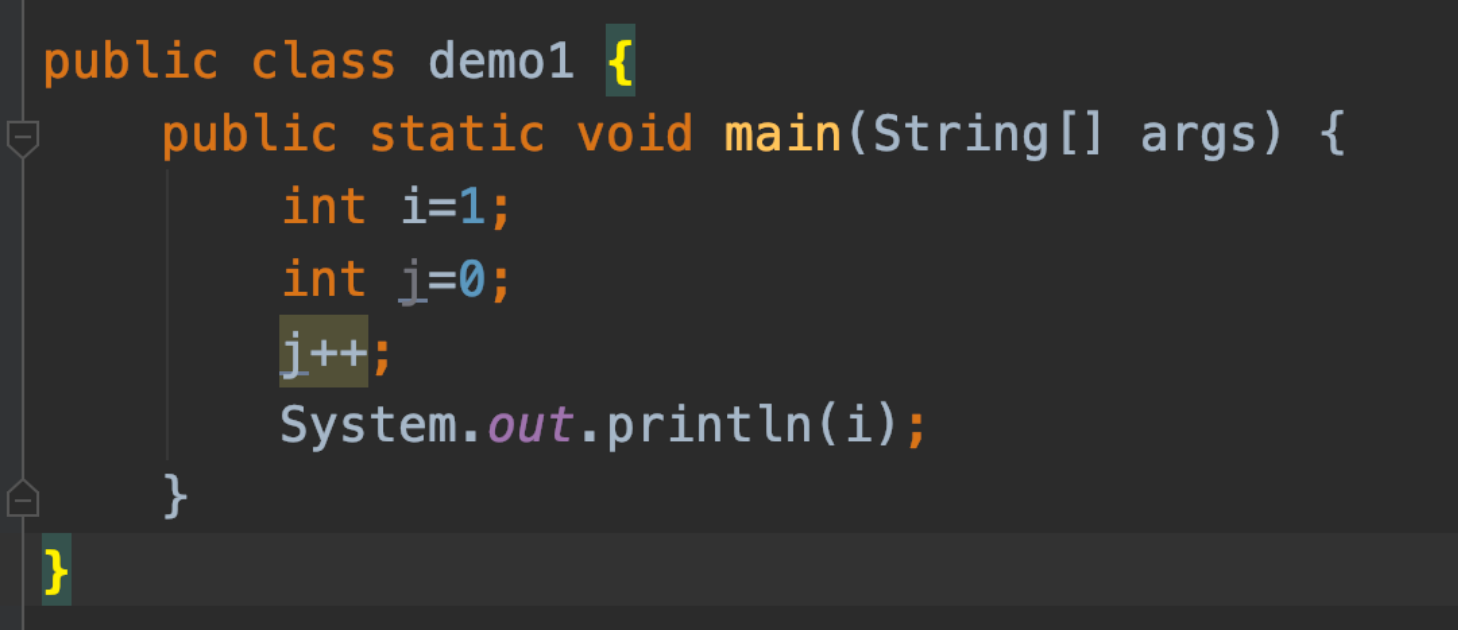
(2)对数阶O(log2^n):

使用一次while循环

 

 

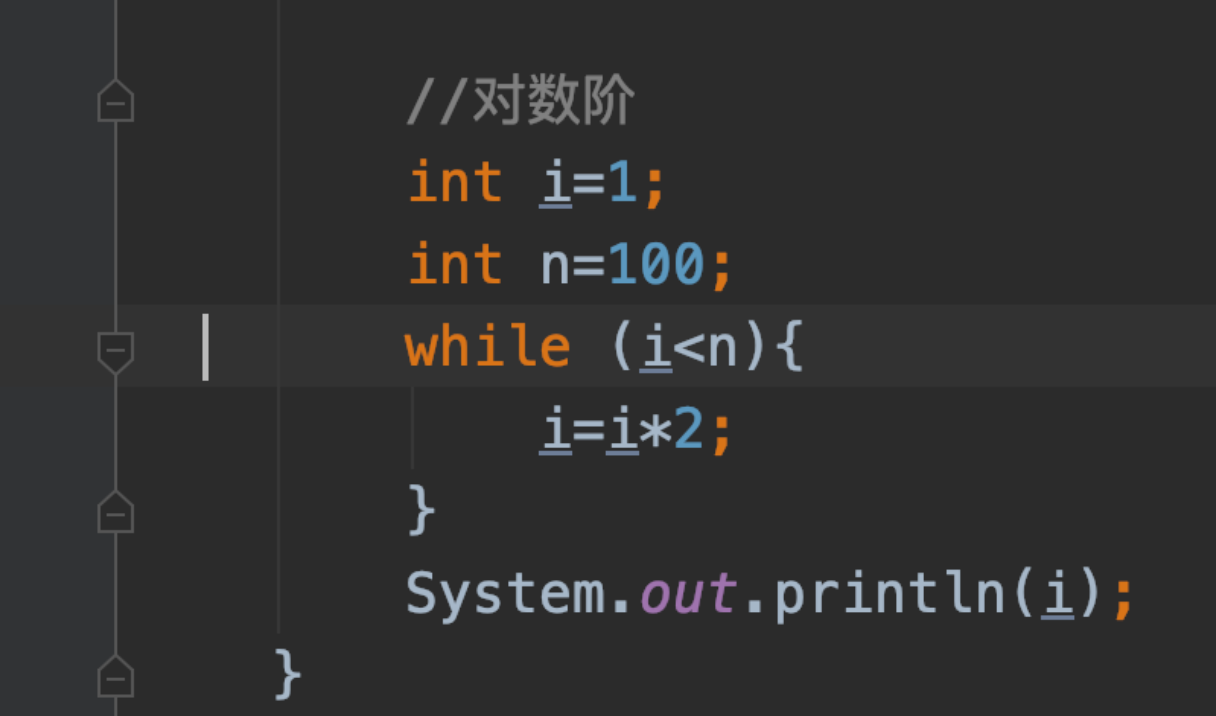
稍微修改代码:

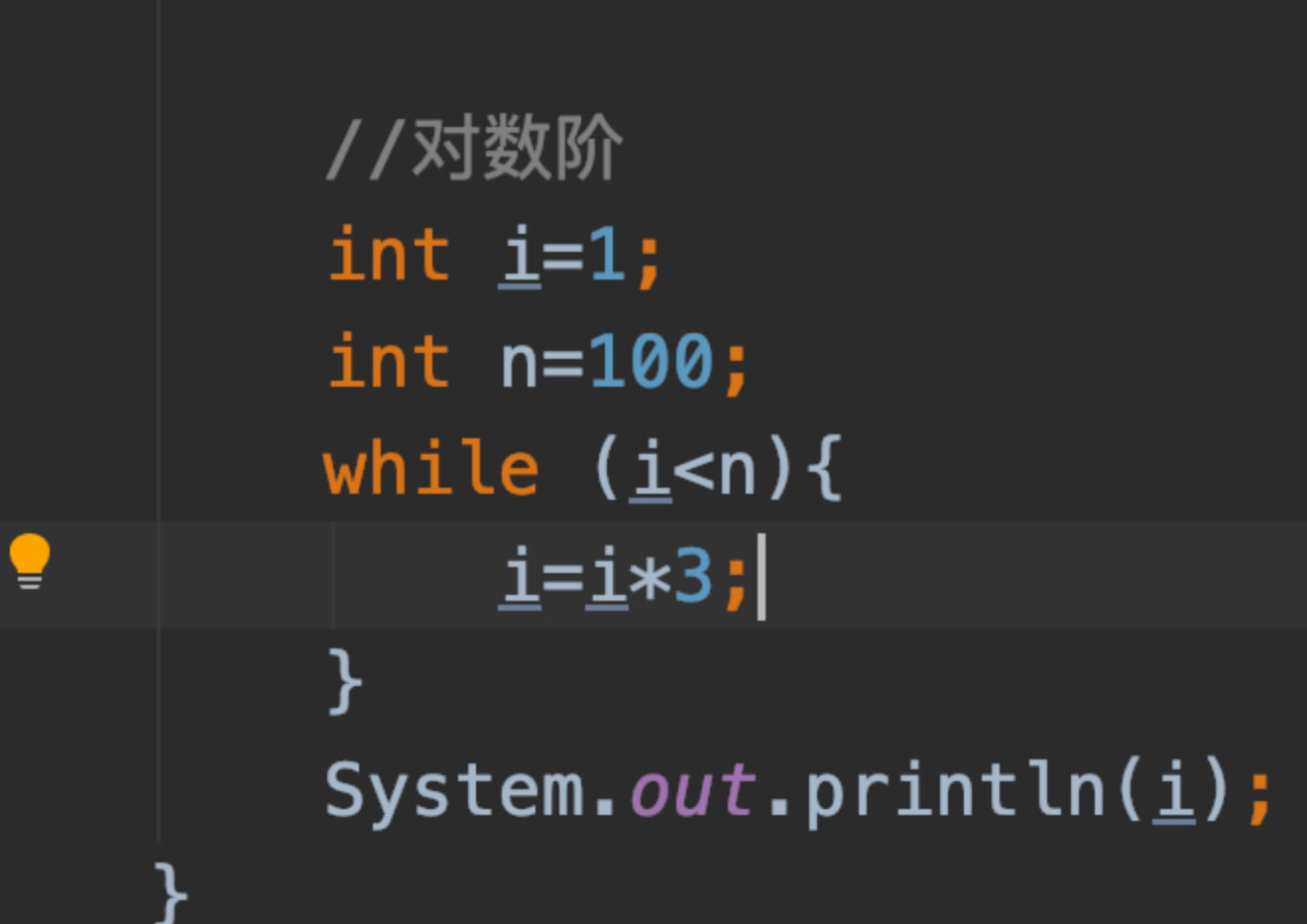
此时对数阶为:log3^n

 

(3)线性阶O(n):

单层for循环就是线性阶

 

 

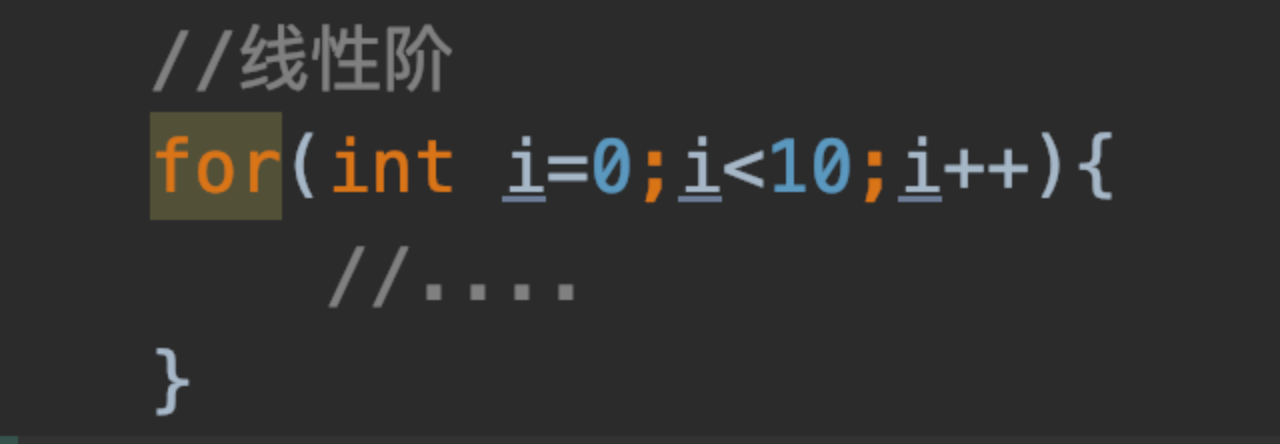
(4)线性对数阶O(nlog2^n):

 

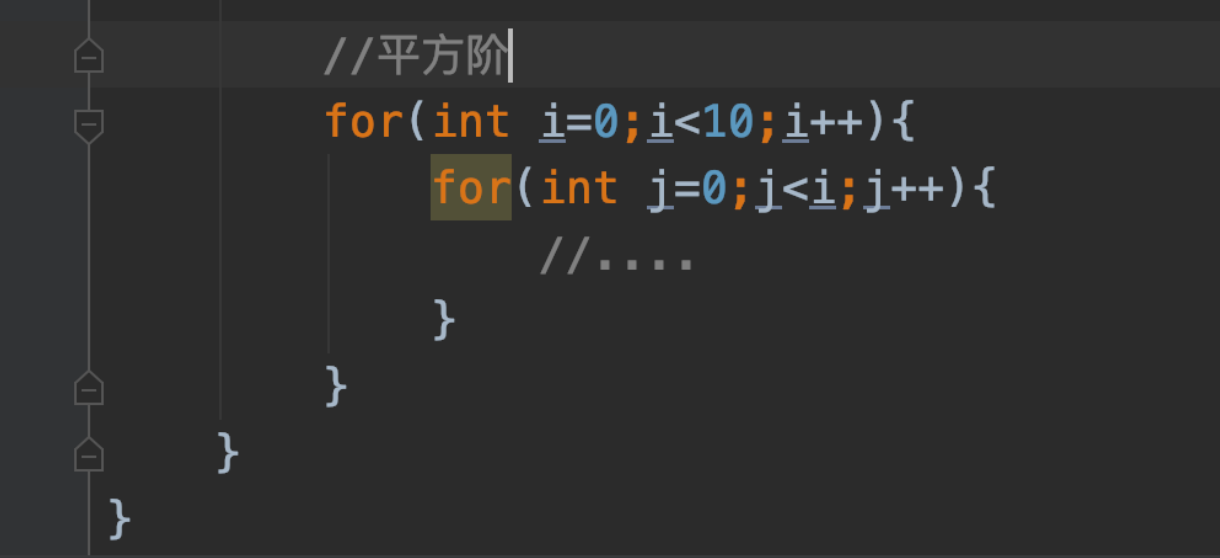
(5)平方阶O(n^2):

二次for循环就是平方阶

 

 

 

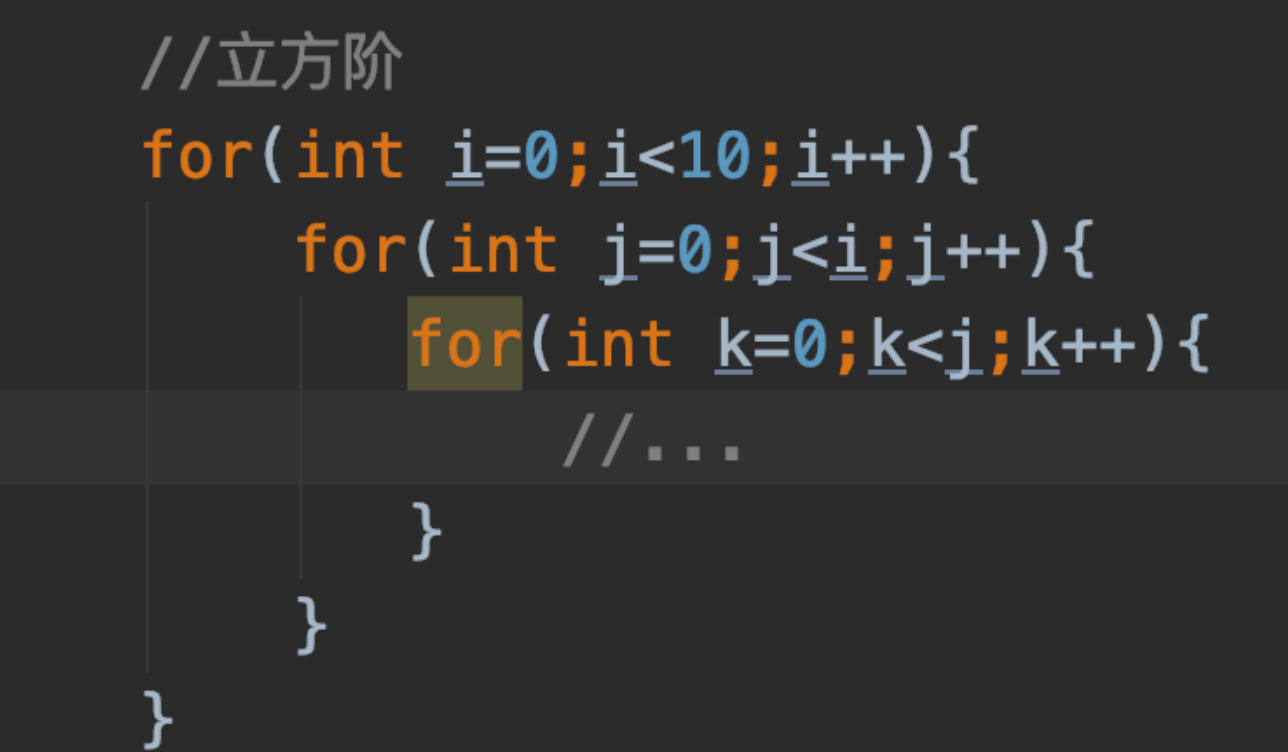
6)立方阶O(n^3):

三次for循环就是立方阶

 

 

 

(7)k次方阶O(n^k):

假设k=3,那么就是n^3就是for循环三次

 

 

 

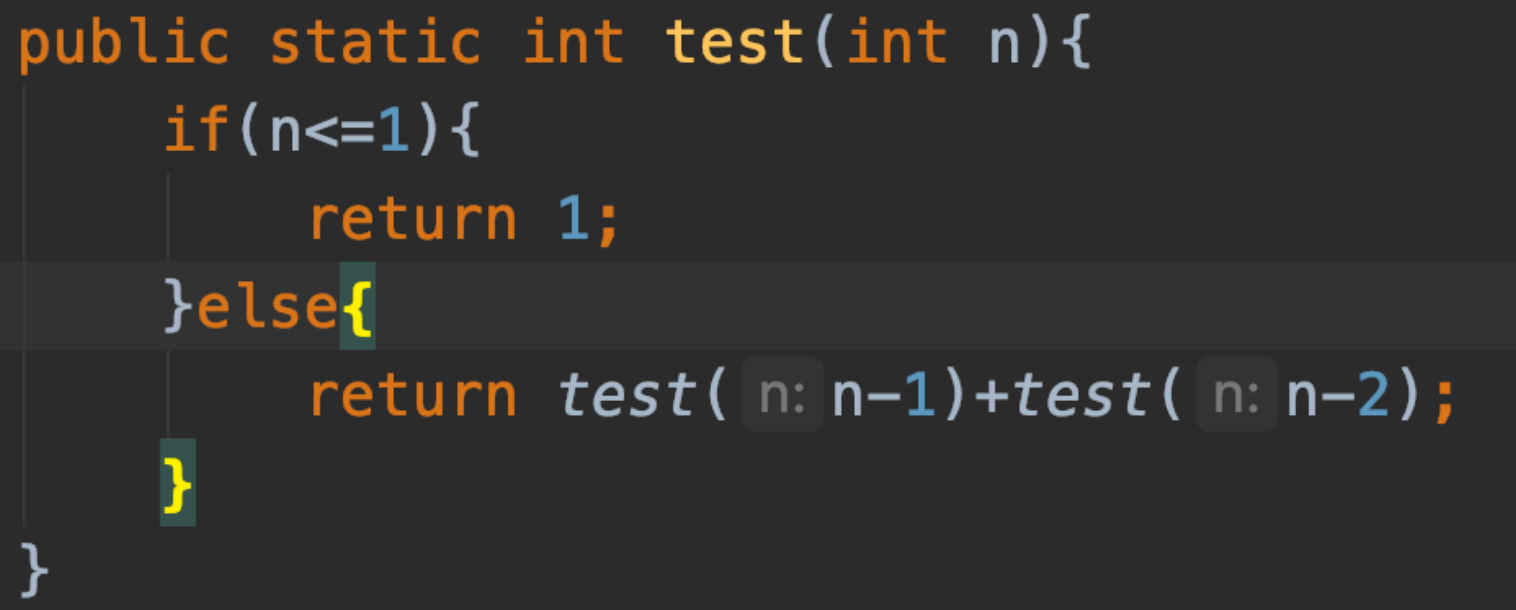
(8)指数阶O(2^n):

递归就是典型的指数阶复杂度,所以写代码尽量避免使用递归

 

 

使用算法涉及到用考虑到时间复杂度。

还有一种就是使用空间换时间:

从用户体验来看，更注重程序执行的速度,一些缓存产品如redis,就是典型的用空间换取时间,用于提升程序的执行速度。

 

参考:韩顺平java数据结构和算法