问题描述
给定n个不同的正整数(数组num),整数k(k < = n)以及一个目标数字target。在这n个数里面找出k个数,使得这k个数的和等于目标数字,求问有多少种方案?
解决思路
该类问题可以使用动态规划求解。
令dp[i][j][z]表示在数组num的【前i个元素中取j个数和为z】的组合的个数,则可得到以下递推式:
dp[i][j][z] = dp[i-1][j][z] + dp[i-1][j-1][z-num[i]]
该递推式的意义是:对于数组中第i个元素,存在两种可能性,1)选取的j个数中包含它;2)选取的j个数中不包含它。对于1),可能的组合情况数目为 dp[i-1][j-1][z-num[i]];对于2)可能的组合情况的数目为 dp[i-1][j][z] ,二者加起来,即为所有可能的组合的数量。
另外还注意到,i只与i-1有关,所以我们可以把三维数组降维成二维数组(类似于背包问题中的降维):
dp[j][z] = dp[j][z] + dp[j-1][z-num[i]]
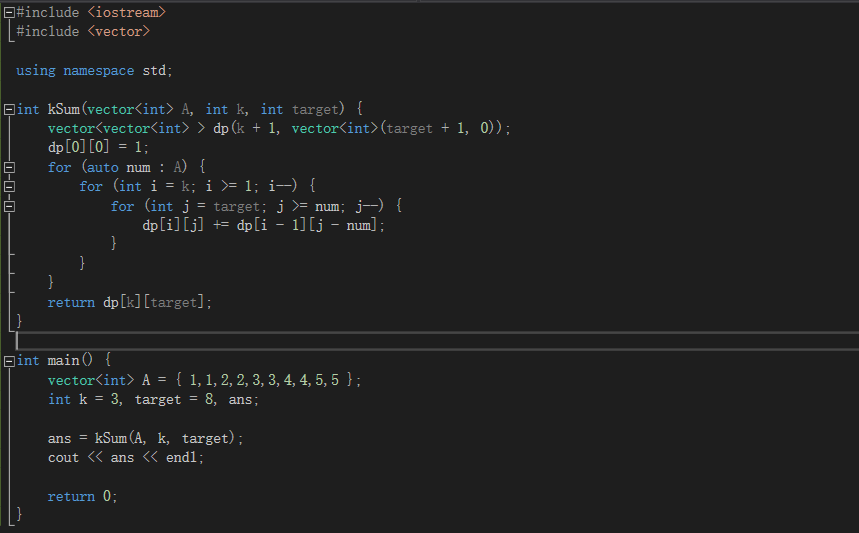
编程练习链接:https://leetcode-cn.com/problems/3sum-with-multiplicity/description/



