炮兵阵地

来源 : https://www.acwing.com/problem/content/294/

题意

司令部的将军们打算在 N*M 的网格地图上部署他们的炮兵部队。一个 N*M 的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

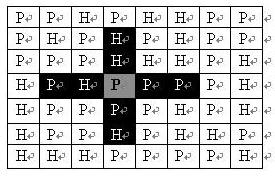
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符(‘P’或者’H’)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

数据范围

N≤100,M≤10

#include <bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
inline int lowbit(int x) { return x & (-x); }
#define ll long long
#define pb push_back
#define PII pair<int, int>
#define fi first
#define se second
#define inf 0x3f3f3f3f
const int N = 110, M = 1 << 11;
int n, m;
int g[N], cnt[M];
vector<int> state;
ll f[2][M][M];

bool check(int x) {
    for (int i = 0; i < m; ++i)
        if ((x >> i & 1) && (x >> i + 1 & 1)) return false;
    for (int i = 0; i < m; ++i)
        if ((x >> i & 1) && (x >> i + 2 & 1)) return false;
    return true;
}
    
        
int count(int x) {
    int res = 0;
    for (int i = 0; i < m; ++i) res += x >> i & 1;
    return res;
}    
    
int main() {
    IO;
    cin >> n >> m;
    for (int i = 0; i < n; ++i) 
        for (int j = 0; j < m; ++j) {
            char p;
            cin >> p;
            g[i] += (p == 'H') << j;
        }
    
    for (int i = 0; i < 1 << m; ++i) 
        if (check(i)) {
            state.pb(i);
            cnt[i] = count(i);
        }
        

    for (int i = 0; i < n + 2; ++i)
        for (int j = 0; j < state.size(); ++j)
            for (int k = 0; k < state.size(); ++k)
                for (int u = 0; u < state.size(); ++u) {
                    int a = state[u], b = state[j], c = state[k];
                    if ((a & b) || (a & c) || (b & c)) continue;
                    if (c & g[i]) continue;
                    f[i & 1][j][k] = max(f[i & 1][j][k], f[i - 1 & 1][u][j] + cnt[c]);
                }
                   
    cout << f[n + 1 & 1][0][0] << endl;  
    return 0;
}