Mandelbrot set 以parallel_for_实现

 parallel_for_ 的参数说明

void cv::parallel_for_ (const Range &range, const ParallelLoopBody &body, double nstripes=-1.)

static void cv::parallel_for_ (const Range &range, std::function< void(const Range &)> functor, double nstripes=-1.)

const Range &range：是你准备要处理的像素范围

const ParallelLoopBody &body：body是你自己定义的类的对象，该类要求从ParallelLoopBody继承

std::function< void(const Range &)> functor：fuction是函数指针模板类，< void(const Range &)>是函数指针所指向的函数，void表示该函数返回为空，(const Range &)是函数形参类型。

                                                                        其实我一直有个疑问，第一个参数range与< void(const Range &)>是怎么关联起来的。

double nstripes：暂时还不知道啥意思：），有知道的请指点个一二，谢了先：）。

在本例中调用了第2个重载函数static void cv::parallel_for_ (const Range &range, std::function< void(const Range &)> functor, double nstripes=-1.)，

采用函数形式对Range范围的像素进行处理，相对第1个自定义类的方式更简洁一些。

 我们将以绘制曼德布罗集合为例，展示如何从常规的顺序代码轻松地修改代码以实现并行化计算。

曼德布罗特集理论：

曼德布罗特集的定义是以数学家本诺·曼德布罗特的名字命名的，由阿德里安·杜瓦迪命名。它因其在数学领域之外的形象表示而闻名，因为它是一个类分形的例子，一个在每个尺度上重复显示模式的数学集合（更进一步说，曼德布罗特集是自相似的，因为整个形状可以在不同的尺度上反复看到）。对于更深入的介绍，您可以查看相应的维基百科文章。在这里，我们将只介绍绘制曼德布罗特集的公式（来自上述维基百科文章）。

Mandelbrot集合是复平面上 的值集，对于这些值，在二次映射的迭代下，从0开始的轨道保持收敛。  二次迭代映射表达式如下：

                                         

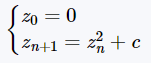
 这就是说，复数c是Mandelbrot集合的一部分，如果从z0=0开始并反复应用迭代，无论n有多大，zn的绝对值仍然保持有界。这也可以表示为                                     

                                       

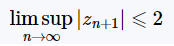
 伪代码

🔍发现奇迹，每一像素藏着无限秘密！在五彩光阑的图像宇宙里，我们一起用最简单的逃逸时间算法，探索复数世界的无尽边界。🌈Mandelbrot集的每一点色彩，都是递归关系的精彩演绎。我们一起来看看你的世界里，哪些像素会逃逸，哪些会在迭代中沉淀。🌟 加入我们的旅程，让数字艺术绽放在你的屏幕上。🎨 不断迭代，细节渐显，时间仿佛也在这一花一世界中流转。🎯 专注每个细节，渲染出属于你的Mandelbrot世界地图。🚀 跟着我，一起绘制未知，记录每一次迭代的成长轨迹。🎓

For each pixel (Px, Py) on the screen, do:
{
    x0 = scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2, 1));
    y0 = scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1));
    x = 0.0;
    y = 0.0
    iteration = 0
    max_iteration = 1000
    while (x*x + y*y < 2*2 AND iteration < max_iteration) {
        xtemp = x*x - y*y + x0
        y = 2*x*y + y0
        x = xtemp
        iteration = iteration + 1
    }
    color = palette[iteration]
    plot(Px, Py, color)
}

为了把理论与伪代码联系起来，我们将曼德布罗特表达式写入如下表达式：

 

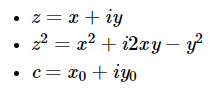
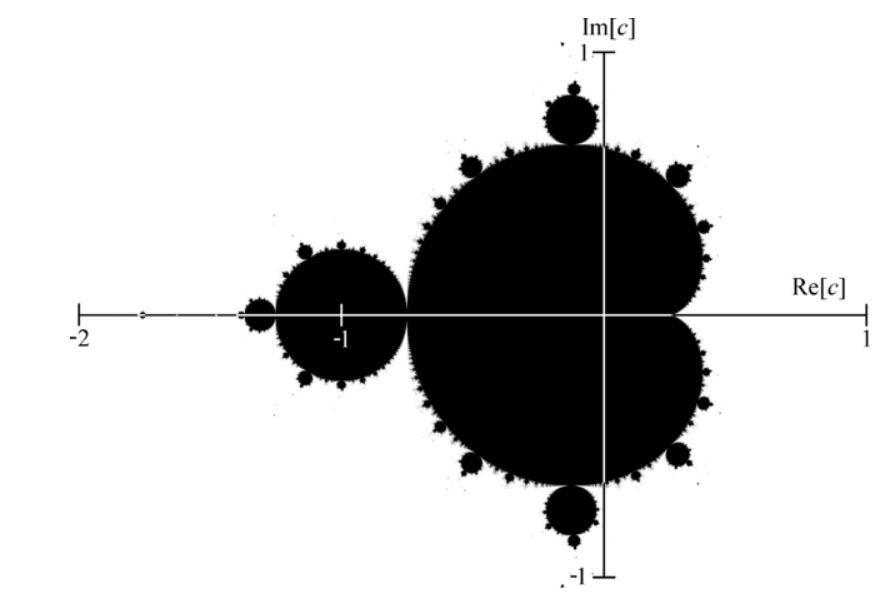
 在这个图中，我们回忆一下实数部分位于x轴上，虚数部分位于y轴上。您可以看到，如果我们放大特定位置，整个形状可以重复出现。

使用线性尺度变换不足以感知灰度变化。为了克服这一点，我们将通过使用平方根尺度变换来增强感性任知：

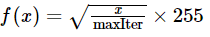
（借鉴自Jeremy D. Frens在他的博客文章中的方法：Programming During Recess - Color Schemes for Mandelbrot Sets (programming-during-recess.net)）

 

 

 

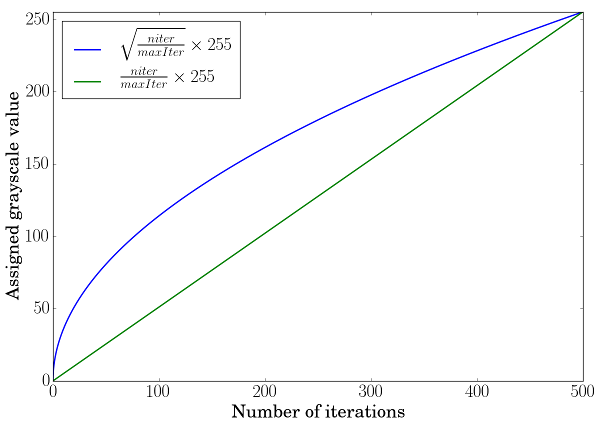
实现代码如下：

//1.Escape time algorithm implementation

int mandelbrot(const complex<float> &z0, const int max)
{
    complex<float> z = z0;
    for (int t = 0; t < max; t++)
    {
        if (z.real()*z.real() + z.imag()*z.imag() > 4.0f) return t;
        z = z*z + z0;
    }
    return max;
}
//2.Sequential Mandelbrot implementation

int mandelbrotFormula(const complex<float> &z0, const int maxIter=500)
{
    int value = mandelbrot(z0, maxIter);
    if(maxIter - value == 0)
    {
        return 0;
    }

    return cvRound(sqrt(value / (float) maxIter) * 255);
}
//3.Parallel Mandelbrot implementation

class ParallelMandelbrot : public ParallelLoopBody
{
public:
    ParallelMandelbrot (Mat &img, const float x1, const float y1, const float scaleX, const float scaleY)
        : m_img(img), m_x1(x1), m_y1(y1), m_scaleX(scaleX), m_scaleY(scaleY)
    {  }
    virtual void operator ()(const Range& range) const CV_OVERRIDE
    {
        for (int r = range.start; r < range.end; r++)
        {
            int i = r / m_img.cols;
            int j = r % m_img.cols;

            float x0 = j / m_scaleX + m_x1;
            float y0 = i / m_scaleY + m_y1;

            complex<float> z0(x0, y0);
            uchar value = (uchar) mandelbrotFormula(z0);
            m_img.ptr<uchar>(i)[j] = value;
        }
    }

    ParallelMandelbrot& operator=(const ParallelMandelbrot &) {
        return *this;
    };

private:
 Mat &m_img;
 float m_x1;
 float m_y1;
 float m_scaleX;
 float m_scaleY;
};
//4.示例
int main()
{
    Mat mandelbrotImg(4800, 5400, CV_8U);
    float x1 = -2.1f, x2 = 0.6f;
    float y1 = -1.2f, y2 = 1.2f;
    float scaleX = mandelbrotImg.cols / (x2 - x1);
    float scaleY = mandelbrotImg.rows / (y2 - y1);

    cv::parallel_for_(Range(0, mandelbrotImg.rows*mandelbrotImg.cols),//给定处理像素的范围
                       [&](const Range& range)//lambda函数，赋值值给函数指针functor，下面的一对大括号是lambda函数的函数体
                                             //其实我一直有个疑问，第一个参数range与[&](const Range& range)是怎么关联起来的？？？？？？？？。 
{ for (int r = range.start; r < range.end; r++) { int i = r / mandelbrotImg.cols; int j = r % mandelbrotImg.cols; float x0 = j / scaleX + x1; float y0 = i / scaleY + y1; complex<float> z0(x0, y0); uchar value = (uchar) mandelbrotFormula(z0); mandelbrotImg.ptr<uchar>(i)[j] = value; } }); string winname="mandelbrotImg"; namedWindow(winname,WINDOW_FREERATIO); imshow(winname,mandelbrotImg); waitKey(); return 0; }