C++版全连接神经网络

本程序主要包括两部分：一、神经元类NeuronNode，里面含有基本的神经元信息，比如权重w、偏置项b，输出项out_a，他们都是以矩阵的形式表示；该类可以定义一个或多个神经层，每个神经层节点组成矩阵

                                       二、神经网络类NeronNet，在该类中将NeuronNode组织成多层神经网络。

 

class NeuronNode
{
public:
    Mat z;//单个输出，将w与前一层的输出out_a相乘，并加上偏置项b
    Mat out_a;//本神经层的输出矩阵
    Mat b;
    Mat w;//后一层网络各个节点的权重
    int numOfNode;//当前层的节点数，也就是神经元的个数
    int nthOfLayer;//当前层为第n层
};

Mat sigmoid(Mat&z)//激活函数
{
    Mat temp=Mat(z.size(),z.type(),Scalar::all(0));
    for(int i=0;i<z.rows;i++)
    {
        for(int j=0;j<z.cols;j++)
        {
            float x=z.ptr<float>(i)[j];
            temp.ptr<float>(i)[j]=1/(1+exp(-x));
        }
    }
    return temp;
}
Mat sigmoid_d(Mat&z)//激活函数的微分形式
{
    Mat temp=Mat(z.size(),z.type(),Scalar::all(0));
    for(int i=0;i<z.rows;i++)
    {
        for(int j=0;j<z.cols;j++)
        {
            float x=z.ptr<float>(i)[j];
            float sig=1/(1+exp(-x));
            temp.ptr<float>(i)[j]=sig*(1-sig);
        }
    }
    return temp;
}
class NeronNet
{
public:
    NeronNet(int layer_num,vector<int> node_num_perLayer,Mat&inputMode,Mat&expectOut)
    {
        vector<int> pn=node_num_perLayer;//用一个简化指针替代原指针,只是为了方便
        if(inputMode.rows!=pn[0])
        {
            cout<<"Err: your input size !=num of node of input layer!\n";
            exit(1);
        }
        if(layer_num!=(int)pn.size())
        {
            cout<<"Err: layer_num !=num of layers from node of input layer!\n";
            exit(1);
        }
        if(numOfLayers<3)
        {
            cout<<"Err: layer_num <3!\n";
            exit(1);
        }
        this->expectOut=expectOut;
        this->totalErr=1;
        numOfLayers=layer_num;//获取层数
        nn=new NeuronNode[numOfLayers];//创建见网络层数
        nn[0].out_a=inputMode;//第1层，即nn[0]层，获取输入矢量

        cv::RNG rng;
        for(int i=1;i<numOfLayers;i++)
        {
            nn[i].b=Mat(pn[i],1,CV_32F,Scalar(0));
            nn[i].w=Mat(pn[i],pn[i-1],CV_32F,Scalar(0));//w的行数为当前层节点个数，w的列数为前一层节点个数
            //用随机数为第i层的偏移b、权重w初始化
            rng.fill(nn[i].b,RNG::UNIFORM,1,0);
            rng.fill(nn[i].w,RNG::UNIFORM,1,0);
            if(inputMode.cols>1)
            {
                int nx=inputMode.cols;
                Mat nnb;
                repeat(nn[i].b,1,nx,nnb);
                nn[i].b=nnb.clone();
            }
        }

    }

    void calcForward()
    {
        for(int i=1;i<numOfLayers;i++)
        {
            nn[i].z=(nn[i].w)*(nn[i-1].out_a)+nn[i].b;
            nn[i].out_a=sigmoid(nn[i].z);
        }
    }
    void calcBackward(float alpha)
    {

        int L=numOfLayers-1;//最后一层的角标
        Mat D[numOfLayers];//该数组表示各个神经层的反传误差，D[0]废弃
        Mat delt[numOfLayers];//计算Bias的误差，实际上就是使用D[l]的列均值
        //首先计算最后一层误差
        {
            D[L]=(nn[L].out_a-expectOut);
            D[L] =D[L].mul(sigmoid_d(nn[L].z));
            reduce(D[L],delt[L],1,REDUCE_AVG);//计算D[L]所有列的平均值
        }
        //计算中间层误差
        for(int i=1;i<L;i++)
        {
            D[L-i]=(nn[L-i+1].w.t()*D[L-i+1]).mul(sigmoid_d(nn[L-i].z));
            reduce(D[L-i],delt[L-i],1,REDUCE_AVG);//计算D[L]所有列的平均值
        }
        //更新权重和偏置

        for(int i=1;i<=L;i++)
        {
            nn[i].w=nn[i].w-alpha*D[i]*nn[i-1].out_a.t();

            if(expectOut.cols>1)
            {
                Mat del;
                repeat(delt[i],1,expectOut.cols,del);
                delt[i]=del.clone();
            }
            nn[i].b=nn[i].b-alpha*delt[i];
        }
    }
    NeuronNode *nn;
    int numOfNeuron;
    int numOfLayers;
    Mat expectOut;
    float totalErr;
};

下面是演示程序：在该程序中同时输入两个学习矢量

1,-1,

0, 1,

0,-1,

0,-1
这两个矢量的期望输出为：

 0,0,

 0,1,

 0,0,

1,0
通过学习，使得网络具有识别两个输入矢量的能力。
在本程序中，可以同时学习多个矢量，当然也可以只学习一个矢量。

下面是实例：

int main()
{
    int numOfLayer=4;
    int inNum=4;//输入矢量元素个数
    int outNum=4;//输出矢量元素个数
    int a[]={inNum,8,8,outNum};//4层网络，每层网络的神经元个数，第0层仅仅作为输入，可以不算作网络层
    vector<int> numOfNodeOfperLayer(a,a+numOfLayer);//每层节点个数

    Mat inputL=(Mat_<float>(inNum,2)<<1,-1,
                                      0, 1,
                                      0,-1,
                                      0,-1);//第0层，作为矢量输入层
    Mat epout=(Mat_<float>(inNum,2)<<0,0,
                                     0,1,
                                     0,0,
                                     1,0);//最后一层，期望输出矢量
    cout<<"expected output:"<<endl<<epout<<endl<<endl;
    NeronNet nnet(numOfLayer,numOfNodeOfperLayer,inputL,epout);
    for(int i=0;i<15000;i++)//训练网络
    {
        nnet.calcForward();
        nnet.calcBackward(0.1);
    }

cout<<"practice output:"<<endl<<nnet.nn[numOfLayer-1].out_a<<endl<<endl;

    return 0;
}

 

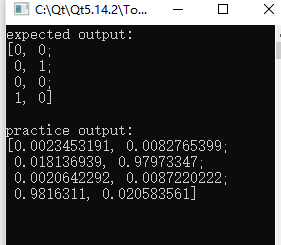
下面是输出结果：