吴恩达《深度学习》-第二门课 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)-第二周：优化算法 (Optimization algorithms) -课程笔记

第二周：优化算法 (Optimization algorithms)

2.1 Mini-batch 梯度下降（Mini-batch gradient descent）

如果训练集大小𝑚是 500 万或 5000 万或者更大的 一个数，在对整个训练集执行梯度下降法时，必须处理整个训练集，然后才能进行一步梯度下降法。所以如果在处理完整个 500 万个样本的训练集之前，先让梯度下降法处理一部分， 算法速度会更快。

batch 梯度下降法指的是之前讲过的梯度下降法算法， 就是同时处理整个训练集。 相比之下，mini-batch 梯度下降法，指的是每次同时处理的单个的 mini-batch \(𝑋^{\{𝑡\}}\) 和 \(𝑌^{\{𝑡\}}\)，而不是同时处理全部的𝑋和𝑌训练集。

mini-batch 梯度下降法的原理：

2.2 理解 mini-batch 梯度下降法（Understanding mini-batch gradient descent）

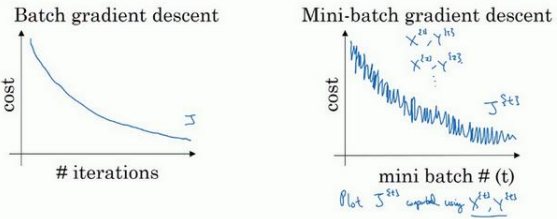
在训练中需要决定的变量之一是 mini-batch 的大小，𝑚就是训练集的大小，极端情况下:

1、如果 mini-batch 的大小等于𝑚，其实就是 batch 梯度下降法。

2、假设 mini-batch 大小为 1，就有了新的算法，叫做随机梯度下降法， 每个样本都是独立的 mini-batch。

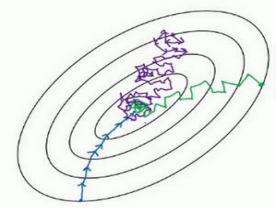
实际上选择的 mini-batch 大小在二者之间，大小在 1 和𝑚之间，而 1 太小了，𝑚太大 了，原因在于如果使用 batch 梯度下降法，mini-batch 的大小为𝑚，每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长。如果使用随机梯度下降法，如果只要处理一个样本，没有问题，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是， 会失去所有向量化带给的加速，因为一次性只处理了一个训练样本，这样效率过于低下。

2.3 指数加权平均数（Exponentially weighted averages）

之后需要使用到一些优化算法，它们比梯度下降法快，但要理解这些算法，需要用到指数加权平均，在统计中也叫做指数加权移动平均：

要做的是，

首先使\(𝑣_0 = 0\)，每天，需要使用 0.9 的加权数之前的数值加上当日温度的 0.1 倍，即\(𝑣_1 = 0.9𝑣_0 + 0.1𝜃_1\)，所以这里是第一天的温度值。

第二天，又可以获得一个加权平均数，0.9 乘以之前的值加上当日的温度 0.1 倍，即\(𝑣_2 = 0.9𝑣_1 + 0.1𝜃_2\)，以此类推。 第二天值加上第三日数据的 0.1，如此往下。

把 0.9 这个常数变成𝛽，将之 前的 0.1 变成(1 − 𝛽)，即\(𝑣_𝑡 = 𝛽𝑣_{𝑡−1} + (1 − 𝛽)𝜃_t\)。

在计算时可视\(𝑣_𝑡\)大概是 \(\frac{1}{ (1−𝛽)}\)的每日温度，将𝛽设置为接近 1 的一个值，比如 0.98，计算 1 / (1−0.98) = 50，这就是粗 略平均了一下，过去 50 天的温度，这时作图可以得到绿线。

原因在于多平均了几天的温度， 所以这个曲线，波动更小，更加平坦，缺点是曲线进一步右移，因为现在平均的温度值更多， 要平均更多的值，指数加权平均公式在温度变化时，适应地更缓慢一些，所以会出现一定延迟，因为当𝛽 = 0.98，相当于给前一天的值加了太多权重，只有 0.02 的权重给了当日的值， 所以温度变化时，温度上下起伏，当𝛽 较大时，指数加权平均值适应地更缓慢一些。

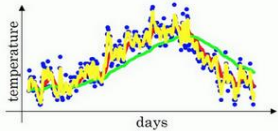
如果𝛽是另一个极端值，比如说 0.5，作图运行后得到黄线。由于仅平均了两天的温度，平均的数据太少，所以得到的曲线有更多的噪声，有可能出现异常值，但是这个曲线能够更快适应温度变化。

2.4 理解指数加权平均数（ Understanding exponentially weighted averages）

进一步地分析，来理解如何计算出每日温度的平均值。

理解𝑣100是什么？

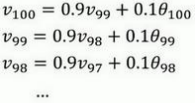
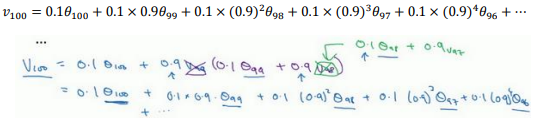
这是一个加和并平均，

所有的这些系数\(（，，，）（0.1，0.1 × 0.9，0.1 × (0.9)^2，0.1 × (0.9)^3 …）\)，相加起来为 1 或者逼近 1，我们称之为偏差修正。

需要平均多少天的温度的计算思路：

\((0.9)^{10}≈0.35\)，这个值大概是1/e，也就是说：

ε=0.1，\((1−ε)^{\frac{1}{(1−ε)}} ≈\frac{1}{e}\)大约是 0.34， 0.35，换句话说， 10 天后，曲线的高度下降到\(\frac{1}{\epsilon}\)相当于在峰值的\(\frac{1}{e}\)。

所以当β=0.9，也即ε=1−β时只关注了过去 10天的温度，因为 10 天后，权重下降到不到当日权重的三分之一。

所以估算大约平均多少天的温度时，我们使用公式：\(\frac{1}{1-\beta}\)

不过这只是思考的大致方向，并不是正式的数学证明。

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了。如果要计算移动窗，直接算出过去 10 天的总和， 过去50 天的总和，除以 10 和 50 就好，如此往往会得到更好的估测。但缺点是，如果保存所有最近的温度数据，和过去 10 天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。

2.5 指数加权平均的偏差修正（ Bias correction in exponentially weighted averages）

偏差修正，可以让平均数运算更加准确

如果在𝛽等于 0.98 的时候，得到的并不是绿色曲线，而是紫色曲线， 可以注意到紫色曲线的起点较低，来看看怎么处理。

计算移动平均数的时候，初始化\(，𝑣_0 = 0，𝑣_1 = 0.98𝑣_0 + 0.02𝜃_1\)，如果一天温度是 40 华氏度，那么\(𝑣_1 = 0.02𝜃_1 = 0.02 × 40 = 8\)，因此得到的值会小很多，所以第一天温度的估测不准。 \(𝑣_2 = 0.98𝑣_1 + 0.02𝜃_2\)，如果代入\(𝑣_1\)，然后相乘，所以 \(𝑣_2 = 0.98 × 0.02𝜃_1 + 0.02𝜃_2 = 0.0196𝜃_1 + 0.02𝜃_2\)，假设\(𝜃_1\)和\(𝜃_2\)都是正数，计算后\(𝑣_2\)要远小于𝜃1和𝜃2，所以𝑣2不能很好估测 出这一年前两天的温度。

有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用\(𝑣_𝑡\)，而是用$ \frac{𝑣_𝑡}{ 1−𝛽^𝑡}$，t 就是现在的天数。

举个具体例子，当𝑡 = 2时，\(1 − 𝛽^𝑡 = 1 − 0.982 = 0.0396\)， 因此对第二天温度的估测变成了$ \frac{𝑣_2}{ 0.0396} = \frac{0.0196𝜃_1+0.02𝜃_2}{ 0.0396} \(，也就是𝜃1和𝜃2的加权平均数，并去除了偏差。随着𝑡增加，\)𝛽^𝑡$接近于 0，所以当𝑡很大的时候，偏差修正几乎没有作用， 因此当𝑡较大的时候，紫线基本和绿线重合了。

2.6 动量梯度下降法（Gradient descent with Momentum）

一种算法叫做 Momentum，或者叫做动量梯度下降法，运行速度几乎总是快于标准的梯度下降算法，简而言之，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新权重：

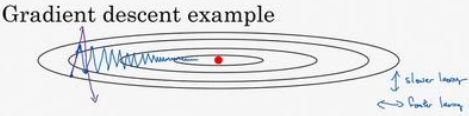
如果要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，要用一个较小的学习率。

另一个看待问题的角度是，在纵轴上，希望学习慢一点，因为不想要这些摆动，但是在横轴上，希望加快学习，希望快速从左向右移，移向最小值，移向红点。所以使用动量梯度下降法。

需要做的是，在每次迭代中，确切来说在第𝑡次迭代的过程中，计算微分𝑑𝑊，𝑑b：

计算\(𝑣_{𝑑𝑊} = 𝛽𝑣_{𝑑𝑊} +(1 − 𝛽)𝑑_𝑊\)，这跟我们之前的计算相似，也就是\(𝑣 = 𝛽𝑣 + (1 − 𝛽)𝜃_𝑡\)，𝑑𝑊的移动平均数，接 着同样地计算\(，𝑣_{𝑑𝑏}，𝑣_{𝑑𝑏} = 𝛽𝑣_{𝑑𝑏} + (1 − 𝛽)𝑑𝑏\)，然后重新赋值权重，\(𝑊: = 𝑊 − 𝑎𝑣_{𝑑𝑊}\)，同样\(𝑏: = 𝑏 − 𝑎𝑣_{𝑑𝑏}\)，这样就可以减缓梯度下降的幅度。

在上几个导数中，会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，平均过程中，正负数相互抵消，所以平均值接近于零。但在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大，因此用算法几次迭代后，动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快，算法走了一 条更加直接的路径，在抵达最小值的路上减少了摆动。

2.7 RMSprop

RMSprop 的算法， 全称是 root mean square prop 算法，它也可以加速梯度下降：

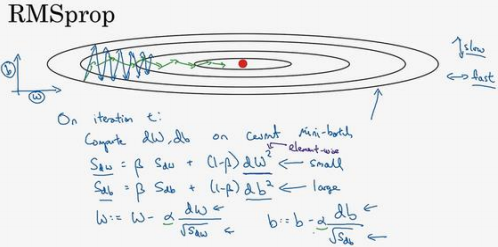
在第𝑡次迭代中，该算法会照常计算当下 mini-batch 的微分𝑑𝑊，𝑑𝑏，保留这个指数加权平均数，并用到新符号\(𝑆_{𝑑𝑊}\)，而不是\(𝑣_{𝑑𝑊}\)，因此\(𝑆_{𝑑𝑊} = 𝛽𝑆_{𝑑𝑊} + (1 − 𝛽)𝑑𝑊^2\)，这个平方的操作是针对这一整个符号的，这样做能够保留微分平方的加权平均数，同样\(𝑆_{𝑑𝑏} = 𝛽𝑆_{𝑑𝑏} + (1 − 𝛽)𝑑𝑏^2\)。

接着 RMSprop 更新参数值，\(，𝑊: = 𝑊 − 𝑎 \frac{𝑑𝑊}{\sqrt{𝑆_{𝑑𝑊} }}，𝑏: = 𝑏 − 𝛼 \frac{𝑑𝑏}{\sqrt{𝑆_{𝑑𝑏}}}\) ，其原理：

希望减缓纵轴上的摆动，所以有了\(𝑆_{𝑑𝑊}\)和\(𝑆_{𝑑𝑏}\)，希望\(𝑆_{𝑑𝑊}\)会相对较小，所以要除以一个较小的数，而希望\(𝑆_{𝑑𝑏}\)又较大，所以这里要除以较大的数字，这样就可以减缓纵轴上的变化。

这些微分，垂直方向的要比水平方向的大得多，所以斜率在𝑏方向特别大，所以这些微分中，𝑑𝑏较大，𝑑𝑊较小，因为函数的倾斜程度，在纵轴 上，也就是 b 方向上要大于在横轴上，也就是𝑊方向上。𝑑𝑏的平方较大，所以\(𝑆_{𝑑𝑏}\)也会较大， 而相比之下，𝑑𝑊会小一些，亦或𝑑𝑊平方会小一些，因此\(𝑆_{𝑑𝑊}\)会小一些，结果就是纵轴上的 更新要被一个较大的数相除，就能消除摆动，而水平方向的更新则被较小的数相除。

RMSprop 的影响就是更新最后会变成绿色线，纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，可以用一个更大学习率𝑎，然后加快学习，而无须在纵轴上垂直方向偏离。RMSprop，全称是均方根，因为将微分进行平方，然后最后使用平方根。

2.8 Adam 优化算法(Adam optimization algorithm)

Adam 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起：

Adam 算法结合了 Momentum 和 RMSprop 梯度下降法，并且是一种极其常用的学 习算法，被证明能有效适用于不同神经网络，适用于广泛的结构。

本算法中有很多超参数，超参数学习率𝑎很重要，也经常需要调试，可以尝试一系列值，然后看哪个有效。\(𝛽_1\)常用的缺省值为 0.9，这是 dW 的移动平均数，也就是𝑑𝑊的加权平 均数，这是 Momentum 涉及的项。至于超参数\(𝛽_2\)，Adam 论文作者，也就是 Adam 算法的发明者，推荐使用 0.999，这是在计算\((𝑑𝑊)^2\)以及\((𝑑𝑏)^2\)的移动加权平均值，关于𝜀的选择其实没那么重要，Adam 论文的作者建议𝜀为\(10^{−8}\)，但并不需要设置它，因为它并不会影响算法表现。

Adam 代表的是 Adaptive Moment Estimation，\(𝛽_1\)用于计算这个微分（𝑑𝑊），叫做第一矩，\(𝛽_2\)用来计算平方数的指数加权平均数\(（）（(𝑑𝑊) ^2）\)，叫做第二矩。

2.9 学习率衰减(Learning rate decay)

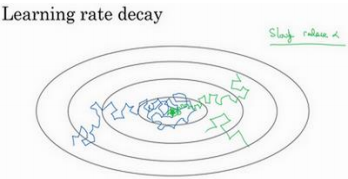
慢慢减少𝑎的本质在于，在学习初期，能承受较大的步伐，但当开始收敛的时候， 小一些的学习率能让步伐小一些。

可以将𝑎学习率设为\(𝑎 =\frac{ 1}{ 1+𝑑𝑒𝑐𝑎𝑦𝑟𝑎𝑡𝑒∗epoch−num }𝑎_0\) ( decay-rate称为衰减率，epochnum 为代数，\(𝛼_0\)为初始学习率）

比如，指数衰减，其中𝑎相当于一个小于 1 的值，如\(𝑎 = 0.95^{epoch−num}𝑎_0\)，所 以你的学习率呈指数下降。

人们用到的其它公式有\(𝑎 = \frac{𝑘}{epoch−num} 𝑎_0\)或者\(𝑎 = \frac{𝑘}{\sqrt{𝑡}}𝑎_0\)（𝑡为 mini-batch 的数字）。 有时也会用一个离散下降的学习率，也就是某个步骤有某个学习率，一会之后，学习率减少了一半，一会儿减少一半，一会儿又一半，这就是离散下降（discrete stair cease） 。

2.10 局部最优的问题(The problem of local optima)

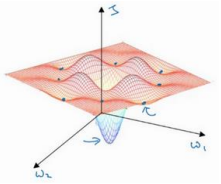
局部最优这里无过多理解。