吴恩达《深度学习》-第二门课 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)-第一周:深度学习的实践层面 (Practical aspects of Deep Learning) -课程笔记
第一周:深度学习的实践层面 (Practical aspects of Deep Learning)
1.1 训练,验证,测试集(Train / Dev / Test sets)
创建新应用的过程中,不可能从一开始就准确预测出一些信息和其他超级参数,例如:神经网络分多少层;每层含有多少个隐藏单元;学习速率是多少;各层采用哪些激活函数。应用型机器学习是一个高度迭代的过程。

从一个领域或者应用领域得来的直觉经验,通常无法转移到其他应用领域,最佳决策取决于 所拥有的数据量,计算机配置中输入特征的数量,用 GPU 训练还是 CPU,GPU 和 CPU 的具体配置以及其他诸多因素。
对于很多应用系统,即使是经验丰富的深度学习行家也不太可能一开始就预设出最匹配的超级参数,所以说,应用深度学习是一个典型的迭代过程,需要多次循环往复,才能为应用程序找到一个称心的神经网络,因此循环该过程的效率是决定项目进展速度的一个关键因素,而创建高质量的训练数据集,验证集和测试集也有助于提高循环效率。
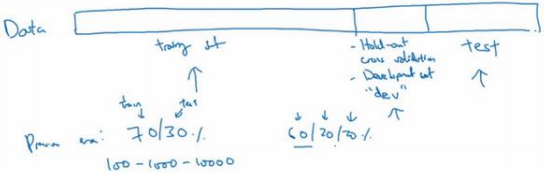
通常会将这些数据划分成几部分,一部分作为训练集,一部分作为简单交叉验证集,有时也称之为验证集(dev set)最后一部分则作为测试集。
在机器学习发展的小数据量时代,常见做法是将所有数据三七分,就是 70% 验证集,30%测试集,如果没有明确设置验证集,也可以按照60%训练,20%验证和20%测试集来划分。
在大数据时代,那么验证集和测试集占数据总量的比例会趋向于变得更小。因为验证集的目的就是验证不同的算法,检验哪种算法更有效, 因此,验证集要足够大才能评估,比如 2 个甚至 10 个不同算法,并迅速判断出哪种算法更有效。可能不需要拿出20%的数据作为验证集。验证集和测试集要小于数据总量的 20%或 10%。
根据经验,建议要确保验证集和测试集的数据来自同一分布。因为要用验证集来评估不同的模型,尽可能地优化性能。 如果验证集和测试集来自同一个分布就会很好。
最后一点,就算没有测试集也不要紧,测试集的目的是对最终所选定的神经网络系统做出无偏估计,如果不需要无偏估计,也可以不设置测试集。
1.2 偏差,方差(Bias /Variance)
过拟合、欠拟合概念
欠拟合:不能很好地拟合数据,是高偏差(high bias)的情况
过拟合:方差较高(high variance)
适度拟合(just right):介于过度拟合和欠拟合 中间的一类
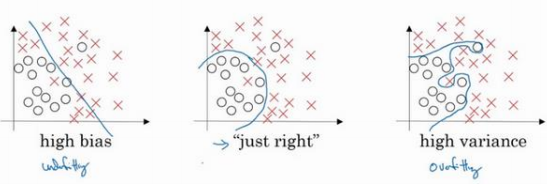
“高方差”:
假定训练集误差是 1%,验证集误差是 11%,训练集设置得非常好,而验证集设置相对较差,可能过度拟合了训练集,在某种程度上,验证集并没有充分利用交叉验证集的作用
“高偏差”:
假设训练集误差是 15%,验证集误差是 16%,人的错误率几乎为 0%,算法并没有在训练集中得到很好训练,训练数据的拟合度不高,就是数据欠拟合,就可以说这种算法偏差比较高。
它对于验证集产生的结果却是合理的,验证集中的错误率只比训练集的多了 1%,但这种算法偏差高,因为它甚至不能拟合训练集。
高、低|方差和偏差:
训练集误差是 15%,偏差相当高,但是,验证集的评估结果更糟糕,错误率达到 30%,在这种情况下,会认为这种算法偏差高,因为它在训练集上结果不理想, 而且方差也很高,这是方差偏差都很糟糕的情况。
训练集误差是 0.5%,验证集误差是 1%,只有 1%的错误率,偏差和方差都很低。
以上分析的前提都是假设基本误差很小,训练集和验证集数据来自相同分布,如果没有这些假设作为前提,分析过程更加复杂。
如果稍微改变一下分类器,它会过度拟合部分数据,用紫色线画出的分类器具有高偏差和高方差,偏差高是因为它几乎是一条线性分类器,并未拟合数据。而采用曲线函数或二次元函数会产生高方差,因为它曲线灵活性太高以致拟合了这两个错误样本和中间这些活跃数据。
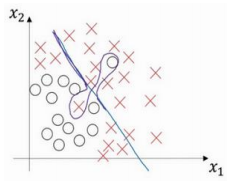
对于高维数据,有些数据区域偏差高,有些数据区域方差高。在高维数据中采用这种分类器看起来就不会那么牵强了
在训练集上训练算法产生的误差和验证集上验证算法产生的误差来诊断算法是否存在高偏差和高方差,是否两个值都高,或者两个值都不高,根据算法偏差和方差的具体情况决定接下来要做的工作。
1.3 机器学习基础(Basic Recipe for Machine Learning)
在训练神经网络时用到的基本方法:
初始模型训练完成后,首先要知道算法的偏差高不高,如果偏差较高,试着评估训练集或训练数据的性能。如果偏差的确很高,甚至无法拟合训练集,那么要做的就是选择一个新的网络,比如含有更多隐藏层或者隐藏单元的网络,或者花费更多时间来训练网络,或者尝试更先进的优化算法。也可以尝试其他方法,可能有用,也可能没用。
不过采用规模更大的网络通常都会有所帮助,延长训练时间不一定有用,但也没什么坏处。训练学习算法时,不断尝试这些方法,直到解决掉偏差问题,这是最低标准,反复尝试,直到可以拟合数据为止,至少能够拟合训练集。
一旦偏差降低到可以接受的数值,检查一下方差有没有问题,为了评估方差,要查看验证集性能,如果方差高,最好的解决办法就是采用更多数据,但有时候,无法获得更多数据。也可以尝试通过正则化来减少过拟合。总之就是不断重复尝试,直到找到一个低偏差,低方差的框架,这时就成功了。
有两点需要注意:
第一点,高偏差和高方差是两种不同的情况,后续要尝试的方法也可能完全不同, 通常会用训练验证集来诊断算法是否存在偏差或方差问题,然后根据结果选择尝试部分方 法。
第二点,在机器学习的初期阶段,能尝试的方法有很多。可以增加偏差,减少方差,也可以减少偏差,增加方差,但是在深度学习的早期阶段,没有太多工具可以做到只减少偏差或方差却不影响到另一方。但在当前的深度学习和大数据时代,只要正则适度,通常构建一个更大的网络便可以,在不影响方差的同时减少偏差,而采用更多数据通常可以在不过多影响偏差的同时 减少方差。
1.4 正则化(Regularization)
深度学习可能存在过拟合问题——高方差,有两个解决方法,一个是正则化,另一个是准备更多的数据。正则化有助于避免过度 拟合,或者减少网络误差:
在逻辑回归函数中加入正则化:
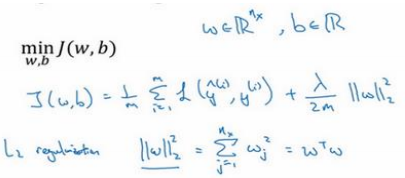
此方法称为𝐿2正则化。
因为𝑤通常是一个高维参数矢量,已经可以表达高偏差问题,𝑤可能包含有很多参数, 我们不可能拟合所有参数,而𝑏只是单个数字,所以𝑤几乎涵盖所有参数,而不是𝑏,如果加了参数𝑏,其实也没太大影响,因为𝑏只是众多参数中的一个,所以通常省略不计,如果加上这个参数,完全没问题。
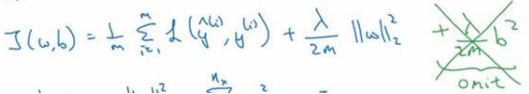
𝐿1正则化,加的不是𝐿2 范数,而是正则项:\(\frac{\lambda}{m}\sum_{j=1}^{n_x}|w|\)
如果用的是𝐿1正则化,𝑤最终会是稀疏的,也就是说𝑤向量中有很多 0,虽然𝐿1正则化使模型变得稀疏,却没有降低太多存储内存,所以这并不是𝐿1正则化的目的,至少不是为了压缩模型,倾向于使用𝐿2正则化。
𝜆是正则化参数,通常使用验证集或交叉验证集来配置这 个参数,不断尝试,寻找最好的参数,把参数设置为较小值,这样可以避免过拟合。
为了方便写代码,在 Python 编程语言中,𝜆是一个保留字段,编写代码时, 成𝑙𝑎𝑚𝑏𝑑,以免与 Python 中的保留字段冲突。
神经网络中的𝐿2正则化:
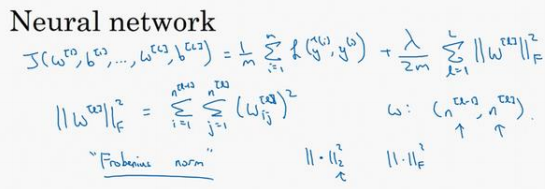
正则项为:\(\frac{\lambda}{2m}\sum_1^L||W^{[l]}||^2\)
这个矩阵范数\(||W^{[l]}||^2\)(即平方范数),被定义为矩阵中所有元素的平方求和。
𝑊是一个\(𝑛^{[𝑙]} × 𝑛^{[𝑙−1]}\)的多维矩阵,\(𝑛^{[𝑙]}\)表示𝑙 层单元的数量,\(𝑛^{[𝑙−1]}\)表示第𝑙 − 1层隐 藏单元的数量。
该矩阵范数被称作“Frobenius范数”,用下标𝐹标注,鉴于线性代数中一些神秘晦涩的原因,不称之为“矩阵𝐿2范数”,而称它为“Frobenius范数。
使用该范数实现梯度下降:

\(𝑊^{[𝑙]}\)的定义被更新为\(𝑊^{[𝑙]}\)减去学习率 𝑎 乘以 backprop 再加上\(\frac{\lambda}{m}W^{[l]}\)
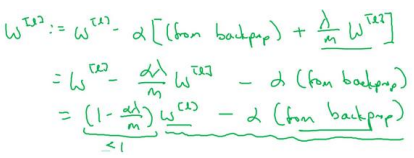
该正则项说明,不论\(𝑊^{[𝑙]}\)是什么,我们都试图让它变得更小,相当于我们给矩 阵 W 乘以(\(1 − 𝑎 \frac{\lambda}{m}\) )倍的权重,该系数小于 1,因此𝐿2范数正则化也被称为“权重衰减”。
1.5 为什么正则化有利于预防过拟合呢?(Why regularization reduces overfitting?)
一、直观上理解就是如果正则化𝜆设置得足够大,权重矩阵𝑊被设置为接近于0 的值,直观理解就是把多隐藏单元的权重设为 0,于是基本上消除了这些隐藏单元的许多影响。如果是这种情况,这个被大大简化了的神经网络会变成一个很小的网络,小到如同一个逻辑回归单元,可是深度却很大,它会使这个网络从过度拟合的状态更接近高偏差状态。
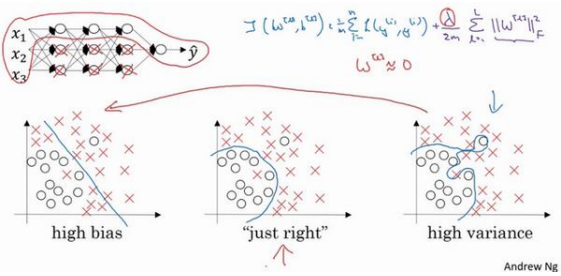
但是𝜆会存在一个中间值,于是会有一个接近“Just Right”的中间状态。
实际上是该神经网络的所有隐藏单元依然存在,但是它们的影响变得更小了。神经网络变得更简单了,不确定这个直觉经验是否有用,不过在编程中执行正则化时, 实际看到一些方差减少的结果。
二、如果𝑊很小,相对来说,𝑧也会很小。特别是,如果𝑧的值最终在这个范围内,都是相对较小的值,𝑔(𝑧)大致呈线性,每层几乎都是线性的,和线性回归函数一样。如果每层都是线性的,那么整个网络就是一个线性网络,即使是一个非常深的深层网络,因具有线性激活函数的特征,最终我们只能计算线性函数,因此,它不适用于非常复杂的决策,以及过度拟合数据集的非线性决策边界。
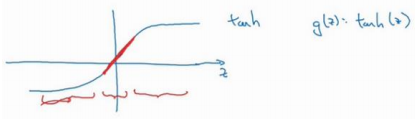
总结一下,如果正则化参数变得很大,参数𝑊很小,𝑧也会相对变小,此时忽略𝑏的影响, 𝑧会相对变小,实际上,𝑧的取值范围很小,这个激活函数,也就是曲线函数𝑡𝑎𝑛ℎ会相对呈线性,整个神经网络会计算离线性函数近的值,这个线性函数非常简单,并不是一个极复杂的高度非线性函数,不会发生过拟合。
1.6 dropout 正则化(Dropout Regularization)
dropout 会遍历网络的每一层,并设置消除神经网络中节点的概率。设置完节点概率,我们会消除一些节点,然后删除掉从该节点进出的连线,最后得到一个节点更少,规模更小的网络,然后用 backprop 方法进行训练。
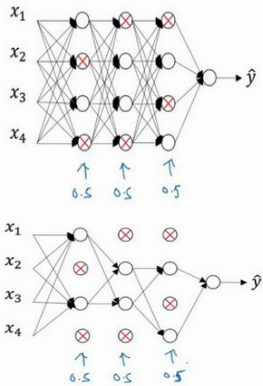
实施 dropout 最常用的方法: inverted dropout(反向随机失活)
只举例说明如何在某一层中实施 dropout:
首先要定义向量𝑑,\(𝑑^{[3]}\)表示一个三层的 dropout 向量:
d3 = np.random.rand(a3.shape[0],a3.shape1)
此处 keep-prob 等于 0.8, 它意味着消除任意一个隐藏单元的概率是 0.2,它的作用就是生成随机矩阵。\(𝑑^{[3]}\)是一个矩阵,其中\(𝑑^{[3]}\)中的对应值为 1 的概率都是 0.8,对应为 0 的概率是 0.2,随机数字小于 0.8。它等于 1 的概率是 0.8, 等于 0 的概率是 0.2。
接下来要做的就是从第三层中获取激活函数,这里我们叫它\(𝑎^{[3]}\): a3 =np.multiply(a3,d3),这里是元素相乘。它的作用就是让\(𝑑^{[3]}\)中所有等于 0 的元素(输出),而各个元素等于 0 的概率 只有 20%,乘法运算最终把\(𝑑^{[3]}\)中相应元素输出,即让\(𝑑^{[3]}\)中 0 元素与\(a^{[3]}\)中相对元素归零。

用 python 实现该算法的话,𝑑 [3]则是一个布尔型数组,值为 true 和 false,而不是 1 和 0,乘法运算依然有效,python 会把 true 和 false 翻译为 1 和 0。
最后,我们向外扩展\(𝑎^{[3]}\),用它除以 0.8,或者除以 keep-prob 参数。
𝑎3/= 𝑘𝑒𝑒𝑝 − 𝑝𝑟𝑜b
解释一下为什么要这么做:
假设第三隐藏层上有 50 个单元,在一维上\(𝑎^{[3]}\)是 50,保留和删除它们的概率分别为 80%和 20%:\(𝑧^{[4]}:𝑧^{[4]} = 𝑤^{[4]}𝑎^{[3]} + 𝑏^{[4]}\),为了不影响\(𝑧^{[4]}\)的期望值,我们需要用\(𝑤^{[4]}𝑎^{[3]}/0.8\),它将会修正或弥 补我们所需的那 20%,\(𝑎^{[3]}\)的期望值不会变。Dropout 早期的迭代版本都没有除以 keep-prob,所以在测试阶段,平均值会变得越来越复杂。
在测试阶段进行预测时,我们不期望输出结果是随机的,并未使用 dropout。
1.7 理解 dropout(Understanding Dropout)
直观上理解:
不要依赖于任何一个特征,因为该单元的输入可能随时被清除,因此该单元通过这种方式传播下去,并为单元的四个输入增加一点权重,通过传播所有权重,dropout 将产生收缩权重的平方范数的效果,和之前讲的𝐿2正则化类似;实施 dropout 的结果实它会压缩权重,并完成一些预防过拟合的外层正则化;𝐿2对不同权重的衰减是不同的,它取决于激活函数倍增的大小。
总结一下,dropout 的功能类似于𝐿2正则化,与𝐿2正则化不同的是,被应用的方式不同, dropout 也会有所不同,甚至更适用于不同的输入范围。
实施 dropout 的另一个细节是,这是一个拥有三个输入特征的网络,其中一个要选择的 参数是 keep-prob,它代表每一层上保留单元的概率。所以不同层的 keep-prob 也可以变化。
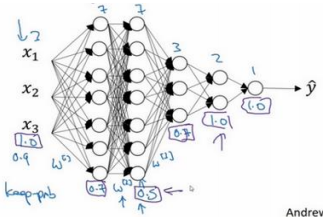
对于有可能出现过拟合,且含有诸多参数的层,我们可以把 keep-prob 设置成比较小的值,以便应用更强大的 dropout
总结一下,如果你担心某些层比其它层更容易发生过拟合,可以把某些层的 keep-prob 值设置得比其它层更低,缺点是为了使用交叉验证,要搜索更多的超级参数,另一种方案是在一些层上应用 dropout,而有些层不用 dropout,应用 dropout 的层只含有一个超级参数,就是 keep-prob。
要牢记一点,dropout 是一种正则化方法,它有助于预防过拟合,因此除非算法过拟合,不然是不会使用 dropout 的,所以它在其它领域应用得比较少,主要存在于计算机视觉领域,因为我们通常没有足够的数据,所以一直存在过拟合。
dropout 一大缺点就是代价函数𝐽不再被明确定义,每次迭代,都会随机移除一些节点,在某种程度上很难计算,所以失去了调试工具来绘制这样的图片。通常会关闭 dropout 函数,将 keepprob 的值设为 1,运行代码,确保𝐽函数单调递减。然后打开 dropout 函数,希望在 dropout 过程中,代码并未引入 bug。
1.8 其他正则化方法(Other regularization methods)
一.数据扩增
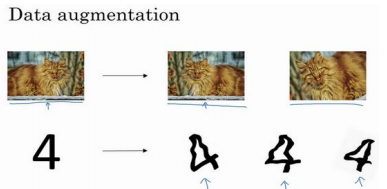
二.early stopping
通过 early stopping,不但可以绘制训练内容,还可以绘制验证集误差,它可以是验证集上的分类误差,或验证集上的代价函数,逻辑损失和对数损失等,验证集误差通常会先呈下降趋势, 然后在某个节点处开始上升。
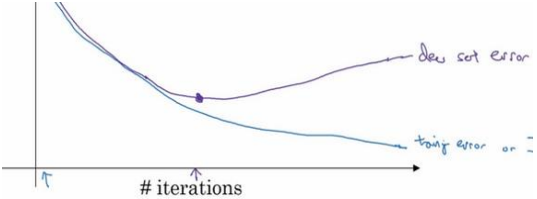
early stopping 要做就是在中间点停止迭代过程,我们得到一个𝑤值中等大小的弗罗贝尼乌斯范数,与𝐿2正则化相似,选择参数𝑤范数较小的神经网络,但愿神经网络过度拟合不严重。
early stopping 的主要缺点就是不能独立地处理两个问题,因为提早停止梯度下降,也就是停止了优化代价函数。
Early stopping 的优点是,只运行一次梯度下降,可以找出𝑤的较小值,中间值和较大值,而无需尝试𝐿2正则化超级参数𝜆的很多值。
1.9 归一化输入(Normalizing inputs)
训练神经网络,其中一个加速训练的方法就是归一化输入。
1.零均值
2.归一化方差
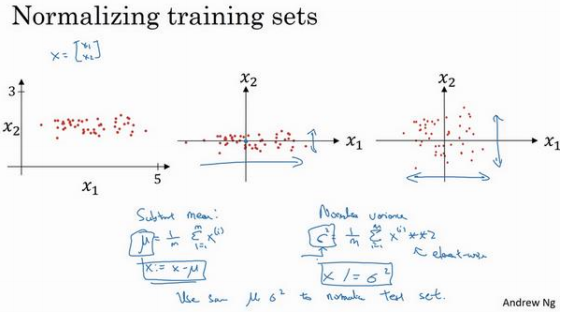
第一步是零均值化:\(\mu=\frac{1}{m}\sum_{i=1}^mx^{(i)}\),𝑥等于每个训练数据 𝑥减去 \(\mu\)
第二步是归一化方差:注意特征𝑥1的方差比特征𝑥2的方差要大得多,第一步已经完成零值均化,\((𝑥^{(𝑖)} )^ 2\)元素\(𝑦^2\)就是方差。\(\sigma^2=\frac{1}{m}\sum_{i=1}^m(x^{(1)})^2\),把所有数据除以向量 \(\sigma^2\),最后变成右图一的形式。
不希望训练集和测试集的归一化有所不同,所以要用同样的方法调整测试集, 而不是在训练集和测试集上分别预估𝜇 和 \(\sigma^2\) 。
为什么要归一化输入特征:
非归一化的输入特征:
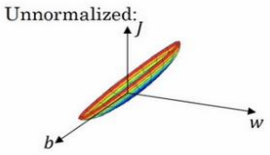
然而如果归一化特征,代价函数平均起来看更对称:否则必须使用一个非常小的学习率
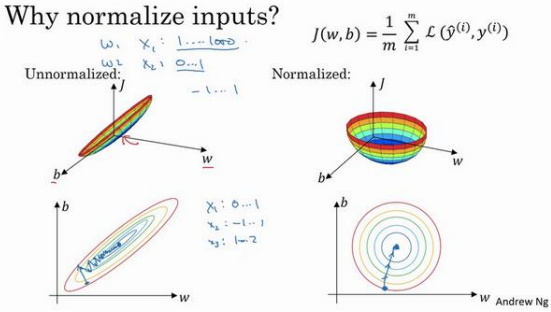
但如果函数是一个更圆的球形轮廓,那么不论从哪个位置开始,梯度下降法都能够更直接地找到最小值。
在-1 到 1 范围内或相似偏差,这使得代价函数𝐽优化起来更简单快速。
实际上如果假设特征𝑥1范围在 0-1 之间,𝑥2的范围在-1 到 1 之间,𝑥3范围在 1-2 之间, 它们是相似范围,所以会表现得很好。确保所有特征都在相似范围内,通常可以帮助学习算法运行得更快。
1.10 梯度消失/梯度爆炸(Vanishing / Exploding gradients)
训练神经网络,尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸:

假设每个权重矩阵\(W^{[l]}=\begin{bmatrix}1.5&0\\0&1.5\\\end{bmatrix},y=W^{[l]}\begin{bmatrix}1.5&0\\0&1.5\\\end{bmatrix}^{(l-1)}\)𝐿值较大,𝑦的值将爆炸式增长。相反,如果\(W^{[l]}=\begin{bmatrix}0.5&0\\0&0.5\\\end{bmatrix}\),激活函数以指数级递减。在这样一个深度神经网络中,如果激活函数或梯度函数以与𝐿相关的指数增长或递减,它们的值将会变得极大或极小,从而导致训练难度上升。
1.11 神经网络的权重初始化(Weight Initialization for Deep Networks)
\(𝑧 = 𝑤_1𝑥_1 + 𝑤_2𝑥_2 + ⋯ + 𝑤_𝑛𝑥_n,b=0\)
为了预防𝑧值过大或过小,𝑛越大,希望\(𝑤_𝑖\)越小,最合理的方法就是设置 \(w_i=\frac{1}{n}\),
实际上,要做的就是设置某层权重矩阵:
\(n^{l-1}\)即第𝑙 − 1层神经元数量
如果用的是 Relu 激活函数:
方差设置为\(\frac{2}{n}\) ,效果会更好
tanh 激活函数:常量 1 比常量 2 的效率更高
1.12 梯度的数值逼近(Numerical approximation of gradients)
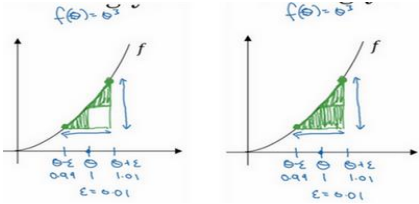
有时候,虽然写下了方程式,却不能 100%确定,执行 backprop 的所有细节都是 正确的。使用梯度检验确保 backprop 正确实施。梯度检验前需要理解计算梯度的数值逼近:
采用双边公差的方法更逼近导数:𝑓(𝜃 + 𝜀) − 𝑓(𝜃 − 𝜀),\(\frac{f(\theta+\epsilon)-f(\theta-\epsilon)}{2\epsilon}\)
1.13 梯度检验(Gradient checking)
梯度检验可以帮助节省很多时间和发现 backprop 实施过程中的bug:

实施梯度检验的过程,通常简称为“grad check”:
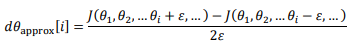
之后要做的就是验证向量 \(d\theta\) 和 \(d\theta_{approx}\) 是否彼此接近。
定义两个向量是否接近:一般计算这两个向量的距离,\(𝑑𝜃_{approx}[𝑖] − 𝑑𝜃[𝑖]\)的欧几里得范数。注意这里(\(||𝑑𝜃_{approx} − 𝑑𝜃||_2\))没有平方,它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数,分母只是用于预防这些向量太小或太大,分母使得这个方程式变成比率。

1.14 梯度检验应用的注意事项(Gradient Checking Implementation Notes)

首先,不要在训练中使用梯度检验,它只用于调试。计算所有𝑖值的 \(𝑑𝜃_{approx}[𝑖]\)是一个非常漫长的计算过程。
第二点,如果算法的梯度检验失败,要检查所有项,检查每一项,并试着找出bug。
第三点,在实施梯度检验时,如果使用正则化,请注意不要忘了正则项。
第四点,梯度检验不能与 dropout 同时使用,因为每次迭代过程中,dropout 会随机消除隐藏层单元的不同子集,难以计算 dropout 在梯度下降上的代价函数𝐽。建议关闭 dropout,用梯度检验进行双重检查,在没有 dropout 的情况下,算法至少是正确的,然后打开 dropout。
最后一点,现实中几乎不会出现这种情况。当𝑤和𝑏接近 0 时, 梯度下降的实施是正确的,,但是在运行梯度下降时,𝑤和𝑏变得更大。可能只有在𝑤和𝑏接近 0 时,backprop 的实施才是正确的。但是当𝑊和𝑏变大时,它会变得越来越不准确。不常用的一种方法:就是在随机初始化过程中,运行梯度检验,然后再训练网络,𝑤和𝑏会有一段时间远离 0,如果随机初始化值比较小,反复训练网络之后,再重新运行梯度检验。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号