吴恩达《深度学习》-第一门课 (Neural Networks and Deep Learning)-第四周:深层神经网络(Deep Neural Networks)-课程笔记
第四周:深层神经网络(Deep Neural Networks)
4.1 深层神经网络(Deep L-layer neural network)
有一些函数,只有非常深的神经网络能学会,而更浅的模型则办不到。
对于给定的问题很难去提前预测到底需要多深的神经网络,所以先去尝试逻辑回归,尝试一层然后两层隐含层, 然后把隐含层的数量看做是另一个可以自由选择大小的超参数,然后再保留交叉验证数据上 评估,或者用开发集来评估。
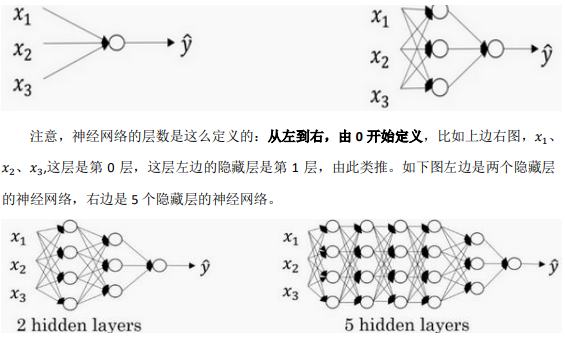
一些符号注意:
用 L 表示层数,上图5hidden layers :𝐿 = 6,输入层的索引为“0”,第一个隐藏层\(n^{[1]}\) = 4,表示有 4 个隐藏神经元,同理$𝑛^{[2]} \(= 4......\)n^{ [𝐿]} = 1\((输出单元为 1)。而输入层,\)𝑛^{[0]} = 𝑛_𝑥 = 3$。
4.2 深层网络中的前向传播(Forward propagation in a Deep Network)

前向传播可以归纳为多次迭代\(,。𝑧^{[𝑙]} = 𝑤^{[𝑙]}𝑎^{[𝑙−1]} + 𝑏^{[𝑙]},𝑎^{[𝑙]} = 𝑔^{[𝑙]}(𝑧^{[𝑙]} )。\)
4.3 核对矩阵的维数(Getting your matrix dimensions right)
在做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率
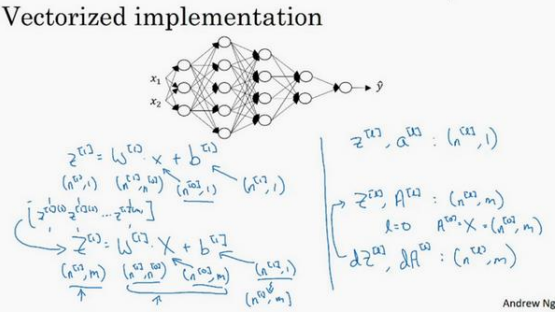
𝑤的维度是(下一层的维数,前一层的维数),即\(𝑤^{[𝑙]} : (𝑛^{[𝑙]} ,𝑛^{[𝑙−1]} )\)
𝑏的维度是(下一层的维数,1)
\(和𝑑𝑤^{[𝑙]}和𝑤^{[𝑙]}\)维度相同,\(𝑑𝑏^{[𝑙]}\)和\(𝑏^{[𝑙]}\)维度相同,且𝑤和𝑏向量化维度不变,但𝑧,𝑎以及𝑥的维 度会向量化后发生变化
向量化后:
\(𝑍^{[𝑙]}\)可以看成由每一个单独的\(𝑍^{[𝑙]}\)叠加而得到,\(,,,,𝑍^{[𝑙]} = (𝑧^{[𝑙][1]},𝑧^{[𝑙][2]},𝑧^{[𝑙][3]},…,𝑧^{[𝑙][𝑚]} )\), 𝑚为训练集大小,所以\(𝑍^{[𝑙]}\)的维度不再是(\(𝑛^{[𝑙]}\) , 1),而是(\(𝑛^{[𝑙]}\) , 𝑚)。 \(:,𝐴^{[𝑙]}:(𝑛^{[𝑙]} , 𝑚),𝐴^{[0]} = 𝑋 = (𝑛^{[𝑙]} , 𝑚)\)
4.4为什么使用深层表示?(Why deep representations?)
深度网络在计算什么:

举个例子,这个小方块(第一行第一列)就是一个隐藏单元,它会去找这张照片里“|”边缘的 方向。那么这个隐藏单元(第四行第四列),可能是在找(“—”)水平向的边缘在哪里。然后它可以把被探测到的边缘组合成面部的不同 部分(第二张大图)。比如说,可能有一个神经元会去找眼睛的部分,另外还有别的在找鼻 子的部分,然后把这许多的边缘结合在一起,就可以开始检测人脸的不同部分。最后再把这 些部分放在一起,比如鼻子眼睛下巴,就可以识别或是探测不同的人脸(第三张大图)。
主要的概念是,一般你会从比较小的细节入手,比如边缘,然后再一步步到更大更复杂的区域,比如一只眼睛或是一个鼻子,再把眼睛鼻子装一块 组成更复杂的部分。
这种从简单到复杂的金字塔状表示方法或者组成方法,也可以应用在图像或者人脸识别以外的其他数据上。比如建一个语音识别系统的时候。深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。
另一个关于神经网络为何有效的理论,来源于电路理论:
根据不同的基本逻辑门,譬如与门、或门、非门。在非正式 的情况下,这些函数都可以用相对较小,但很深的神经网络来计算,小在这里的意思是隐藏单元的数量相对比较小,但是如果你用浅一些的神经网络计算同样的函数,也就是说在我们不能用很多隐藏层时,你会需要成指数增长的单元数量才能达到同样的计算结果。
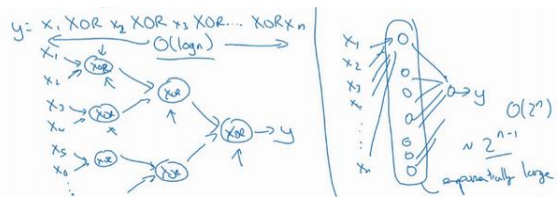
因为本质上来说你需要列举耗尽\(2^𝑛\)种可能的配置,或是\(2^𝑛\)种输入比特的配置。异或运算的最终结果是 1 或 0,那么你最终就会需要一个隐藏层,其中单元数目随输入比特指数上升。精确的说应该是\(2^{𝑛−1}\)个隐藏单元数,也就是𝑂(\(2^𝑛\) )。
4.5 搭建神经网络块(Building blocks of deep neural networks)
在第𝑙层有参数:\(𝑊^{[𝑙]}\)和\(𝑏^{[𝑙]}\)
正向传播:输入是前一层\(𝑎^{[𝑙−1]}\),输出是\(𝑎^{[𝑙]}\)
\(𝑧^{[𝑙]} = 𝑊^{[𝑙]}𝑎^{[𝑙−1]} + 𝑏^{[𝑙]} ,𝑎^{[𝑙]} = 𝑔^{[𝑙]} (𝑧^{[𝑙]} )\) 可以把$的值缓存起来,因为缓存的𝑧^{[𝑙]}的值缓存起来,因为缓存的 $$𝑧^{[𝑖]}$对以后的正向反向传播的步骤非常有用。
反向传播:
第𝑙层的计算:需要实现一个输入为\(𝑑𝑎^{[𝑙]}\),输出\(𝑑𝑎^{[𝑙−1]}\)的函数。
一个小细节需要注意:输入在这里其实是\(𝑑𝑎^{[𝑙]}\)以及所缓存 的\(𝑧^{[𝑙]}\)值
输出除了\(𝑑𝑎^{ [𝑙−1]}\)的值以外,也需要输出梯度\(𝑑𝑊^{[𝑙]}\)和 \(𝑑𝑏^{ [𝑙]}\),以实现梯度下降学习
(用红色箭头标注标注反向步骤)
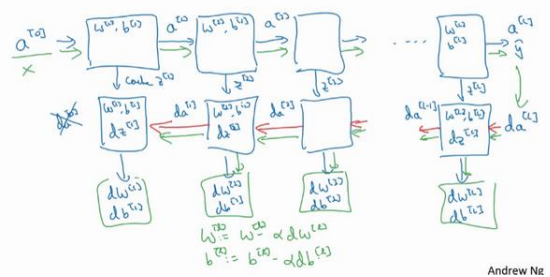
𝑊会在每一层被更新为𝑊 = 𝑊 − 𝛼𝑑𝑊,𝑏也一样,𝑏 = 𝑏 − 𝛼𝑑𝑏
4.6 前向传播和反向传播(Forward and backward propagation)
前向传播:

输入\(𝑎^{[𝑙−1]}\),输出是\(𝑎^{[𝑙]}\),缓存为\(𝑧^{[𝑙]}\);从实现的角度来说我们可以缓存下 \(𝑤^{[𝑙]}\)和\(𝑏^{[𝑙]}\),这样更容易在不同的环节中调用函数
前向传播需要喂入\(𝐴^{[0]}\)也就是𝑋,来初始化;初始化的是第一层的输入值。\(𝑎^{[0]}\)对应于一 个训练样本的输入特征,而\(𝐴^{[0]}\)对应于一整个训练样本的输入特征
反向传播:

反向传播的步骤可以写成:
向量化实现过程可以写成:
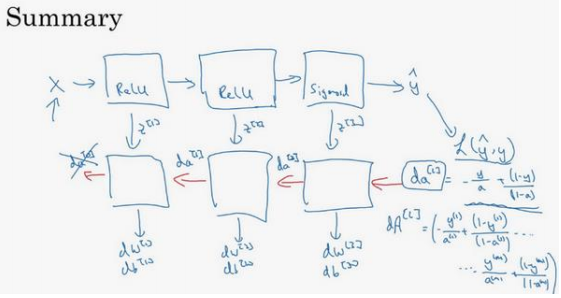
第一层可能有一个 ReLU 激活函数,第二层为另一个 ReLU 激活函数,第三层可能是 sigmoid 函数(如果做二分类的话),输出值为 $ \hat{y} $,用来计算损失;之后就可以向后迭代进行反向传播求导。
4.7 参数 VS 超参数(Parameters vs Hyperparameters)
超参数:
比如算法中的 learning rate 𝑎(学习率)、iterations(梯度下降法循环的数量)、𝐿(隐藏 层数目)、\(𝑛^{[𝑙]}\)(隐藏层单元数目)、choice of activation function(激活函数的选择)都需要手动设置,这些数字实际上控制了最后的参数𝑊和𝑏的值,所以它们被称作超参数。
深度学习有很多不同的超参数,如 momentum、mini batch size、regularization parameters 等等。
如何寻找超参数的最优值:
走 Idea—Code—Experiment—Idea 这个循环,尝试各种不同的参数,实现模型并观察是否成功,然后再迭代。
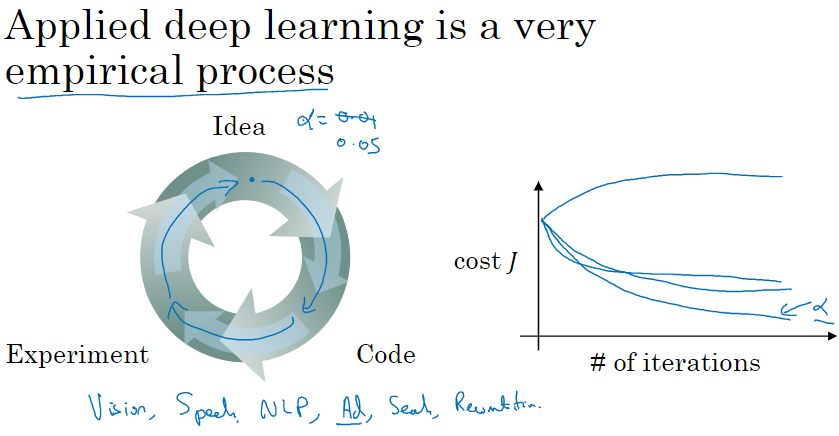
参数设定这个领域,深度学习研究还在进步中,所以可能过段时间就会有更好的方法决定超参数的值,也很有可能由于 CPU、GPU、网络和数据都在变化,这样的指南可能只会在一 段时间内起作用,只要不断尝试,并且尝试保留交叉检验或类似的检验方法,然后挑一个对问题效果比较好的数值
4.8 深度学习和大脑的关联性(What does this have to do with the brain?)

一个神经网络的逻辑单元可以看成是对一个生物神经元的过度简化,但迄今为止连神经 科学家都很难解释究竟一个神经元能做什么,它可能是极其复杂的;它的一些功能可能真的 类似 logistic 回归的运算,但单个神经元到底在做什么目前还没有人能够真正可以解释。
一个小小的神经元其 实却是极其复杂的,以至于我们无法在神经科学的角度描述清楚,它的一些功能,可能真的 是类似 logistic 回归的运算,但单个神经元到底在做什么,目前还没有人能够真正解释,大 脑中的神经元是怎么学习的,至今这仍是一个谜之过程。到底大脑是用类似于后向传播或是 梯度下降的算法,或者人类大脑的学习过程用的是完全不同的原理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号