吴恩达《深度学习》-第一门课 (Neural Networks and Deep Learning)-第三周：浅层神经网络(Shallow neural networks) -课程笔记

第三周：浅层神经网络(Shallow neural networks)

3.1 神经网络概述（Neural Network Overview）

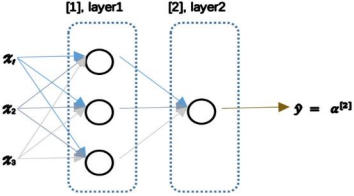
使用符号$ ^{[𝑚]}$表示第𝑚层网络中 节点相关的数，这些节点的集合被称为第𝑚层网络。

【1】初始：前向：

\[\left.\begin{aligned}𝑥\\𝑊^{[1]}\\𝑏^{[1]}\end{aligned}\right\} \Longrightarrow 𝑧^{[1]} = 𝑊^{[1]}𝑥 + 𝑏^{[1]} \Longrightarrow 𝛼^{[1]} = 𝜎(𝑧^{[1]}) \]

计算梯度

\[\left.\begin{aligned}𝑥\\𝑑𝑊^{[1]}\\𝑑𝑏^{[1]}\end{aligned}\right\} ⟸ 𝑑𝑧^{[1]} = 𝑑(𝑊^{[1]}𝑥 + 𝑏^{[1]}) ⟸ 𝑑𝛼^{[1]} = 𝑑𝜎(𝑧^{[1]}) \]

【2】第二层：类似只不过x=\(a^{[1]}\)：

\[\left.\begin{aligned}da^{[1]}=d\sigma(z^{[1]})\\𝑑𝑊^{[2]}\\𝑑𝑏^{[2]}\end{aligned}\right\} ⟸ 𝑑𝑧^{[2]} = 𝑑(𝑊^{[2]}\alpha^{[1]} + 𝑏^{[2]}) ⟸ 𝑑𝛼^{[2]} = 𝑑𝜎(𝑧^{[2]})\Longleftarrow dL(a^{[2]},y) \]

在逻辑回归中，通过直接计算𝑧得 到结果𝑎。而这个神经网络中，我们反复的计算𝑧和𝑎，计算𝑎和𝑧，最后得到了最终的输出 loss function。

3.2 神经网络的表示（Neural Network Representation）

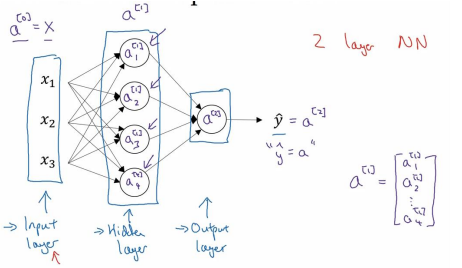
输入层：\(x_1,x_2,x_3\)

隐藏层 hidden layer 有两个参数\(W,b\)，\(^{[1]}(W^{[1]},b^{[1]})\)表示这些参数是和第一层隐藏层有关。𝑊是一个 4x3 的矩阵，而𝑏是一个 4x1 的向量

输出层 output layer 负责产生预测值

因为不将输入层看作一个标准的层，故而称为一个两层的神经网络。

3.3 计算一个神经网络的输出（Computing a Neural Network's output）

神经元的计算与逻辑回归一样分为两步：

第一步，计算\(𝑧_1^{[1]} , 𝑧_1{[1]} = 𝑤_1^{[1]𝑇}𝑥+𝑏_1^{[1]}\)。

第二步，通过激活函数计算\(𝑎_1^{[1]} , 𝑎_1^{[1]} = 𝜎(𝑧_1^{[1]})\)。

隐藏层的第二个以及后面两个神经元的计算过程一样，只是注意符号表示不同

向量化计算：

\[𝑎^{[1]} = \left[\begin{aligned} 𝑎_1^{[1]}\\ 𝑎_2^{[1]}\\ 𝑎_3^{[1]}\\ 𝑎_4^{[1]}\end{aligned}\right] = 𝜎(𝑧^{[1]} ) \]

\[\left[ \begin{aligned}𝑧_1^{[1]}\\𝑧_2^{[1]}\\𝑧_3^{[1]}\\𝑧_4^{[1]}\end{aligned}\right]=\overbrace{\left[ \begin{aligned}\cdots 𝑊_1^{[1]𝑇} \cdots\\\cdots 𝑊_2^{[2]𝑇} \cdots\\\cdots 𝑊_3^{[3]𝑇} \cdots\\\cdots 𝑊_4^{[4]𝑇} \cdots\\\end{aligned}\right]}^{W^{[1]}}*\overbrace{\left[\begin{aligned}x_1\\x_2\\x_3\end{aligned}\right]}^{input}+\overbrace{\left[ \begin{aligned}b_1^{[1]}\\b_2^{[2]}\\b_3^{[3]}\\b_4^{[4]}\\\end{aligned}\right]}^{b^{[1]}} \]

3.4 多样本向量化（Vectorizing across multiple examples）

如何向量化多个训练样本，并计算出结果：

逻辑回归是将各个训练样本组合成矩阵，对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形，让神经网络计算出输出值。这种计算是所有的训练样本同时进行的

想计算𝑚个训练样本上的所有输出，就应该向量化整个计算

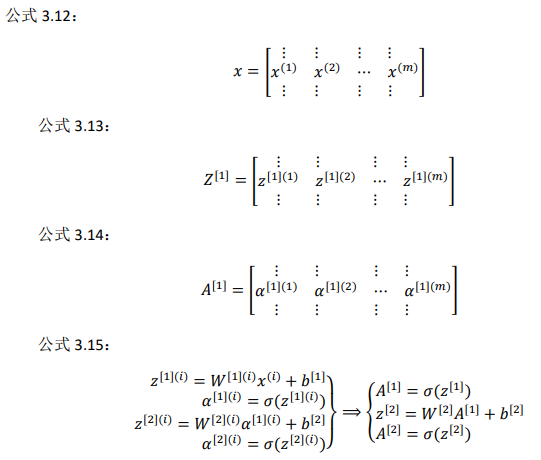
3.5 向 量 化 实 现 的 解 释 （ Justification for vectorized implementation）

为什么上一节中写下的公式就是将多个样本向量 化的正确实现。

\[𝑧^{[1](1)} = 𝑊^{[1]}𝑥^{(1)} + 𝑏^{[1]}\\𝑧^{[1](2)} = 𝑊^{[1]}𝑥^{(2)} + 𝑏^{[1]}\\𝑧^{[1](3)} = 𝑊^{[1]}𝑥^{(3)} + 𝑏^{[1]} \]

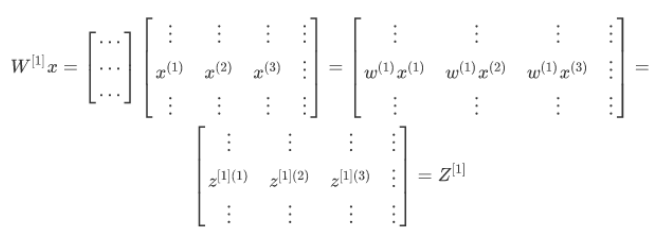
为当有不同的训练样本时，将它们堆到矩阵𝑋的各列中，那么 它们的输出也就会相应的堆叠到矩阵 \(𝑍 ^{[1]}\) 的各列中

类似的分析可以发现，前向传播的其它步也可以使用非常相似的逻辑，即如果将输入 按列向量横向堆叠进矩阵，那么通过公式计算之后，也能得到成列堆叠的输出。

3.6 激活函数（Activation functions）

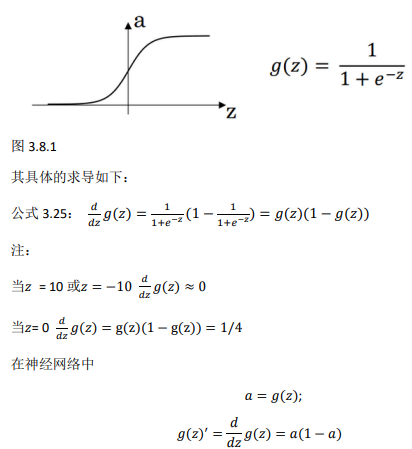
sigmoid 函数：

\(a=\sigma(z)=\frac{1}{1+e^{-z}}\)

更通常的情况下，使用不同的函数\(𝑔(𝑧^{[1]} )\)，𝑔可以是除了 sigmoid 函数意外的非线性函 数。

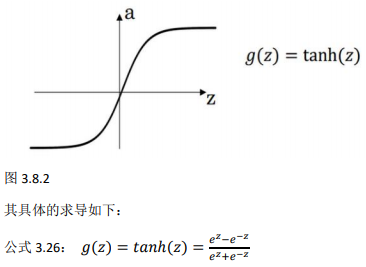
tanh 函数或者双曲正切函数是总体上都优于 sigmoid 函数的激活函数：

\(a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\)

tanh 函数是 sigmoid 的向下平移和伸缩后的结果。对它进行了变形后，穿过了 (0,0)点，并且值域介于+1 和-1 之间。

结果表明，如果在隐藏层上使用函数$𝑡𝑎𝑛ℎ(𝑧^{1} ) $效果总是优于 sigmoid 函数。因为函数值域在-1 和+1 的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用 tanh 函数代替 sigmoid 函数中心化数据，使得数据的平均值更接近 0 而不是 0.5. 这会使下一层学习简单一点

tanh 函数在 所有场合都优于 sigmoid 函数。 但有一个例外：在二分类的问题中，对于输出层，因为𝑦的值是 0 或 1，所以想让𝑦^的数 值介于 0 和 1 之间，而不是在-1 和+1 之间。所以需要使用 sigmoid 激活函数。

\(g(𝑧^{[2]} ) = 𝜎(𝑧^{[2]} )\)

在这个例子里，对隐藏层使用 tanh 激活函数，输出层使用 sigmoid 函数。

sigmoid 函数和 tanh 函数两者共同的缺点是，在𝑧特别大或者特别小的情况下，导数的 梯度或者函数的斜率会变得特别小，最后就会接近于 0，导致降低梯度下降的速度。

另一个很流行的函数是：修正线性单元的函数（ReLu）

𝑎 = 𝑚𝑎𝑥(0, 𝑧)

只要𝑧是正值的情况下，导数恒等于 1，当𝑧是负 值的时候，导数恒等于 0。从实际上来说，当使用𝑧的导数时，𝑧=0 的导数是没有定义的。但 是当编程实现的时候，𝑧的取值刚好等于 0.00000001，这个值相当小，所以，在实践中，不 需要担心这个值，𝑧是等于 0 的时候，假设一个导数是 1 或者 0 效果都可以。

一些选择激活函数的经验法则：

如果输出是 0、1 值（二分类问题），则输出层选择 sigmoid 函数，然后其它的所有单 元都选择 Relu 函数。

另一个版本的 Relu 被称为 Leaky Relu：

当𝑧是负值时，这个函数的值不是等于 0，而是轻微的倾斜：

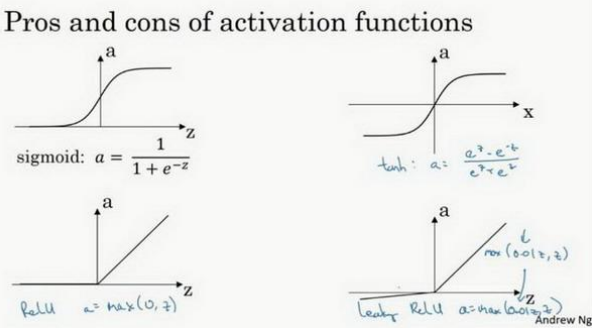
这个函数通常比 Relu 激活函数效果要好，尽管在实际中 Leaky ReLu 使用的并不多。

两者的优点是：

第一，在𝑧的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于 0，在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中， 使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。

第二，sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而 Relu 和 Leaky ReLu 函数大于 0 部分都为常数，不会产生梯度弥散现象。(同时应该注 意到的是，Relu 进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性， 而 Leaky ReLu 不会有这问题)

𝑧在 ReLu 的梯度一半都是 0，但是，有足够的隐藏层使得 z 值大于 0，所以对大多数的 训练数据来说学习过程仍然可以很快。

概括一下：

sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。 tanh 激活函数：tanh 是非常优秀的，几乎适合所有场合。 ReLu 激活函数：最常用的默认函数，，如果不确定用哪个激活函数，就使用 ReLu 或者 Leaky ReLu-- 𝑎 = 𝑚𝑎𝑥(0.01𝑧, 𝑧)

3.7 为什么需要非线性激活函数？（why need a nonlinear activation function?）

事实证明：要让你的神经网络能够计算出有趣的函数，你必须使用非线性激活函数：

如果只用线性激活函数或者叫恒等激励函数，那么神经网络只是把输入线性组合再输出。

事实证明，如果使用线性激活函数或者没有使用一个激活函数，那么无论神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。事实证明如果在隐藏层用线性激活函数，在输出层用 sigmoid 函数，那么这个模型的复杂度和没有任何隐藏层的标准 Logistic 回归是一样的

只有一个地方可以使用线性激活函数------𝑔(𝑧) = 𝑧，就是在做机器学习中的回归问题：

𝑦 是一个实 数，举个例子，比如你想预测房地产价格，𝑦 就不是二分类任务 0 或 1，而是一个实数，从 0 到正无穷。如果𝑦 是个实数，那么在输出层用线性激活函数也许可行，你的输出也是一个 实数，从负无穷到正无穷。

唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，也有一些特殊情况，比如与压缩有关的，在这里不深入讨论。总之在隐层使用线性激活函数非常少见。

3.8 激活函数的导数（Derivatives of activation functions）

1、sigmoid activation function：

2、Tanh activation function：

3、Rectified Linear Unit (ReLU)：

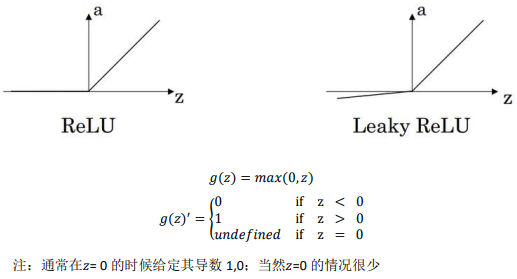
4、Leaky linear unit (Leaky ReLU)

3.9 神 经 网 络 的 梯 度 下 降 （ Gradient descent for neural networks）

以二分类任务为例：

Cost function: 公式：$ 𝐽(𝑊^{1} , 𝑏^{1} , 𝑊^{[2]} , 𝑏^{[2]}) = \frac{1}{𝑚}\sum_{i=1}^mL(\hat{y} , 𝑦)$

loss function 和之前做 logistic 回归完全一样:\(L(a,y)=-( ylog(a)+(1-y)log(1-a) )\)

训练参数需要做梯度下降，在训练神经网络的时候，随机初始化参数很重要，而不是初 始化成全零。当你参数初始化成某些值后，每次梯度下降都会循环计算以下预测值：

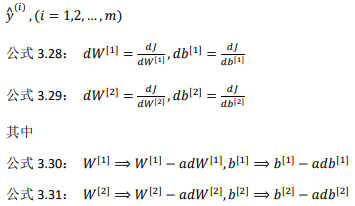
正向传播：

反向传播：

𝑌是1 × 𝑚的矩阵； 这里 np.sum 是 python 的 numpy 命令，axis=1 表示水平相加求和，keepdims 是防止 python 输出那些古怪的秩数(𝑛, )，加上这个确保阵矩阵𝑑𝑏 [2]这个向量输出的维度为(𝑛, 1)这 样标准的形式。

对求导有迷惑的可以参照logistic回归的求导

3.10（选修）直观理解反向传播（Backpropagation intuition）

逻辑回归的推导：

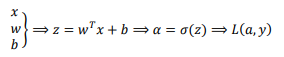
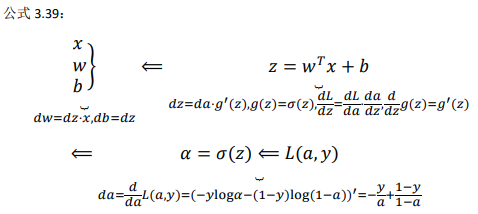
神经网络的计算中，与逻辑回归十分类似，但中间会有多层的计算：

前向传播： 计算\(𝑧^{[1]}\)，\(𝑎^{ [1]}\)，再计算\(𝑧^{ [2]}\)，\(𝑎^{ [2]}\)，最后得到 loss function。 反向传播： 向后推算出\(𝑑𝑎^{[2]}\)，然后推算出\(𝑑𝑧^{[2]}\)，接着推算出\(𝑑𝑎^{[1]}\)，然后推算出\(𝑑𝑧^{[1]}\)。

向后推算出\(𝑑𝑎^{[2]}\)，然后推算出\(𝑑𝑧^{[2]}\)的步骤 可以合为一步：

3.11 随机初始化（Random+Initialization）

对于一个神经网络，如果把权重或者参数都初始化为 0，那么梯度下降将不会起作用：

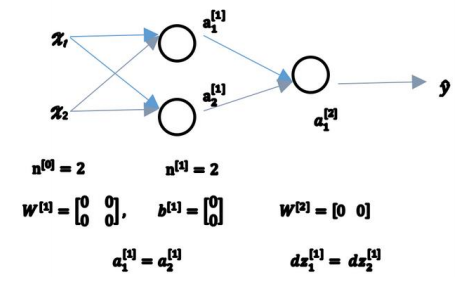
如果这样初始化这个神经网络，那么这两个隐含单元就会完全一样， 因此他们完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代， 这两个隐含单元仍然是同一个函数。

如果把权重都初始化为 0，那么由于隐含单元开始计算同一个函数， 所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同 的，即隐含单元仍是对称的。通过推导，两次、三次、无论多少次迭代，不管训练网络多 长时间，隐含单元仍然计算的是同样的函数。

要想两个不同的隐含单元计算不同的函数， 解决方法就是随机初始化参数：

把 \(𝑊^{[1]}\) 设 为 np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如 0.01，这样把它初始化为很小的随机数。然后𝑏没有这个对称的问题（叫做 symmetry breaking problem），所 以可以把 𝑏 初始化为 0，因为只要随机初始化𝑊你就有不同的隐含单元计算不同的东西， 因此不会有 symmetry breaking 问题了：

0.01：

通常倾向于初始化为很小的随机数。因为如果用 tanh 或者 sigmoid 激活函数，或者说只在输出层有一个 Sigmoid，如果（数值）波动太大，当计算激活值时\(𝑧^{[1]} = 𝑊^{[1]}𝑥 + 𝑏^{[1]}, 𝑎^{[1]} = 𝜎(𝑧^{[1]} ) = 𝑔^{[1]} (𝑧^{[1]})\)如果𝑊很大，𝑧就会很大。𝑧的一些值𝑎就会很大或者很小，因此这种情况下很可能停在 tanh/sigmoid 函数的平坦的地方，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

事实上有时有比 0.01 更好的常数，当训练一个只有一层隐藏层的网络时（这是相对浅的神经网络，没有太多的隐藏层），设为 0.01 可能也可以。但当训练一个非常非常深的神经网络，可能会选择一个不同于的常数而不是 0.01。