吴恩达《深度学习》-课后测验-第一门课 (Neural Networks and Deep Learning)-Week 2 - Neural Network Basics(第二周测验 - 神经网络基础)
Week 2 Quiz - Neural Network Basics(第二周测验 - 神经网络基础)
1. What does a neuron compute?(神经元节点计算什么?)
【 】 A neuron computes an activation function followed by a linear function (z = Wx + b)(神经 元节点先计算激活函数,再计算线性函数(z = Wx + b))
【 】 A neuron computes a linear function (z = Wx + b) followed by an activation function(神经 元节点先计算线性函数(z = Wx + b),再计算激活。)
【 】 A neuron computes a function g that scales the input x linearly (Wx + b)(神经元节点计算 函数 g,函数 g 计算(Wx + b))
【 】 A neuron computes the mean of all features before applying the output to an activation function(在 将输出应用于激活函数之前,神经元节点计算所有特征的平均值)
答案
【【★】 A neuron computes a linear function (z = Wx + b) followed by an activation function(神经 元节点先计算线性函数(z = Wx + b),再计算激活。)
Note: The output of a neuron is a = g(Wx + b) where g is the activation function (sigmoid, tanh, ReLU, …).(注:神经元的输出是 a = g(Wx + b),其中 g 是激活函数(sigmoid,tanh, ReLU,…))
\2. Which of these is the “Logistic Loss”?(下面哪一个是 Logistic 损失?)
【 】损失函数:\(L(\hat{y}^{(i)},y^{(i)})=-y^{(i)}log\hat{y}^{(i)}-(1-y^{(i)})log(1-\hat{y}^{(i)})\)
Note: We are using a cross-entropy loss function.(注:我们使用交叉熵损失函数。)
\3. Suppose img is a (32,32,3) array, representing a 32x32 image with 3 color channels red, green and blue. How do you reshape this into a column vector?(假设 img 是一个(32,32,3) 数组,具有 3 个颜色通道:红色、绿色和蓝色的 32x32 像素的图像。 如何将其重新转换为 列向量?)
答案
x = img.reshape((32 * 32 * 3, 1))
\4. Consider the two following random arrays “a” and “b”:(看一下下面的这两个随机数组“a”和 “b”:)
a = np.random.randn(2, 3) # a.shape = (2, 3)
b = np.random.randn(2, 1) # b.shape = (2, 1)
c = a + b
What will be the shape of “c”?(请问数组 c 的维度是多少?)
答案
c.shape = (2, 3)
b (column vector) is copied 3 times so that it can be summed to each column of a. Therefore, c.shape = (2, 3).( B(列向量)复制 3 次,以便它可以和 A 的每一列相加,所 以:c.shape = (2, 3))
\5. Consider the two following random arrays “a” and “b”:(看一下下面的这两个随机数组“a”和 “b”)
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b
What will be the shape of “c”?(请问数组“c”的维度是多少?)
答案
The computation cannot happen because the sizes don’t match. It’s going to be “error”! Note:“*” operator indicates element-wise multiplication. Element-wise multiplication requires same dimension between two matrices. It’s going to be an error.(注:运算符 “*” 说明了按元素乘法来相 乘,但是元素乘法需要两个矩阵之间的维数相同,所以这将报错,无法计算。)
\6. Suppose you have 𝒏𝒙 input features per example. Recall that \(𝑿 = [𝒙^{(𝟏)} , 𝒙^{(𝟐)} … 𝒙^{(𝒎)} ]\). What is the dimension of X?(假设你的每一个样本有𝒏𝒙个输入特征,想一下在\(𝑿 = [𝒙^{(𝟏)} , 𝒙^{(𝟐)} … 𝒙^{(𝒎)} ]\)中,X 的维度是多少?)
答案
(𝑛𝑥, 𝑚)

\7. Recall that np.dot(a,b) performs a matrix multiplication on a and b, whereas a*b performs an element-wise multiplication.(回想一下,np.dot(a,b)在 a 和 b 上执行矩阵乘法,而“a * b”执行元素方式的乘法。)Consider the two following random arrays “a” and “b”:(看一下下 面的这两个随机数组“a”和“b”:)
a = np.random.randn(12288, 150) # a.shape = (12288, 150)
b = np.random.randn(150, 45) # b.shape = (150, 45)
c = np.dot(a, b)
What is the shape of c?(请问 c 的维度是多少?)
答案
c.shape = (12288, 45), this is a simple matrix multiplication example.( c.shape = (12288, 45), 这 是一个简单的矩阵乘法例子。)
\8. Consider the following code snippet:(看一下下面的这个代码片段:)
# a.shape = (3,4)
# b.shape = (4,1)
for i in range(3):
for j in range(4):
c[i][j] = a[i][j] + b[j]
How do you vectorize this?(请问要怎么把它们向量化?)
答案
c = a + b.T
\9. Consider the following code:(看一下下面的代码:)
a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b
What will be c?(请问 c 的维度会是多少? )
答案
c.shape = (3, 3)
This will invoke broadcasting, so b is copied three times to become (3,3), and * is an elementwise product so c.shape = (3, 3).(这将会使用广播机制,b 会被复制三次,就会变成 (3,3),再使用元素乘法。所以: c.shape = (3, 3).)
\10. Consider the following computation graph,What is the output J.(看一下下面的计算图,J 输 出是什么:)
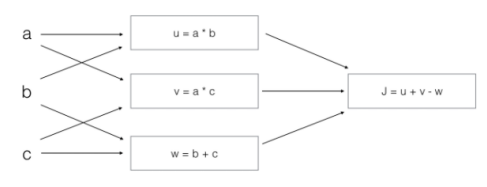
答案
J = u + v - w
= a * b + a * c - (b + c)
= a * (b + c) - (b + c)
= (a - 1) * (b + c)
Week 2 Code Assignments:
✧Course 1 - 神经网络和深度学习 - 第二周作业 - 具有神经网络思维的Logistic回归
✦assignment2_1:Python Basics with Numpy (optional assignment)
https://github.com/phoenixash520/CS230-Code-assignments


 浙公网安备 33010602011771号
浙公网安备 33010602011771号