吴恩达《深度学习》-第一门课 (Neural Networks and Deep Learning)-第二周：(Basics of Neural Network programming)-课程笔记

第二周：神经网络的编程基础 (Basics of Neural Network programming)

2.1、二分类(Binary Classification)

二分类问题的目标就是习得一个分类器，它以图片的特征向量（RGB值的矩阵，最后延展成一维矩阵x，如下）作为输入，然后预测输出结果𝑦为 1 还是 0：

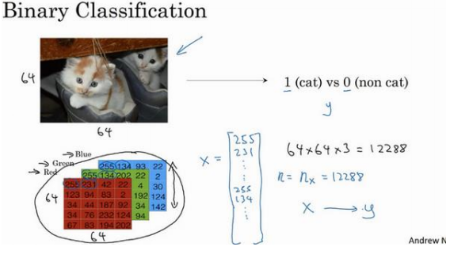
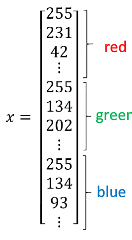
主要需要注意的是一些符号定义：

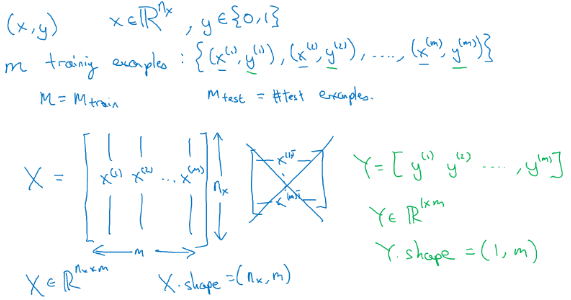
𝑥：表示一个𝑛𝑥维数据，为输入数据，维度为(𝑛𝑥, 1)；

𝑦：表示输出结果，取值为(0,1)；

(𝑥 (𝑖) , 𝑦 (𝑖) )：表示第𝑖组数据，可能是训练数据，也可能是测试数据，此处默认为训练数 据；

𝑋 = [𝑥 (1) , 𝑥 (2) , . . . , 𝑥 (𝑚) ]：表示所有的训练数据集的输入值，放在一个 𝑛𝑥 × 𝑚的矩阵中， 其中𝑚表示样本数目，输入神经网络时数据形状为 $ nx∗m:([x(1),x(2)⋯ x(m)]) $ 而非 \(m * nx:\left(\begin{matrix} x_{(1)}^T \\ x_{(2)}^T \\ \vdots\\ x_{(m)}^T \\ \end{matrix}\right)\)

𝑌 = [𝑦 (1) , 𝑦 (2) , . . . , 𝑦 (𝑚) ]：对应表示所有训练数据集的输出值，维度为1 × 𝑚。

python实现的时候：𝑋.shape 等于(𝑛𝑥, 𝑚)，Y.shape 等于(1, 𝑚)

---

2.2、 逻辑回归(Logistic Regression)

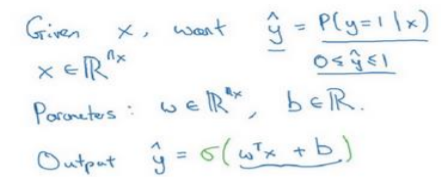
让\(\hat{y}\)表示实际值𝑦等于 1 的机率的话， \(\hat{y}\)应该在 0 到 1 之间。因为\(w^Tx +b\)可能比 1 要大得多，或者甚至为一个负值。因此在逻辑回归中，输出应该是\(\hat{y}\)等于由上面得到的线性函数式子\(w^Tx +b\)作为自变量的 sigmoid 函数中，将线性函数转换为非线性函数。

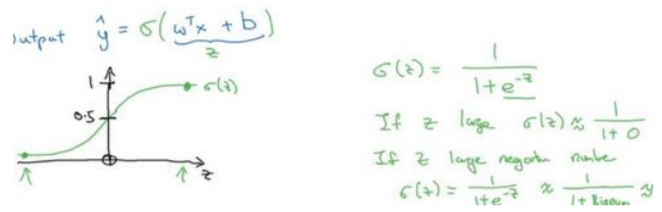
介绍一种符号惯例，可以让参数𝑤和参数𝑏分开 :

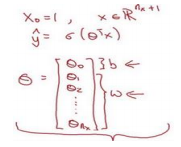
定义一个额外的特征称之为\(x_0\)，并且使它等于 1，那么现在𝑋就是一 个𝑛𝑥+1 维的变量

这样\(\theta_0\)就充当了𝑏，这是一个实数，而剩下的\(\theta_1\) 直到\(\theta_{nx}\) 充当了\(w\)

---

2.3 逻辑回归的代价函数（Logistic Regression Cost Function）

训练代价函数来得到参数𝑤和参数b：

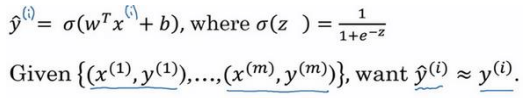
损失函数又叫做误差函数，Loss function：\(L(\hat{y},y)\).

逻辑回归中用到的损失函数是： \(L(\hat{y},y)=-(ylog(\hat{y}+(1-y)log(1-\hat{y}))\)

使用该Loss function 的理由：

​ 当𝑦 = 1时损失函数\(𝐿 = −log(\hat{y})\)，如果想要损失函数𝐿尽可能得小，那么 \(\hat{y}\) 就要尽可能大， 因为 sigmoid 函数取值[0,1]，所以 \(\hat{y}\) 会无限接近于 1。

​ 当𝑦 = 0时损失函数𝐿 = −log(1 − \(\hat{y}\) )，如果想要损失函数𝐿尽可能得小，那么\(\hat{y}\) 就要尽可能小，因为 sigmoid 函数取值[0,1]，所以\(\hat{y}\) 会无限接近于 0。

有很多的函数效果和现在这个类似，就是如果𝑦等于 1，我们就尽可能让 \(\hat{y}\) 变大，如果𝑦等于 0，我们就尽可能让 \(\hat{y}\) 变小。

损失函数是在单个训练样本中定义，它衡量的是算法在单个训练样本中表现。

衡量算法在全部训练样本上的表现，需要定义一个算法的代价函数（Cost function）：对𝑚个样本的损失函数求和然后除以𝑚：

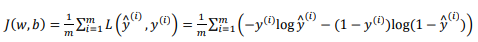
在训练逻辑回归模型时候，需要找到合适的𝑤和𝑏，来让代价函数 𝐽 的总代价降到最低。

逻辑回归可以看做是一个非常小的神经网络。

---

2.4 梯度下降法（Gradient Descent）

梯度下降法（仅有一个参数）

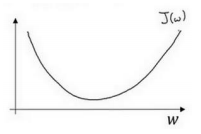
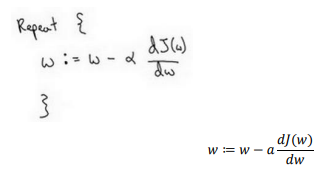
=表示更新参数.

𝑎 表示学习率（learning rate），用来控制步长（step）.

\(\frac{𝑑𝐽(𝑤)}{𝑑𝑤}\)就 是函数𝐽(𝑤)对𝑤 求导（derivative） 对于导数更加形象化的理解就是斜率（slope）.

逻辑回归的代价函数（成本函数）𝐽(𝑤, 𝑏)是含有两个参数的：

\[w := w - a\frac{\partial J(w,b)}{\partial w} \qquad b := b - a\frac{\partial J(w,b)}{\partial b} \]

在代码中使用 𝑑𝑤 表示 \(\frac{\partial J(w,b)}{\partial w}\)， 使用 \(db\) 表示\(\frac{\partial J(w,b)}{\partial b}\)

---

2.5 导数（Derivatives）

超简单导数讲解，没什么笔记。

---

2.6 更多的导数例子（More Derivative Examples）

一些基础函数的导数讲解。

---

2.7 计算图（Computation Graph）

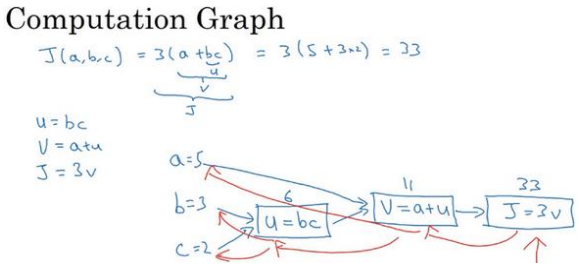
神经网络的计算，都是按照前向或反向传播过程组织的：

首先我们计算出一个新的网络的输出（前向过程），紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。

计算图解释了为什么我们用这种方式组织这些计算过程，计算图组织计算的形式是用蓝色箭头从左到右的计算。

---

2.8 使用计算图求导数（Derivatives with a Computation Graph）

主要使用的是求导中的链式法则：

\[\frac{dJ}{du} = \frac{dJ}{dv} \frac{dv}{du} \quad , \quad\frac{dJ}{db}=\frac{dJ}{du}\frac{du}{db} \quad , \quad\frac{dJ}{da}=\frac{dJ}{du}\frac{du}{da} \]

这是一个计算流程图，就是正向或者说从左到右的计算来计算成本函数𝐽，然后反向从右到左计算导数。

---

2.9 逻辑回归中的梯度下降（Logistic Regression Gradient Descent）

𝑤和𝑏的修正量,\(a\)为学习率:

\[w:=w-a\frac{\partial J(w,b)}{\partial w}\quad,\quad b:=b-a\frac{\partial J(w,b)}{\partial b} \]

微积分得到：

\[\frac{dL(a,y)}{da}=-(y/a+(1-y)/(1-a)) \]

\[\frac{da}{dz}=f'(z)=\left( \frac{1}{1+e^{-z}}\right)'=\frac{e^{-z}}{(1+e^{-z})^2}=\frac{1+e^{-z}-1}{(1+e^{-z})^2}=\frac{1}{(1+e^{-z})}\left(1-\frac{1}{1+e^{-z}}\right)=a(1-a) \]

\[\frac{dL(a,y)}{dz}=\frac{dL}{dz}=(\frac{dL}{da})\cdot(\frac{da}{dz})=(-\frac{y}{a}+\frac{(1-y)}{(1-a)})\cdot a(1-a)=a-y​ \]

现在进行最后一步反向推导：

\(dw_1\)表示\(\frac{\partial L}{\partial w_1}\)，\(dw_2\)表示\(\frac{\partial L}{\partial w_2}\)，\(db=dz\)。

然后: 更新\(𝑤_1 = 𝑤_1 − 𝑎𝑑𝑤_1\)， 更新\(𝑤_2 = 𝑤_2 − 𝑎𝑑𝑤_2\)， 更新\(𝑏 = 𝑏 − 𝛼𝑑𝑏\)。

2.10 m 个样本的梯度下降(Gradient Descent on m Examples)

损失函数𝐽(𝑤, 𝑏)的定义：

\[J(w,b)=\frac{1}{m}\sum_{i=1}^mL(a^{(i)},y^{(i)}) \]

现在带有求和的全局代价函数，实际上是 1 到𝑚项各个损失的平均。 它表明全局代价函数对𝑤1的微分，对𝑤1的微分也同样是各项损失对𝑤1微分的平均。

代码流程：

初始化：J=0;dw1=0;dw2=0;db=0;
 for i = 1 to m 
	z(i) = wx(i)+b; 
	a(i) = sigmoid(z(i)); 
	J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i)); 
	dz(i) = a(i)-y(i); 
	dw1 += x1(i)dz(i); 
	dw2 += x2(i)dz(i); 
	db += dz(i); J/= m; 
	dw1/= m; 
	dw2/= m; 
	db/= m;
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db

这种计算中有两个缺点：

需要编写两个 for 循环。 第一个 for 循环是一个小循环遍历𝑚个训练样本，第二个 for 循环是一个遍历所有特征的 for 循环。这个例子中只有 2 个特征，所以𝑛等于 2 并且𝑛𝑥 等于 2。 但如果有更多特征， 需要一 个 for 循环遍历所有𝑛个特征。

向量化技术：可以允 许代码摆脱这些显式的 for 循环。

2.11 向量化(Vectorization)

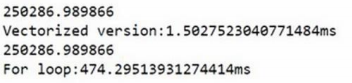
矩阵向量的加减，主要突出：采用numpy库函数进行向量的运算速度比使用for循环快超级多！

import numpy as np #导入 numpy 库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过 round 随机得到两个一百万维度的数组
c = np.dot(a,b)#向量相加

for i in range(1000000):#采用for循环
 c += a[i]*b[i]

运行时间对比：

2.12 向量化的更多例子（More Examples of Vectorization）

矩阵乘法$ u=Av $:

向量化方式就可以用𝑢 = 𝑛𝑝. 𝑑𝑜𝑡(𝐴, 𝑣)，消除了两层循环使得代码运行速度更快。

主要就是用numpy进行矩阵的运算。

2.13 向量化逻辑回归(Vectorizing Logistic Regression)

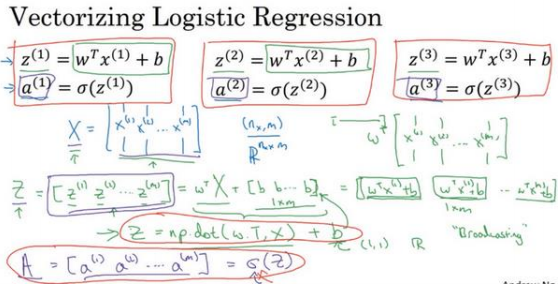
用numpy库的计算表示logistic regression。

2.14 向量化 logistic 回归的梯度输出（Vectorizing Logistic Regression's Gradient）

2.13中虽然去掉了一个for循环：针对w、d等参数的，但仍有一个遍历训练集的循环：

\[𝑑𝑤 = 0\\ 𝑑𝑤 += 𝑥^{(1)}∗ 𝑑𝑧^{(1)}\\ 𝑑𝑤 += 𝑥^{(2)}∗ 𝑑𝑧^{(2)}\\ ………….\\ \\ 𝑑𝑤 += 𝑥^{(𝑚)}∗ 𝑑𝑧(𝑚)\\ 𝑑𝑤 = \frac{𝑑𝑤}{𝑚}\\ 𝑑𝑏 = 0\\ 𝑑𝑏 += 𝑑𝑧^{(1)}\\ 𝑑𝑏 += 𝑑𝑧^{(2)}\\ ………….\\ 𝑑𝑏 += 𝑑𝑧^{(𝑚)}\\ 𝑑𝑏 = \frac{𝑑𝑏}{𝑚}\\ \]

但计算 𝑑𝑤 仍然需要一个循环遍历训练集，所以就用一个np.sum函数来快速替代就好了。

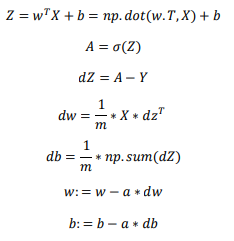
2.15 Python 中的广播（Broadcasting in Python）

broadcasting可以这样理解：如果你有一个mn的矩阵，让它加减乘除一个1n的矩阵，它会被复制m次，成为一个mn的矩阵，然后再逐元素地进行加减乘除操作。同样地对m1的矩阵成立：

2.16 关于 python _ numpy 向量的说明（A note on python or numpy vectors）

Python 语言巨大的灵活性也是缺点，由于广播巨大的灵活性，有时候可能会产生很细微或者看起来很奇怪的 bug。例如，将一个列向量添加到一个行向量中，会以为它报出维度不匹配或类型错误之类的错误，但是实际上会得到一个行向量和列向量的求和。

是如果对 Python 不熟悉的话，就可能会非常生硬、非常艰难地去寻找 bug。

置𝑎 = 𝑛𝑝. 𝑟𝑎𝑛𝑑𝑜𝑚. 𝑟𝑎𝑛𝑑𝑛(5)此时 𝑎 的 shape（形 状）是一个(5, )的结构。这在 Python 中被称作一个一维数组。相反，如果你设置 𝑎 为(5,1)，那么这就将置于 5 行 1 列向量中。

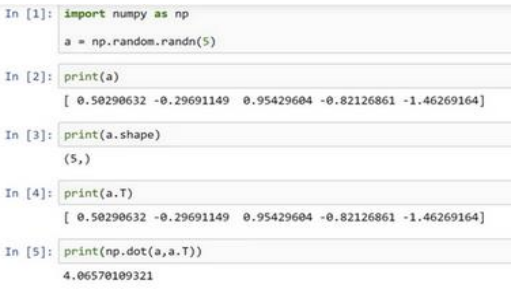
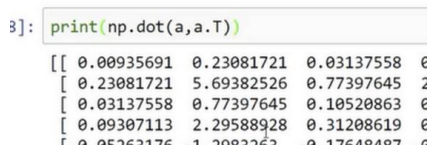
要去简化你的代码，而且不要使用一维数组。总是使用 𝑛 × 1 维矩阵（基本上是列向量），或者 1 × 𝑛 维矩阵（基本上是行向量）

2.17 Jupyter/iPython Notebooks 快速入门（Quick tour of Jupyter/iPython Notebooks）

jupyter介绍，没什么好说的。

2.18 （选修）logistic 损失函数的解释（Explanation of logistic regression cost function）

约定 \(\hat{𝑦} = 𝑝(𝑦 = 1|𝑥)\) ，即算法的输出\(\hat{𝑦}\)是 给定训练样本 𝑥 条件下 𝑦 等于 1 的概率。 换句话说，如果𝑦 = 1，在给定训练样本 𝑥 条件下y = \(\hat{𝑦}\)； 反过来说，如果𝑦 = 0，在给定训练样本𝑥条件下 (𝑦 = 1 − \(\hat{𝑦}\))， 因此，如果 \(\hat{𝑦}\) 代表 𝑦 = 1 的概率，那么1 − \(\hat{𝑦}\)就是 𝑦 = 0的概率。 接下来，我们就来分析这两个条件概率公式。

\[If \qquad y=1:\qquad p(y|x)=\hat{y}\\ If \qquad y=0:\qquad p(y|x)=1-\hat{y} \]

可以将这两个公式合并成一个公式。需要指出的是我们讨论的是二分类问题的损失函 数，因此，𝑦的取值只能是 0 或者 1:

\[p(y|x)=\hat{y}^y(1-\hat{y})^{(1-y)} \]

第一种情况:\(y=1 \quad 𝑝(𝑦|𝑥) = \hat{y}\)

第二种情况:$y=0\quad p(y|x)=1\times(1-\hat{y})^{1-y} $

由于 log 函数是严格单调递增的函数，最大化 𝑙𝑜𝑔(𝑝(𝑦|𝑥)) 等价于最大化 𝑝(𝑦|𝑥) 通过对数 函数化简为：

\[ylog(\hat{y})+(1-y)log(1-\hat{y}) \]