龙格-库塔方法

龙格-库塔方法

使用四阶龙格-库塔方法求解下述微分方程：

\[y'=\frac{2}{3}xy^{-2}\\ y(0)=1 \]

import numpy as np


def RK(x0, y0, h, n, func):
    """
    4阶龙格-库塔方法
    :param x0: 初始点x坐标
    :param y0: 初始点y坐标
    :param h: 步长
    :param n: 迭代次数
    :param func: 事先定义好的f(x,y)
    :return:
    """
    x = np.linspace(x0, x0 + (n - 1) * h, num=n)
    y = np.zeros_like(x)
    y[0] = y0
    for i in range(n - 1):
        k1 = func(x[i], y[i])
        k2 = func(x[i] + h / 2, y[i] + h * k1 / 2)
        k3 = func(x[i] + h / 2, y[i] + h * k2 / 2)
        k4 = func(x[i] + h, y[i] + h * k3)
        y[i + 1] = y[i] + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6
    return x, y


if __name__ == '__main__':
    # y'=f(x,y)=2x/(3y^2)
    f = lambda x, y: 2 * x / (3 * y * y)
    X, Y = RK(0, 1, h=0.4, n=5, func=f)
    # 测试结果
    # X = [0.  0.4 0.8 1.2 1.6]
    # Y = [1.         1.05075062 1.17933176 1.34631543 1.52696316]
    print("X=", X)
    print("Y=", Y)

一阶方程组

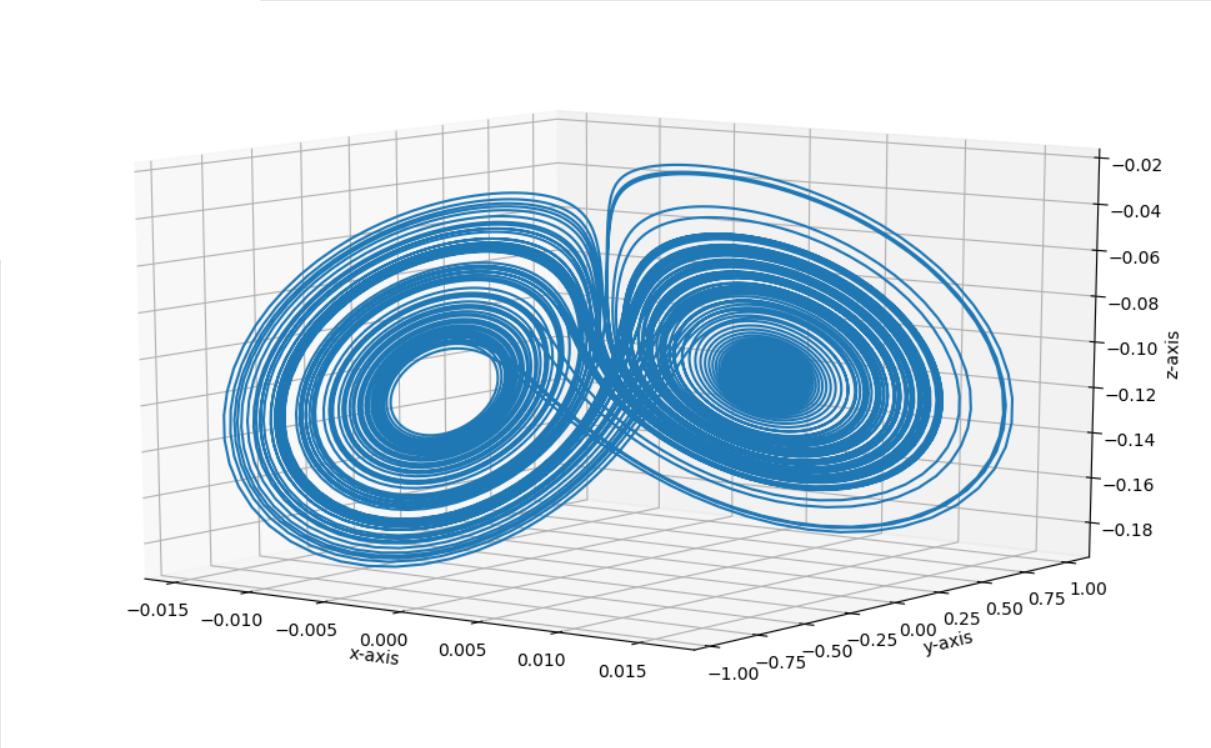
求解洛伦兹型系统：

\[\left\{\begin{aligned} &x'=-\sigma x+\tau y+ \epsilon yz\\ &y'=rx-qy+sxz\\ &z'=-bz+\mu xy \end{aligned}\right. \]

其中\(x,y,z\)均是关于时间\(t\)的函数。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def RK4(x0, y0, h, n, fs):
    m = len(fs)
    x = np.linspace(x0, x0 + (n - 1) * h, num=n)
    y = np.zeros(shape=(m, n))
    y[:, 0] = y0
    for i in range(n - 1):
        # 计算K1
        K1 = np.zeros(m)
        for index, f in enumerate(fs):
            K1[index] = f(x[i], y[:, i])
        # 计算K2
        K2 = np.zeros(m)
        for index, f in enumerate(fs):
            K2[index] = f(x[i] + h / 2, y[:, i] + h * K1 / 2)
        # 计算K3
        K3 = np.zeros(m)
        for index, f in enumerate(fs):
            K3[index] = f(x[i] + h / 2, y[:, i] + h * K2 / 2)
        # 计算k4
        K4 = np.zeros(m)
        for index, f in enumerate(fs):
            K4[index] = f(x[i] + h, y[:, i] + h * K3)

        y[:, i + 1] = y[:, i] + h * (K1 + 2 * K2 + 2 * K3 + K4) / 6
    return x, y


if __name__ == '__main__':
    # 求解洛伦兹型系统
    sigma, tau, epsilon = 0.25, 0.06, 0.5
    r, q, s = 120, 1.3, 1.5
    b, u = 0.4, -20
    fs = [
        lambda x, y: -sigma * y[0] + tau * y[1] + epsilon * y[1] * y[2],
        lambda x, y: r * y[0] - q * y[1] + s * y[0] * y[2],
        lambda x, y: -b * y[2] + u * y[0] * y[1]
    ]
    x, y = RK4(0, np.array([0.005, 0.4596, -0.1146]), 0.05, 20000, fs)
    # 绘图
    ax = Axes3D(plt.figure())
    ax.plot(y[0], y[1], y[2])
    ax.set_xlabel('x-axis')
    ax.set_ylabel('y-axis')
    ax.set_zlabel('z-axis')
    plt.show()

测试结果：