4 二次剩余
4.1 二次剩余的定义
定义4-1: 设\(p\)是奇素数,\(a\)是整数且\((a,p)=1\)。若\(x^2\equiv a(mod\;p)\)有解,则称\(a\)为模\(p\)的二次剩余。否则称\(a\)为模\(p\)的二次非剩余。
这里并未考虑\(p=2\)的情况,因为任意一个整数均是模2的二次剩余。
定理4-1:模\(p\)的二次剩余和二次非剩余的个数均是\((p-1)/2\)个,且模\(p\)的全部二次剩余为:
\[1^2,2^2,\cdots,(\frac{p-1}{2})^2\mod p
\]
证明:
任意整数模\(p\)的所有可能结果为:\(0,1,2,\cdots,p-1\)。因为\(p|0\),所以考虑二次剩余的时候,不需要将0考虑在内。如果我们将定义放宽一点,我们可以说0是任意一个正整数的二次剩余,这太平凡了,于是今后我们不在将0纳入二次剩余的考虑范围内。
寻找二次剩余最简单直接的方法就是计算:
\[1^2,2^2,\cdots,(\frac{p-1}{2})^2,(\frac{p+1}{2})^2,\cdots,(p-1)^2\mod p
\]
便可以找到所有的二次剩余。
但是经过计算之后,我们可以发现对于\(1\le x \le (p-1)/2,(p+1)/2\le p-x\le p-1\),有以下关系成立:
\[x^2\equiv(p-x)^2\mod p
\]
这意味着\(x^2\)和\((p-x)^2\)实际上指的是同一个二次剩余,于是我们只需要计算\(x^2(mod\;p),1\le x\le (p-1)/2\),便可以找到所有的二次剩余。
此时,我们想知道通过\(x^2(mod\;p)\)计算出来的二次剩余是否两两不同。因此,我们假设存在整数\(a,b\)使得\(a^2\equiv b^2(mod\;p)\),其中\(1\le a,b \le (p-1)/2\)。于是有
\[a^2\equiv b^2(mod\;p)\Rightarrow p|(a+b)(a-b)
\]
因为,\(1<a+b<p\)且\(p\)是素数。所以,\(p|(a-b)\)成立。
又因为\(0\le|a-b|<p\),所以\(a=b\)。
综上可知,定理4-1成立。
4.2 二次剩余的性质
定理4-2:【欧拉判别条件】若\((a,p)=1\),则
-
\(a\)是模\(p\)的二次剩余的充要条件为:
\[a^{\frac{p-1}2}\equiv1\mod p
\]
-
\(a\)是模\(p\)的二次非剩余的充要条件为:
\[a^{\frac{p-1}2}\equiv-1\mod p
\]
证明:
考虑整数\(x\)且\((x,p)=1\),所以根据欧拉定理,可得
\[x^{p-1}\equiv1\mod p\Leftrightarrow x^{\frac{p-1}{2}}\equiv\pm1\mod p
\]
上述式子说明,对于任意给定的一个整数\(x\),下面两个式子有且仅有一个成立:
- \(x^{(p-1)/2}\equiv1(mod\;p)\)
- \(x^{(p-1)/2}\equiv -1(mod\;p)\)
根据定理4-1,模\(p\)的二次剩余一共有\((p-1)/2\)个,所以二次非剩余也有\((p-1)/2\)个。因此,我们的证明思路就是:
- 模\(p\)的所有二次剩余均是\(x^{(p-1)/2}\equiv1(mod\;p)\)的根
- 模\(p\)的所有二次非剩余均是\(x^{(p-1)/2}\equiv-1(mod\;p)\)的根
若\(a\)是模\(p\)的二次剩余,那么存在整数\(x\)使得\(x^2\equiv a(mod\;p)\),因此
\[a^{\frac{p-1}2}\equiv(x^2)^{\frac{p-1}2}\equiv x^{p-1}\equiv1\mod p
\]
对于任意的二次剩余上述式子均成立,这意味着模\(p\)的所有二次剩余都是方程\(x^{(p-1)/2}\equiv1(mod\;p)\)的根。根据定理3-5可知,方程\(x^{(p-1)/2}\equiv1(mod\;p)\)根的个数不超过\((p-1)/2\)个。
因此,模\(p\)的所有二次剩余就是方程\(x^{(p-1)/2}\equiv1(mod\;p)\)所有的根。所以,所有的二次非剩余均是方程\(x^{(p-1)/2}\equiv-1(mod\;p)\)的根。这就证明了定理4-2。
补充说明: 为什么\(x^2\equiv1(mod\;p)\)成立时,一定会有\(x\equiv\pm1(mod\;p)\)成立(反过来显然成立)?
\[\begin{aligned}
1\equiv x^2&\equiv(1+x-1)^2\\
&\equiv 1+2(x-1)+(x-1)^2\\
&\equiv 1+(x+1)(x-1)\mod p
\end{aligned}
\]
因此我们可以得到\(p|(x+1)(x-1)\),考虑\(1\le x\le p-1\)的情况(因为其他的情况,在模\(p\)的意义下是等价的)。只有当\(x=1\)或\(x=p-1\)的时候,才能使得\(p|(x+1)(x-1)\)成立。因此\(x\equiv\pm1(mod\;p)\)成立。
例题: 求模11的所有二次剩余。
选取模11的一个简化剩余系:\(\{\pm1,\pm2,\pm3,\pm4,\pm5\}\)
可以验证:
\[1^{\frac{11-1}{2}}\equiv1\mod11\\
(-2)^{\frac{11-1}{2}}\equiv1\mod11\\
3^{\frac{11-1}{2}}\equiv1\mod11\\
4^{\frac{11-1}{2}}\equiv1\mod11\\
5^{\frac{11-1}{2}}\equiv1\mod11\\
\]
因为模11一共有\((11-1)/2=5\)个二次剩余,因此\(1,-2,3,4,5\)就是所要求的二次剩余。其余的均为模11的二次非剩余。
4.3 勒让德(Legendre)符号
定义4-2: 给定奇素数\(p\),对于整数\(n\),定义勒让德符号为
\[\left(\frac{n}p\right)=
\left\{\begin{aligned}
0,\quad &p|n\\
1,\quad &n\in QR(p)\\
-1,\quad&n\not\in QR(p)
\end{aligned}\right.
\]
其中\(QR(p)\)定义为由模\(p\)二次剩余组成的集合,即\(QR(p)=\{x|x^{(p-1)/2}\equiv1(mod\;p),x\in Z\}\)。
勒让德符号的性质:
(1)若\(n_1\equiv n_2(mod\;p)\),则\(\left(\frac{n_1}p\right)=\left(\frac{n_2}p\right)\)。即\(n_1,n_2\)在同余意义下等价,因此其勒让德符号相等,也可以通过分类讨论证明。
(2)若\(p\nmid n\),则\(\left(\frac{n^2}p\right)=1\),即\(x^2\equiv n^2(mod\;p)\)有解,显然\(x\equiv n(mod\;p)\)就是一个解。
(3)\(\left(\frac{1}p\right)=1\),即\(x^2\equiv1(mod\;p)\)有解,显然\(x\equiv1(mod\;p)\)就是一个解。
(4)同余方程\(x^2\equiv n(mod\;p)\)的解数为\(1+\left(\frac{n}p\right)\)。
对性质(4)进行分类讨论:
- 当\(p|n\)时,原方程变为\(x^2\equiv0(mod\;p)\),此时仅有一个解\(x\equiv0(mod\;p)\)。
- 当\(n\in QR(p)\),若\(x_0\)是原方程的一个解,那么\((p-x_0)^2\equiv x_0^2(mod\;p)\),于是\(p-x_0\)也是原方程的一个解。
- 当\(n\not\in QR(p)\),则此方程无解。
定理4-3 【欧拉判别法】将定理4-2和勒让德符号的定义结合起来,可以得到
\[\left(\frac{n}p\right)\equiv n^{\frac{p-1}2}\mod p
\]
可以验证,当\(p|n\)的时候,上述式子也是成立的。理论上我们就可以通过上述式子判别整数\(n\)是否为模\(p\)的二次剩余。
定理4-4: 若\(m,n\)为整数,则勒让德符号具有以下等式关系
\[\left(\frac{mn}p\right)=\left(\frac{m}p\right)\left(\frac{n}p\right)
\]
证明如下:
\[\left(\frac{mn}p\right)\equiv(mn)^{\frac{p-1}2}
\equiv(m^{\frac{p-1}2})(n^{\frac{p-1}2})\equiv
\left(\frac{m}p\right)\left(\frac{n}p\right)\mod p
\]
对于任意一个整数\(m\),根据算术基本定理,我们可以将其表示为\(m=\pm2^{\alpha_1}q_2^{\alpha_2}\cdots q_k^{\alpha_k}\),其中\(q_2,\cdots,q_k\)都是奇素数。利用定理4-4,我们可以得到
\[\left(\frac{m}p\right)=\left(\frac{\pm1}p\right)
\left(\frac{2}p\right)^{\alpha_1}
\left(\frac{q_2}p\right)^{\alpha_2}\cdots
\left(\frac{q_k}p\right)^{\alpha_k}
\]
于是我们只需要能够计算下列三种情况的勒让德符号,即可计算任意整数的勒让德符号:
\[\left(\frac{-1}p\right),\left(\frac{2}p\right),\left(\frac{q}p\right)
\]
其中\(q\)是奇素数。
根据欧拉判别法,我们马上可以得到以下结论:
\[\left(\frac{-1}p\right)\equiv(-1)^{\frac{p-1}2}\mod p
\]
因为\((-1)^{(p-1)/2}\)本身的计算结果就是\(\pm1\),因此
\[\left(\frac{-1}p\right)=(-1)^{\frac{p-1}2}
\]
推论:当\((p-1)/2\)是偶数的时候,\(-1\in QR(p)\);当\((p-1)/2\)是奇数的时候,\(-1\not\in QR(p)\)。即
\[\left\{\begin{aligned}
p\equiv1(mod\;4),\quad &-1\in QR(p)\\
p\equiv3(mod\;4),\quad&-1\not\in QR(p)
\end{aligned}\right.
\]
为了求解其他两种情况的勒让德符号,下面将引入高斯引理,同时该引理将是我们证明二次互反律的基础。
高斯引理: 设\(p\)是奇素数且\(p\nmid n\),引入整数序列如下
\[n,2n,\cdots,\frac{1}2(p-1)n
\]
将整数序列中每一个数都通过带余除法除以\(p\),得到余数。将这些余数大于\(p/2\)的个数记为\(m\),则
\[\left(\frac{n}{p}\right)=(-1)^m
\]
证明:
将上述整数序列除以\(p\),可以得到\((p-1)/2\)个余数(这些余数均小于\(p\))。
设不超过\(p/2\)的余数共有\(l\)个,分别记为\(a_1,a_2,\cdots,a_l\);设超过\(p/2\)的余数共有\(m\)个,分别记为\(b_1,b_2,\cdots,b_m\)。因此,我们可以得到
\[\begin{aligned}
n\cdot2n\cdots\frac{p-1}{2}n&\equiv n^{\frac{p-1}{2}}\left(\frac{p-1}{2}\right)!\\
&\equiv(a_1a_2\cdots a_l)(b_1b_2\cdots b_m)\\
&\equiv(a_1a_2\cdots a_l)(-1)^m(p-b_1)(p-b_2)\cdots(p-b_m)\mod p
\end{aligned}
\]
此外,我们可以证明这\((p-1)/2\)个余数两两不同。由于上述整数序列可以写成\(kn\)的形式,其中\(1\le k\le(p-1)/2\)。并且这\((p-1)/2\)个余数均不为零,因为\(p\nmid n,p\nmid k\),所以\(p\nmid kn\)。
如果存在某两个余数相同,这意味着存在两个整数\(1\le x,y\le (p-1)/2\),使得
\[xn\equiv yn\mod p
\]
即\(p|(x-y)n\),因为\(p\nmid n\),所以\(p|(x-y)\)。又因为\(0\le|x-y|\le p-1\),因此必然有\(x=y\),即\(a_1,a_2,\cdots,a_l,b_1,b_2,\cdots,b_m\)两两不同。于是\(p-b_1,\cdots,p-b_m\)也两两不同。
接着证明,\(a_i(i=1,\cdots,l)\)与\(p-b_j(j=1,\cdots,m)\)两两不同余。同理,我们假设存在两个整数\(1\le x,y\le (p-1)/2\)使得其同余,那么
\[xn\equiv p-yn\equiv-yn\mod p\Rightarrow p|(x+y)n\Rightarrow p|(x+y)
\]
因为\(1<x+y<p-1\),所以\(p|(x+y)\)不可能成立。因此\(a_i\)与\(p-b_j\)两两不同余。
因为\(p/2<b_1,\cdots,b_m<p\),所以\(0<p-b_1,\cdots,p-b_m<p/2\)。
因为\(0<a_1,\cdots,a_l<p/2\),所以\(0<a_1,\cdots,a_l,p-b_1,\cdots,p-b_m<p/2\)。
从上述证明我们已经知道\(a_i\)与\(p-b_j\)是\((p-1)/2\)个两两不同的整数,并且0到\(p/2\)之间恰好有\((p-1)/2\)个整数。此时,我们将这\((p-1)/2\)个余数从小到大排列,便可以得到
\[1,2,3,\cdots,\frac{p-1}{2}
\]
于是我们有以下结论
\[\begin{aligned}
n\cdot2n\cdots\frac{p-1}{2}n&\equiv n^{\frac{p-1}{2}}\left(\frac{p-1}{2}\right)!\\
&\equiv(a_1a_2\cdots a_l)(-1)^m(p-b_1)(p-b_2)\cdots(p-b_m)\\
&\equiv(-1)^m\cdot1\cdot2\cdots\left(\frac{p-1}{2}\right)\\
&\equiv(-1)^m\left(\frac{p-1}{2}\right)!\mod p
\end{aligned}
\]
因此,根据欧拉判别法我们可以得到
\[\left(\frac{n}{p}\right)\equiv n^{\frac{p-1}{2}}\equiv(-1)^m\mod p
\]
即高斯引理得证。
定理4-5: 若\(p\)为奇素数,那么
\[\left(\frac{2}{p}\right)=(-1)^{\frac{1}{8}(p^2-1)}
\]
证明:
利用高斯引理,构造整数序列
\[2,2\cdot2,\cdots,2\cdot\frac{p-1}{2}
\]
可以发现上述序列可以写为:\(2k(1\le k\le (p-1)/2)\)的形式,且\(1<2k<p\)。如果\(2k\)大于\(p/2\),那么
\[\frac{p}{2}<2k<p\Rightarrow\frac{p}{4}<k<\frac{p}2
\]
因此,\(m\)等于位于\(p/4\)到\(p/2\)之间整数的个数,即
\[m=\left[\frac{p}2\right]-\left[\frac{p}4\right]
\]
其中\([\cdot]\)表示向下取整。
将奇素数\(p\)表示成2进制的形式(奇数的二进制形式最后一位一定为1),则有\(p=(x_n\cdots x_2x_11)_2\),于是\(m\)可以表示为
\[m=(x_n\cdots x_2x_1)_2-(x_n\cdots x_2)_2
\]
由于\(p\equiv(x_2x_11)_2(mod\;8)\),可以将上述两种情况分别写成以下形式:
-
\(x_1=x_2\)等价于\(p\equiv\pm1(mod\;8)\),于是\(p=8k\pm1\),因此
\[\frac{1}8(p^2-1)\equiv8k^2\pm2k\equiv0\mod2
\]
-
\(x_1\ne x_2\)等价于\(p\equiv\pm3(mod\;8)\),于是\(p=8k\pm3\),因此
\[\frac{1}8(p^2-1)\equiv8k^2\pm6k+1\equiv1\mod2
\]
由上述讨论可知,\(m\equiv\frac{1}8(p^2-1)(mod\;2)\),即具有相同奇偶性。因此
\[\left(\frac{2}{p}\right)=(-1)^m=(-1)^{\frac{1}{8}(p^2-1)}
\]
定理4-6: 【二次互反律】设\(p,q\)是奇素数且\(p\ne q\),则
\[\left(\frac{p}{q}\right)=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\left(\frac{q}{p}\right)
\]
证明:
根据高斯引理,构造整数序列
\[p,2p,\cdots,\frac{q-1}2p
\]
设\(a_i(1\le i\le l)\)表示模\(q\)中小于\(q/2\)的所有最小正余数,\(b_j(1\le j\le m)\)表示大于\(q/2\)的所有最小正余数,则
\[\left(\frac{p}{q}\right)=(-1)^m
\]
根据带余除法,可以将序列中的每一个数写成如下形式:
\[pk=\left[\frac{pk}{q}\right]q+r_k,\;1\le k\le\frac{q-1}2
\]
于是有
\[\begin{aligned}
p\frac{q^2-1}8&=p\cdot1+p\cdot2+\cdots+p\cdot\frac{q-1}{2}\\
&=\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]q+\sum_{i=1}^la_i+\sum_{j=1}^mb_j\\
&=\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]q+\sum_{i=1}^la_i+\sum_{j=1}^m(b_j-q)+mq\\
&=\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]q+\sum_{i=1}^la_i+\sum_{j=1}^m(q-b_j)
+2\sum_{j=1}^m(b_j-q)+mq\\
\end{aligned}
\]
根据高斯引理中的证明,我们知道
\[\sum_{i=1}^la_i+\sum_{j=1}^m(q-b_j)=1+2+\cdots+\frac{q-1}{2}=\frac{q^2-1}8
\]
所以
\[\begin{aligned}
p\frac{q^2-1}8&=\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]q+\frac{q^2-1}8
+2\sum_{j=1}^m(b_j-q)+mq
\end{aligned}
\]
因此
\[(p-1)\frac{q^2-1}8=q(m+\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right])
+2\sum_{j=1}^m(b_j-q)
\]
又因为\(2|(p-1),q\equiv1(mod\;2)\),所以上述等式两边模2,则有
\[\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]\equiv-m\mod2
\]
这说明\(m\)与\(\sum_{k=1}^{(q-1)/2}\left[\frac{pk}{q}\right]\)具有相同的奇偶性,于是我们可以得到以下结论
\[\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{m_1}(-1)^{m_2}=(-1)^{m_1+m_2}
\]
其中
\[m_1=\sum_{y=1}^{(q-1)/2}\left[\frac{py}{q}\right]\\
m_2=\sum_{x=1}^{(p-1)/2}\left[\frac{qx}{p}\right]
\]
接下来我们分析\(m_1,m_2\)的奇偶性:
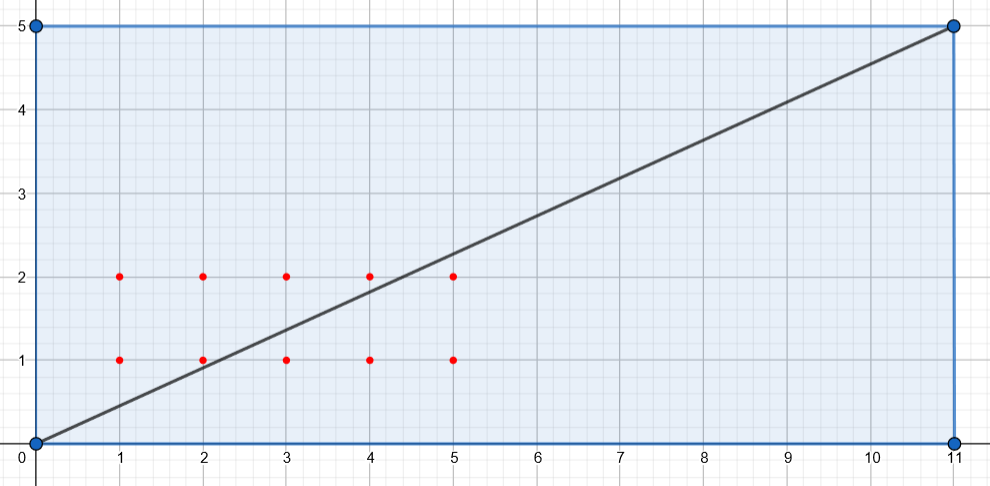
这里不妨假设\(p>q\),考虑\([0,p]\times[0,q]\)矩形内的整点(横纵坐标都是整数)个数,上图是\(p=11,q=5\)的示例。
图中对角线的方程为:
\[y=\frac{q}px
\]
当\(0<x<p\)时,\((x,p)=1,(p,q)=1\)所以\(p\nmid(qx)\),即对角线上没有整点。
\(qx/p\)表示坐标\((x,qx/p)\)到x轴的距离,而\([qx/p]\)数值上就等于,当横坐标为\(x\)时,对角线下方整点的个数(不包括x轴上的整点)。因此\(m_2\)就等于第一象限内且\(1\le x\le(p-1)/2\),对角线下方整点的个数。
\(py/q\)表示坐标\((py/q,y)\)到y轴的距离,而\([py/q]\)数值上就等于,当纵坐标为\(y\)时,对角线上方整点的个数(不包括y轴上的整点)。因此\(m_1\)就等于第一象限内且\(1\le y\le(q-1)/2\),对角线上方整点的个数。
我们很自然会希望\([1,(p-1)/2]\times[1,(q-1)/2]\)矩形区域内的整点个数就是\(m_1+m_2\),但是目前存在一种可能就是存在一些整点位于该矩形区域之外,例如图中的\(y=3\)且位于对角线上方的整点。于是下面我们将说明这种情况不存在:
\[\begin{aligned}
&\frac{q}{p}\cdot\frac{p-1}{2}-\frac{q-1}2=\frac{p-q}{2p}>0\\
&\frac{q}{p}\cdot\frac{p-1}{2}-\frac{q+1}2=\frac{-p-q}{2p}<0
\end{aligned}
\]
所以
\[\frac{q+1}2>\frac{q}{p}\cdot\frac{p-1}{2}>\frac{q-1}2
\Rightarrow\left[\frac{q}{p}\cdot\frac{p-1}{2}\right]=\frac{q-1}2
\]
这说明矩形区域\([1,(p-1)/2]\times[1,(q-1)/2]\)包含了所有可能的整点,所以
\[m_1+m_2=\frac{p-1}{2}\frac{q-1}{2}
\]
所以
\[\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{m_1+m_2}
=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}
\]
因为
\[\left(\frac{q}{p}\right)^2=(\pm1)^2=1
\]
所以上述结果也可以写为
\[\left(\frac{p}{q}\right)=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\left(\frac{q}{p}\right)
\]
4.4 雅可比(Jacobi)符号
定义4-4: 设\(m>1\)是正奇数,可以将其分解为
\[m=\prod_{i=1}^sp_i
\]
其中\(p_i\)是奇素数,且可以重复。
设\(n\)为整数,通过勒让德符号定义雅可比符号:
\[\left(\frac{n}{m}\right)=
\left(\frac{n}{p_1}\right)
\left(\frac{n}{p_2}\right)\cdots\left(\frac{n}{p_s}\right)
\]
通过定义可知,当\(m\)本身就是奇素数的时候,雅可比符号和勒让德符号等价。
雅可比符号的性质:
(1)若\(n_1\equiv n_2(mod\;p)\),则
\[\left(\frac{n_1}m\right)=\left(\frac{n_2}m\right)
\]
(2)若\((m,n)=1\),则
\[\left(\frac{n^2}m\right)=\left(\frac{n}{m^2}\right)=1
\]
(3)若\((m,n)\ne1\),则
\[\left(\frac{n}m\right)=0
\]
(4)
\[\left(\frac{n_1n_2}m\right)
=\left(\frac{n_1}m\right)\left(\frac{n_2}m\right)
\]
(5)
\[\left(\frac{1}m\right)=1
\]
上述性质的证明思路,通过定义将雅可比符号展开成勒让德符号乘积的形式,然后利用勒让德符号的性质即可证明。
定理4-7: 设\(m>1\)为奇数,那么
\[\left(\frac{-1}m\right)=(-1)^{\frac{m-1}{2}}
\]
证明:
首先根据定义展开
\[\left(\frac{-1}{m}\right)=
\left(\frac{-1}{p_1}\right)
\left(\frac{-1}{p_2}\right)\cdots\left(\frac{-1}{p_s}\right)
=(-1)^{E}
\]
其中
\[E=\sum_{i=1}^s\frac{p_i-1}{2}
\]
只需证明\(E\)与\((m-1)/2\)具有相同的奇偶性,即下面式子恒成立
\[\begin{aligned}
&E\equiv\frac{m-1}{2}\mod 2\\
\Leftrightarrow\;&\sum_{i=1}^s\frac{p_i-1}{2}\equiv\frac{1}{2}(\prod_{i=1}^sp_i-1)\mod2\\
\Leftrightarrow\;&\sum_{i=1}^s(p_i-1)\equiv\prod_{i=1}^sp_i-1\mod4
\end{aligned}
\]
奇素数模4只有1,3两种情况(例如奇素数3,5),因为显然奇素数不可能是4的倍数,其次如果奇素数可以写成\(4k+2\)的形式,说明该素数是个偶数,显然不可能。因此,如果\(p_i\)是奇素数,那么
\[p_i\equiv\pm1\mod4
\]
设\(p_1,p_2,\cdots,p_s\)中有\(t\)个数模4余-1,其余模4余1,那么
\[\prod_{i=1}^sp_i-1\equiv(-1)^t-1\mod4\\
\sum_{i=1}^s(p_i-1)\equiv-2t\mod4
\]
分奇偶进行讨论,当\(t=2k,k\in N\)时,
\[\sum_{i=1}^s(p_i-1)\equiv-2t\equiv-4k\equiv0\mod4\\
\prod_{i=1}^sp_i-1\equiv(-1)^t-1\equiv(-1)^{2k}-1\equiv1-1\equiv0\mod4
\]
当\(t=2k+1,k\in N^*\)时
\[\sum_{i=1}^s(p_i-1)\equiv-2t\equiv-2(2k+1)\equiv-4k-2\equiv-2\mod4\\
\prod_{i=1}^sp_i-1\equiv(-1)^t-1\equiv(-1)^{2k+1}-1\equiv-1-1\equiv-2\mod4
\]
综上可知,\(E\)与\((m-1)/2\)具有相同的奇偶性,所以定理4-7成立。
定理4-8: 设\(m>1\)为奇数,那么
\[\left(\frac{2}m\right)=(-1)^{\frac{1}{8}(m^2-1)}
\]
证明:
首先根据定义展开
\[\left(\frac{2}{m}\right)=\left(\frac{2}{p_1}\right)\left(\frac{2}{p_2}\right)\cdots\left(\frac{2}{p_s}\right)=(-1)^{E}
\]
其中
\[E=\frac{1}{8}\sum_{i=1}^s(p_i^2-1)
\]
只需证明\(E\)与\((m^2-1)/8\)具有相同的奇偶性,即下面式子恒成立
\[\begin{aligned}
&E\equiv\frac{m^2-1}{8}\mod 2\\
\Leftrightarrow\;&\frac{1}{8}\sum_{i=1}^s(p_i^2-1)\equiv
\frac{1}{8}(\prod_{i=1}^sp_i^2-1)\mod2\\
\Leftrightarrow\;&\sum_{i=1}^s(p_i^2-1)\equiv\prod_{i=1}^sp_i^2-1\mod16
\end{aligned}
\]
奇素数模4只有1,3两种情况,因此
\[p_i^2\equiv(4k\pm1)^2\equiv16k^2\pm8k+1\equiv1\mod8
\]
于是\(p_i^2\equiv1,9(mod\;16)\),即奇素数模16只有1,9两种可能。
设\(p_1^2,\cdots,p_s^2\)中模16余9的有\(t\)个,其余的数模16余1,那么
\[\sum_{i=1}^s(p_i^2-1)\equiv8t\mod16\\
\prod_{i=1}^sp_i^2-1\equiv9^t-1\mod16
\]
当\(t=2k,k\in N\)时,
\[\sum_{i=1}^s(p_i^2-1)\equiv8t\equiv16k\equiv0\mod16\\
\prod_{i=1}^sp_i^2-1\equiv9^t-1\equiv81^k-1\equiv1-1\equiv0\mod16
\]
当\(t=2k+1,k\in N^*\)时
\[\sum_{i=1}^s(p_i^2-1)\equiv8t\equiv16k+8\equiv8\mod16\\
\prod_{i=1}^sp_i^2-1\equiv9^t-1\equiv81^k\cdot9-1\equiv9-1\equiv8\mod16
\]
综上可知,\(E\)与\((m^2-1)/2\)具有相同的奇偶性,所以定理4-8成立。
定理4-9: 设\(m,n>1\)为奇数,且\((m,n)=1\),那么
\[\left(\frac{n}{m}\right)=(-1)^{\frac{n-1}{2}\frac{m-1}{2}}\left(\frac{m}{n}\right)
\]
证明:
设\(m=\prod_{i=1}^sp_i,n=\prod_{j=1}^lq_j\),那么
\[\left(\frac{n}{m}\right)\left(\frac{m}{n}\right)=
\prod_{j=1}^l\prod_{i=1}^s\left(\frac{q_j}{p_i}\right)\cdot
\prod_{i=1}^s\prod_{j=1}^l\left(\frac{p_i}{q_j}\right)
\]
根据二次互反律
\[\left(\frac{q_j}{p_i}\right)\left(\frac{p_i}{q_j}\right)=
(-1)^{\frac{p_i-1}{2}\frac{q_j-1}{2}}
\]
所以
\[\begin{aligned}
\left(\frac{n}{m}\right)\left(\frac{m}{n}\right)&=
\prod_{j=1}^l\prod_{i=1}^s\left(\frac{q_j}{p_i}\right)\cdot
\prod_{i=1}^s\prod_{j=1}^l\left(\frac{p_i}{q_j}\right)\\
&=\prod_{j=1}^l\prod_{i=1}^s(-1)^{\frac{p_i-1}{2}\frac{q_j-1}{2}}\\
&=(-1)^E
\end{aligned}
\]
其中
\[\begin{aligned}
E&=\sum_{j=1}^l\sum_{i=1}^s{\frac{p_i-1}{2}\frac{q_j-1}{2}}\\
&=\left(\sum_{i=1}^s{\frac{p_i-1}{2}}\right)
\left(\sum_{j=1}^l\frac{q_j-1}{2}\right)
\end{aligned}
\]
根据定理4-7中的证明,我们可以知道
\[\sum_{i=1}^s{\frac{p_i-1}{2}}\equiv\frac{m-1}2\mod2\\
\sum_{j=1}^l\frac{q_j-1}{2}\equiv\frac{n-1}2\mod2
\]
于是我们得到
\[\left(\frac{n}{m}\right)\left(\frac{m}{n}\right)=(-1)^{\frac{n-1}{2}\frac{m-1}{2}}
\]
因为
\[\left(\frac{m}{n}\right)^2=(-1)^2=1
\]
因此我们就可以得到
\[\left(\frac{n}{m}\right)\left(\frac{m}{n}\right)^2=
(-1)^{\frac{n-1}{2}\frac{m-1}{2}}\left(\frac{m}{n}\right)
\Leftrightarrow
\left(\frac{n}{m}\right)=(-1)^{\frac{n-1}{2}\frac{m-1}{2}}\left(\frac{m}{n}\right)
\]
特殊情况说明:
如果\(m>1\)是奇数,而\(n\)是偶数的时候,不能直接应用定理4-9。此时我们将\(n\)写成\(n=2^\alpha{n'}\)的形式,其中\(n'\)是奇数。此时
\[\left(\frac{n}{m}\right)=\left(\frac{2^\alpha n'}{m}\right)
=\left(\frac{2}{m}\right)^\alpha\left(\frac{n'}{m}\right)
\]
这时候就可以应用雅可比符号形式下的二次互反律:
\[\left(\frac{n'}{m}\right)=(-1)^{\frac{m-1}{2}\frac{n'-1}{2}}\left(\frac{m}{n'}\right)
\]
雅可比符号和勒让德符号的关系:
通过定义可知,雅可比符号就是勒让德符号的推广,当\(m\)奇素数的时候,雅可比符号和勒让德符号等价。因此,每当需要计算勒让德符号的时候,我们总可以计算雅可比符号来代替。
4.5 二次剩余问题
上述我们讨论了模素数的二次剩余,我们总可以通过计算勒让德符号来判断一个整数是否为模奇素数的二次剩余。之后,我们将勒让德符号推广到了雅可比符号,我们自然希望能够通过计算雅可比符号来判定模一个正奇数时的二次剩余。
定义4-5: 设\(m>1\)是正奇数,且\((m,n)=1\),判断\(n\)是否为模\(m\)的二次剩余,称为二次剩余问题。
定理4-10: 当\(m\)是合数的时候,若\(n\)是模\(m\)的二次剩余,则雅可比符号满足
\[\left(\frac{n}{m}\right)=1
\]
证明:
因为\(n\)是模\(m\)的二次剩余,所以存在$x_0 $使得
\[x_0^2\equiv n\mod m\Rightarrow
\left\{\begin{aligned}
x_0^2\equiv&n\mod p_1\\
x_0^2\equiv&n\mod p_2\\
&\vdots\\
x_0^2\equiv&n\mod p_s\\
\end{aligned}\right.
\]
所以
\[\left(\frac{n}{m}\right)=\left(\frac{n}{p_1}\right)
\left(\frac{n}{p_2}\right)\cdots\left(\frac{n}{p_s}\right)=1
\]
然而定理4-10仅仅是一个必要条件,雅可比符号为1,不一定是二次剩余,例如
\[\left(\frac{2}{15}\right)=
\left(\frac{2}{3}\right)\left(\frac{2}{5}\right)=1
\]
然而,2并不是模15的二次剩余。我们将这种数称为伪二次剩余。
定理4-11: 若\(n=pq\)且\(n\)的素因子\(p,q\)已知,则\(a\)是模n的二次剩余的充要条件是
\[\left(\frac{a}{p}\right)=\left(\frac{a}{q}\right)=1
\]
必要性证明:
若\(a\)是模n的二次剩余,那么存在整数\(x_0\)使得
\[x_0^2\equiv a\mod n\Rightarrow
\left\{\begin{aligned}
x_0^2\equiv&a\mod p\\
x_0^2\equiv&a\mod q\\
\end{aligned}\right.
\]
这说明\(a\)也是模\(p,q\)的二次剩余,所以
\[\left(\frac{a}{p}\right)=\left(\frac{a}{q}\right)=1
\]
充分性证明:
因为\(a\)是模\(p,q\)的二次剩余,所以存在\(b_1,b_2\),使得
\[a\equiv b_1^2\mod p\\
a\equiv b_2^2\mod q
\]
令\(b\)满足以下同余方程组
\[\left\{\begin{aligned}
b\equiv b_1\mod p\\
b\equiv b_2\mod q\\
\end{aligned}\right.
\]
根据中国剩余定理可知,可以求出在模n意义下的唯一解\(b\)。
又因为\(b^2\equiv b_1^2\equiv a(mod\;p)\),\(b^2\equiv b_2^2\equiv a(mod\;q)\),所以
\[p|(b^2-a),\quad q|(b^2-a)
\]
并且\((p,q)=1\),根据整除的性质可知,\(p,q\)是\(b^2-a\)的两个素因子,所以
\[pq|(b^2-a)\Rightarrow n|(b^2-a)\Rightarrow a\equiv b^2\mod n
\]
故\(a\)是模n的二次剩余。


