9 数值积分

9 数值积分

9.1 引言

在数学分析中，最基本的方法便是Newton-Leibniz公式

\[\int_a^bf(x)dx=F(x)|_a^b=F(b)-F(a) \]

然而这种方法对于原函数难以求出的函数（或者根本没有初等函数形式的原函数）来说，计算其积分值过于困难。在实际应用中，我们并不需要精确求出定积分的值，而是要求计算误差小于事先给定的范围即可。

积分数值算法的基本思想是，找到被积函数\(f(x)\)的一个逼近函数\(p(x)\)，即\(f(x)=p(x)+r(x)\)，其中\(r(x)\)是误差函数。如果逼近函数的积分容易求解，那么就可以用逼近函数的积分值来近似原始被积函数的积分值。

回想黎曼积分的定义求\(\int_a^bf(x)dx\)：

1. 分割：\(a=x_0<x_1<\cdots<x_n=b\)。

2. 近似：\(\Delta{s_i}=f(\xi_i)\Delta{x_i},\Delta{x_i}=x_i-x_{i-1}\)。

3. 求和：\(S_n=\sum_{i=0}^n\Delta{s_i}\)。

4. 求极限：\(||\Delta x||=\max\{\Delta{x_i}\}\)

   \[\int_a^bf(x)dx=\lim_{||\Delta{x}||\rightarrow0}S_n=\lim_{||\Delta{x}||\rightarrow0} \sum_{i=1}^nf(\xi_i)\Delta{x_i} \]

类比上述求积分的过程，想到机械求积公式

\[\int_a^bf(x)dx=A_0f(x_0)+A_1f(x_1)+\cdots+A_nf(x_n)+R(f)=\sum_{i=0}^nA_if(x_i)+R(f) \]

其中\(A_i\)称为权系数，\(\sum_{i=0}^nA_if(x_i)\)是\(f(x_i)\)的加权和，也是积分的近似值。\(R(f)\)则称为求积余项。

我们最初的目的就是寻找\(f(x)\)的一个近似函数\(p(x)\)，从而使得

\[\int_a^bf(x)dx\approx\int_a^bp(x)dx \]

如果我们将\(p(x)\)取为拉格朗日插值多项式，那么可以得到

\[\begin{aligned} \int_a^bf(x)dx&=\int_a^b\left(\sum_{i=0}^nf(x_i)l_i(x)\right)dx+R(f)\\ &=\sum_{i=0}^nf(x_i)\int_a^bl_i(x)dx+R(f) \end{aligned}\tag{9-1-1} \]

对比机械求积公式，我们令

\[A_i=\int_a^bl_i(x)dx \]

我们称\(x_0,x_1,\cdots,x_n\)为求积节点，\(A_i\)为求积系数，可以发现如果用拉格朗日插值多项式来近似替代\(f(x)\)，那么此时求积系数\(A_i\)仅与求积节点相关，而与被积函数\(f(x)\)本身无关。

为了衡量求积公式(9-1-1)的精确程度，于是引入了代数精度，定义如下。

定义 如果求积公式(9-1-1)对于次数不超过\(m\)的多项式\(p_m(x)\)都能够准确成立，即\(R(p_m)=0\)。而至少对于一个\(m+1\)次多项式不能准确成立，则称求积公式(9-1-1)具有\(m\)次代数精度。

事实上，我们只要能够验证\(R(x^k)=0(k=0,1,\cdots,m)\)成立，而\(R(x^{m+1})\ne0\)就能够确定求积公式的代数精度为\(m\)。这是因为根据结合积分运算的性质可以得到

\[\begin{aligned} \int_a^bp_m(x)dx&=\int_a^b\left(\sum_{k=0}^m\alpha_kx^k\right)dx\\ &=\sum_{k=0}^m\alpha_k\int_a^bx^kdx \end{aligned} \]

又因为如果我们已知\(R(x^k)=0(k=0,1,\cdots,m)\)均成立，于是\(\int_a^bx^kdx\)可以由求积公式精确表达，从而求积公式对于任意次数不超过\(m\)的多项式都可以精确成立。

9.2 牛顿-柯特斯（Newton-Cotes）公式

将积分区间\([a,b]\)分成\(n\)等分，步长为\(h=(b-a)/n\)，那么求积节点为

\[x_k=a+kh,\;k=0,1,2,\cdots,n \]

做\(n\)次拉格朗日插值多项式作为\(f(x)\)的近似函数

\[L_n(x)=\sum_{k=0}^nf(x_k)l_k(x) \]

于是等距求积公式（我们将求积公式记为\(Q(f)\)）为

\[\int_a^bf(x)dx\approx Q(f)=\int_a^bL_n(x)=\sum_{k=0}^nf(x_k)\int_a^bl_k(x)dx \]

其中求积系数为

\[A_k=\int_a^bl_k(x)dx=\int_a^b\prod_{j=0\\j\ne k}^n\frac{x-x_j}{x_k-x_j}dx \]

为了求得求积系数的具体表达式，引入变换\(x=a+th\)，那么

\[\begin{aligned} A_k&=\frac{b-a}{n}\int_0^n\prod_{j\ne k}\frac{t-j}{k-j}dt\\ &=\frac{b-a}{(-1)^{n-k}k!(n-k)!n}\int_0^nt(t-1)\cdots(t-k+1)(t-k-1)\cdots(t-n)dt\\ &=(b-a)C_n^{(k)} \end{aligned} \]

其中

\[C_n^{(k)}=\frac{1}{(-1)^{n-k}k!(n-k)!n}\int_0^nt(t-1)\cdots(t-k+1)(t-k-1)\cdots(t-n)dt \]

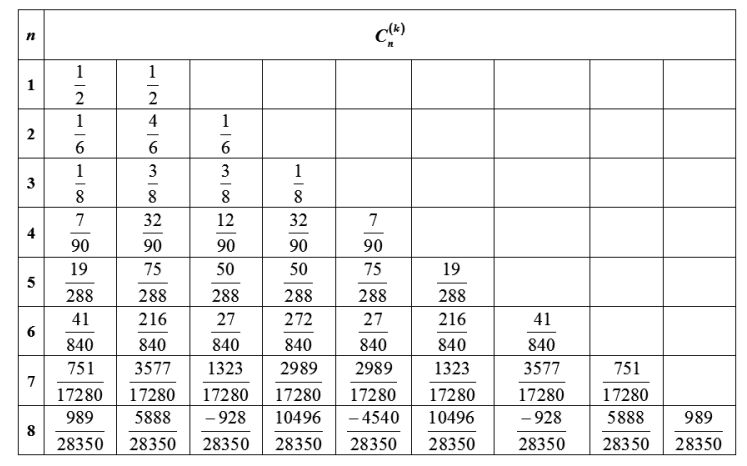
我们称\(C_n^{(k)}\)为牛顿-柯特斯系数，可以发现\(C_n^{(k)}\)只和等分区间的个数相关，而与具体的区间位置和函数值无关，因此，我们可以事先求出牛顿-柯特斯系数制成一张表，等需要的时候就可以直接查表。有了\(C_n^{(k)}\)可以将求积公式改写为

\[Q(f)=(b-a)\sum_{k=0}^nC_n^{(k)}f(x_k)\tag{9-2-1} \]

我们将式(9-2-1)称为牛顿-柯特斯公式。

牛顿-柯特斯系数的性质：

可以验证对于任意\(n\ge1\)，当\(x\in[a,b]\)时，均有\(f(x)=1\)。那么\(Q(f)=\int_a^bf(x)dx\)是严格成立的，所以

\[\int_a^bf(x)dx=b-a=(b-a)\sum_{k=0}^nC_n^{(k)} \]

于是

\[\sum_{k=0}^nC_n^{(k)}=1 \]

类似于牛顿二项式展开式的系数，牛顿-柯特斯系数也有：\(C_n^{(k)}=C_n^{(n-k)}\)，证明如下

\[C_n^{(n-k)}=\frac{1}{(-1)^{k}k!(n-k)!n}\int_0^nt(t-1)\cdots(t-n+k+1)(t-n+k-1)\cdots(t-n)dt \]

引入变换\(x=n-t\)，可以得到

\[\begin{aligned} C_n^{(n-k)}&=\frac{1}{(-1)^{k}k!(n-k)!n}\int_0^nt(t-1)\cdots(t-n+k+1)(t-n+k-1)\cdots(t-n)dt\\ &=\frac{(-1)^n}{(-1)^{k}k!(n-k)!n}\int_0^nx(x-1)\cdots(x-k+1)(x-k-1)\cdots(x-n)dx\\ &=C_n^{(k)} \end{aligned} \]

常用的牛顿-柯特斯系数表如下：

求积余项：

根据拉格朗日插值余项可知

\[R(f)=\int_a^bf(x)dx-Q(f)=\int_a^b\frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_{n+1}(x)dx \]

需要注意的这里的\(\xi\)实际上是和\(x\)相关的一个变量。

一种粗略的误差估计方式便是

\[|R(f)|\le\int_a^b\left|\frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_{n+1}(x)\right|dx \le\frac{M}{(n+1)!}(b-a)^{n+2} \]

其中\(M=\max_{a\le x\le b}|f^{(n+1)}(x)|\)。

事实上，更准确的求积余项为

\[R(f)=\left\{\begin{aligned} \frac{h^{n+3}f^{(n+2)}(\xi)}{(n+2)!}\int_a^bt^2(t-1)(t-2)\cdots(t-n)dt\quad&\text{(n is even)}\\ \frac{h^{n+2}f^{(n+1)}(\xi)}{(n+1)!}\int_a^bt(t-1)(t-2)\cdots(t-n)dt\quad&\text{(n is odd)} \end{aligned}\right. \]

其中\(\xi\in[a,b]\)。

根据上述求积余项可知，具有\(n+1\)个求积节点的牛顿-柯特斯公式至少有\(n\)次代数精度。并且当\(n\)是偶数的时候，求积公式具有\(n+1\)次代数精度。

梯形公式：

当\(n=1\)的时候，称为梯形公式：

\[Q_1(f)=\frac{(b-a)}{2}(f(a)+f(b)) \]

其几何意义就是用梯形面积代替曲边梯形的面积。

余项公式为

\[R_1(f)=-\frac{(b-a)^3}{12}f''(\xi)\quad\xi\in[a,b] \]

辛普森公式：

当\(n=2\)的时候，称为辛普森（Simpson）公式：

\[Q_2(f)=\frac{(b-a)}{6}\left(f(a)+4f\left(\frac{a+b}{2}\right)+f(b)\right) \]

其几何意义就是用抛物线围成的曲边梯形面积代替\(f(x)\)围成的曲边梯形的面积。

其余项公式为

\[R_2(f)=-\frac{(b-a)^5}{2880}f^{(4)}(\xi)\quad\xi\in[a,b] \]

辛普森3/8公式：

当\(n=3\)的时候，称为辛普森3/8公式

\[Q_3(f)=\frac{(b-a)}{8}(f(a)+3f(a+h)+3f(a+2h)+f(b)) \]

其中\(h=(b-a)/3\)。

柯特斯公式：

当\(n=4\)的时候，称为柯特斯公式：

\[Q_4(f)=\frac{(b-a)}{90}(7f(a)+32f(a+h)+12f(a+2h)+32f(a+3h)+7f(b)) \]

其中\(h=(b-a)/4\)。

牛顿-柯特斯公式的数值稳定性：

假设计算\(f(x_k)\)的舍入误差为\(\varepsilon_k\)，且计算\(C_n^{(k)}\)时没有误差，那么计算\((b-a)\sum_kC_n^{(k)}f(x_k)\)产生的误差为

\[\eta_n=(b-a)\sum_{k=0}^nC_n^{(k)}\varepsilon_k \]

因此

\[|\eta_n|\le(b-a)\sum_{k=0}^n|C_n^{(k)}|\varepsilon \]

其中\(\varepsilon=\max|\varepsilon_k|\)。

当牛顿-柯特斯系数都是正数时，可以得到\(|\eta_n|\le(b-a)\varepsilon\)，此时误差增长是线性的。从而当牛顿-柯特斯系数恒为正数时，求积公式是数值稳定的。

当牛顿-柯特斯系数出现负数的时候，\(\sum_{k=0}^n|C_n^{(k)}|\)会随着\(n\)的增加而增加，从而舍入误差会随着\(n\)的增加而增加。从牛顿-柯特斯系数表可以看到当\(n\ge8\)的时候，出现了负的系数，因此当\(n\ge8\)的时候，牛顿-柯特斯公式是不使用的。

9.3 复化求积公式

根据梯形、辛普森、柯特斯求积余项可知，随着求积节点的点数增多，对应公式的精度也会提高。但当\(n\ge8\)的时候，牛顿-柯特斯系数出现负值。根据之前误差分析，当积分公式出现负系数时，可能导致舍入误差增大，并且难以估计。因此不能通过增加求积节点的个数来增加精度，在实际应用中常把积分区间分成若干个，然后在每个小区间上应用低阶求积公式，最后求和得到整个区间上的求积公式。这就是复化求积公式的基本思想。

复化求积公式克服了高次牛顿-柯特斯公式数值不稳定性，并且运算简单容易编程实现。常用的复化求积公式是复化梯形公式和复化抛物线公式。

复化梯形公式：

将区间\([a,b]\)划分成n等分，其中求积节点为\(x_k=a+kh,k=0,1,\cdots,n\)，步长\(h=(b-a)/n\)。然后在每一个小区间上应用梯形公式，最后累加起来，即

\[\int_a^bf(x)dx\approx\sum_{k=0}^{n-1}\frac{h}{2}(f(x_k)+f(x_{k+1}))= \frac{h}{2}\left(f(a)+2\sum_{k=1}^{n-1}f(x_k)+f(b)\right) \]

在区间\([x_k,x_{k+1}]\)区间上的余项为

\[-\frac{h^3}{12}f''(\xi_k) \]

复化梯形公式的余项为

\[\begin{aligned} R_n(f)&=-\frac{h^3}{12}\left(f''(\xi_1)+f''(\xi_2)+\cdots+f''(\xi_n)\right)\\ &=-\frac{nh^3}{12}\left(\frac{f''(\xi_1)+f''(\xi_2)+\cdots+f''(\xi_n)}n\right)\\ &=-\frac{nh^3}{12}f''(\xi)\\ &=-\frac{(b-a)^3}{12n^2}f''(\xi) \end{aligned} \]

其中\(\xi\in[a,b]\)。上述式子之所以成立，是因为

\[m\le\frac{f''(\xi_1)+f''(\xi_2)+\cdots+f''(\xi_n)}n\le M \]

其中\(m=\min_k f''(\xi_k),M=\max_kf''(\xi_k)\)。若\(f''(x)\)在\([a,b]\)上是连续的，那么肯定存在一个\(\xi\in[a,b]\)使得

\[m\le f''(\xi)\le M \]

复化辛普森公式：

将积分区间\([a,b]\)进行\(2n\)等分，每个小区间的长度为\(h=(b-a)/(2n)\)，在\([x_{2k-2},x_{2k}]\)上应用辛普森公式，那么

\[\begin{aligned} \int_a^bf(x)dx&\approx\frac{2h}{6}\sum_{k=1}^{n} \left[f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})\right]\\ &=\frac{b-a}{6n}\left(f(a)+f(b)+4\sum_{k=1}^nf(x_{2k-1})+2\sum_{k=1}^{n-1}f(x_{2k})\right) \end{aligned} \]

复化辛普森公式的余项为

\[\begin{aligned} R_n(f)&=-\frac{(2h)^5}{2880}\left(f^{(4)}(\xi_1)+f^{(4)}(\xi_2)+\cdots+f^{(4)}(\xi_n)\right)\\ &=-\frac{nh^5}{90}\left(\frac{f^{(4)}(\xi_1)+f^{(4)}(\xi_2)+\cdots+f^{(4)}(\xi_n)}n\right)\\ &=-\frac{nh^5}{90}f^{(4)}(\xi) \end{aligned} \]

9.4 外推法

理查森（Richarson）外推法：

在数值计算中，常用一个序列\(f_1,f_2,\cdots\)去逼近一个\(f^*\)，并在理论上估计余项（误差）。一个有趣的问题是能够在误差估计的基础之上，从已有的序列\(f_1,f_2,\cdots\)产生一个新的序列\(\{f_i^{(1)}\}\)能够比\(\{f_i\}\)更快收敛到\(f^*\)。这就是数值计算中的外推法，这时加速收敛的一个重要技巧。

假设有一个待求量\(F^*\)，使用一个步长\(h\)的函数\(F_1(h)\)去逼近\(F^*\)，并且\(F^*\)和\(h\)无关。当\(h\rightarrow0\)时，\(F_1(h)\rightarrow F^*\)，并且\(F_1(h)\)逼近\(F^*\)的截断误差的估计式为：

\[R(F^*)=F^*-F_1(h)=a_1^{(1)}h^{P_1}+a_2^{(1)}h^{P_2}+\cdots+a_n^{(1)}h^{P_n}+\cdots\tag{9-4-1} \]

其中\(0<P_1<P_2<\cdots<P_n<\cdots,a_i^{(1)}(i=1,2,\cdots)\)都是与\(h\)无关的常数。

上述式子说明\(F_1(h)\)逼近\(F^*\)的阶是\(h^{P_1}\)，我们的目标就是通过\(F_1(h)\)构造出一个新的序列，这个新的序列逼近\(F^*\)的阶比\(h^{P_1}\)更高，比如\(h^{P_2}\)。

构造方法如下，其中\(q\ne0\)，那么

\[\begin{aligned} F^*-F_1(qh)&=a_1^{(1)}(qh)^{P_1}+a_2^{(1)}(qh)^{P_2}+\cdots+a_n^{(1)}(qh)^{P_n}+\cdots\\ &=a_1^{(1)}q^{P_1}h^{P_1}+a_2^{(1)}q^{P_2}h^{P_2}+\cdots+a_n^{(1)}q^{P_n}h^{P_n}+\cdots \end{aligned}\tag{9-4-2} \]

用等式(9-4-1)两侧乘以\(q^{P_1}\)，然后减去式(9-4-2)，即

\[(q^{P_1}-1)F^*-(q^{P_1}F_1(h)-F_1(qh))=a_2^{(1)}(q^{P_1}-q^{P_2})h^{P_2}+ a_3^{(1)}(q^{P_1}-q^{P_3})h^{P_3}+\cdots \]

于是

\[F^*-\frac{q^{P_1}F_1(h)-F_1(qh)}{q^{P_1}-1}=a_2^{(2)}h^{P_2}+a_3^{(2)}h^{P_3}+\cdots+ a_n^{(2)}h^{P_n}+\cdots \]

其中

\[a_k^{(2)}=a_k^{(1)}\frac{q^{P_1}-q^{P_k}}{q^{P_1}-1},\quad k=2,3,\cdots,n,\cdots \]

令

\[F_2(h)=\frac{q^{P_1}F_1(h)-F_1(qh)}{q^{P_1}-1} \]

根据上述推导出来的余项可知，\(F_2(h)\)逼近\(F^*\)的误差为\(h^{P_2}\)。

依据上面的推导方法，我们最终可以构造出

\[\begin{aligned} F_m(h)=\frac{q^{P_{m-1}}F_{m-1}(h)-F_{m-1}(qh)}{q^{P_{m-1}}-1}\\ F^*-F_m(h)=a_m^{(m)}h^{P_m}+O(h^{P_m}) \end{aligned}\quad m=1,2,\cdots \]

可以知道\(F_m(h)\)逼近\(F^*\)的阶是\(h^{P_m}\)。这种方法称为理查森外推法。

龙贝格（Romberg）算法：

龙贝格算法是以复化梯形公式为基础，然后应用理查森外推法得到的算法。在数学上已经证明复化梯形公式\(T_1(h)\)和定积分\(I=\int_a^bf(x)dx\)之间的误差余项可以表示为

\[I-T_1(h)=a_2h^2+a_4h^4+a_6h^6+\cdots \]

其中\(h\)是每个小区间的长度，\(a_k\)是与\(h\)无关的系数。

使用一次外推法，取\(q=1/2\)，可以得到

\[T_1\left(\frac{h}2\right)=a_2\left(\frac{h}2\right)^2+a_4\left(\frac{h}2\right)^4+\cdots \]

于是

\[T_2(h)=\frac{4T_1(h/2)-T_1(h)}{4-1} \]

可以发现此时\(T_2(h)\)的误差的阶从\(O(h^2)\)变成了\(O(h^4)\)。事实上，如果利用复化梯形公式计算\(T_1(h)\)和\(T_1(h/2)\)之后，可以验证\(T_2(h)\)实际上就是复化辛普森公式。

重复上述过程就可以得到

\[T_m(h)=\frac{4^{m-1}T_{m-1}(h/2)-T_{m-1}(h)}{4^{m-1}-1} \]

并且\(I-T_m(h)=a_{2m}^{(m)}h^{2m}+O(h^{2m})\)。

可以发现上述龙贝格求积算法就是每次将区间缩小一半，因此上述算法也称为逐次分半加速收敛法。

在龙贝格求积算法中，我们将复化梯形公式表示为

\[T_1^{(j)}=T_1(\frac{b-a}{2^j})\quad j=0,1,2,\cdots \]

其中\((b-a)/2^j\)是每一个区间的长度，相当于将\([a,b]\)区间划分成了\(2^j\)个小区间。

使用\(k\)表示外推指标，即

\[T_{k+1}^{(j)}=\frac{4^kT_k^{(j+1)}-T_k^{(j)}}{4^k-1},\quad k=1,2,\cdots \]

可以将整个计算过程列表示意：

求积过程可以被表述为：

1. 初始化参数：\(k=2,\varepsilon,T_1^{(0)}\)。
2. 计算\(T_1^{(k-1)}\)。
3. 依次计算：\(T_{2}^{(k-2)},T_3^{(k-3)},\cdots,T_k^{(0)}\)。
4. 如果\(|T_k^{(0)}-T_{k-1}^{(0)}|<\varepsilon\)，则返回\(T_k^{(0)}\)。否则，执行下一步。
5. \(k=k+1\)，返回2继续执行。

上述算法只有在达到实现给定的精度算法才会停止，也可以通过定义最大外推指标控制外推的次数。