4 线性方程组的直接解法
4.1 引言
在自然科学和工程计算的很多问题通常都可以归结为求解线性方程组的问题,如三次样条插值、最小二乘法拟合曲线等等。因此,在本章中将探讨线性方程组的直接解法。
一般的n元线性方程组具有以下形式:
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2&+\cdots+a_{1n}x_n=b_1\\
a_{21}x_1+a_{22}x_2&+\cdots+a_{2n}x_n=b_2\\
&\cdots\\
a_{n1}x_1+a_{n2}x_2&+\cdots+a_{nn}x_n=b_n
\end{aligned}\right.
\]
写成矩阵的形式就是:\(Ax=b\)
其中
\[A=\left[\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\vdots&\vdots&\ddots&\vdots\\
a_{n1}&a_{n2}&\cdots&a_{nn}\\
\end{matrix}\right],
x=\left[\begin{matrix}
x_1\\x_2\\\vdots\\x_n
\end{matrix}\right]
,b=\left[\begin{matrix}
b_1\\b_2\\\vdots\\b_n
\end{matrix}\right]
\]
如果线性方程组的系数行列式不为零,即\(\det(A)\ne0\),那么该方程有唯一解。根据克莱姆(Gramer)法则,方程的解为
\[x_i=\frac{\det{A_i}}{\det{A}},i=1,2,\cdots,n
\]
如果使用克莱姆法则求解,那么一共需要计算\(n+1\)个\(n\)阶行列式,并进行\(n\)次除法。计算一个\(n\)阶行列式需要\((n-1)\times n!\)次乘法,总的计算量就是\(n+(n-1)(n+1)!\),当\(n\)的值比较大的时候,需要执行的浮点数计算次数过于巨大,因此在实际中是不可行的。
关于线性方程组的数值解法一般有两类:
- 直接法:经过有限步运算,求得方程组的精确解(如果不考虑计算过程中的舍入误差)
- 迭代法:用某种极限过程去逼近线性方程组的精确解,程序设计比较简单,但存在收敛性和收敛速度等问题。
4.2 消元法
4.2.1 三角形方程组
首先,介绍两种最简单方程组形式:上三角形方程组、下三角形方程组。实际上消元法的目的就是将一般的方程组转化为三角形方程组进行求解。
上三角形方程组的一般形式为:
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n&=b_1\\
a_{22}x_2+\cdots+a_{2n}x_n&=b_2\\
\vdots&\\
a_{nn}x_n&=b_n
\end{aligned}\right.
\]
其中\(a_{ii}\ne0(i=1,2,\cdots,n)\)。
为了求解上三角形方程组,我们先求解出\(x_n=b_n/a_{nn}\),然后就可以从下至上利用已经求出的\(x_k\),依次求出\(x_{n-1},\cdots,x_1\)的值,这就完成了上三角形方程组的求解。整个求解过程可以被描述为:
\[\left\{\begin{aligned}
x_n&=\frac{b_n}{a_{nn}}\\
x_i&=\frac{1}{a_{ii}}(b_i-\sum_{k=i+1}^n{a_{ik}x_k}), (i=n-1,\cdots,2,1)
\end{aligned}\right.
\]
上述求解过程称为回代,因此也将这种方法称为回代法。整个过程需要进行乘法次数计算如下
\[1+2+\cdots+(n-2)+(n-1)=\frac{n(n-1)}2
\]
需要执行的除法次数为\(n\)次,那么一共就需要\(n(n+1)/2\)次浮点运算。
同理,对于下三角形方程组的求解方法为
\[\left\{\begin{aligned}
x_1&=\frac{b_1}{a_{11}}\\
x_i&=\frac{1}{a_{ii}}(b_i-\sum_{k=1}^{i-1}{a_{ik}x_k}), (i=2,3,\cdots,n-1)
\end{aligned}\right.
\]
所需的浮点运算次数和求解上三角形方程组相同。
4.2.2 高斯消元法
消元法的基本思想就是对方程组进行初等变换,把一般形式的方程组转化为容易求解的三角形方程组。基本过程就是先将一般的线性方程组转换成通解的上三角形方程组(这个过程称为消元),然后利用回代法即可求解原方程组的解。
消元过程如下所示:
假设现有一个\(n\)阶方程组(\(a_{11}\ne0\)):
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2&+\cdots+a_{1n}x_n=b_1\\
a_{21}x_1+a_{22}x_2&+\cdots+a_{2n}x_n=b_2\\
&\cdots\\
a_{n1}x_1+a_{n2}x_2&+\cdots+a_{nn}x_n=b_n
\end{aligned}\right.
\]
令\(m_{i1}=-a_{i1}/a_{11}\),用\(m_{i1}\)乘以第一个方程,然后加到第\(i\)个方程上,得到
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2&+\cdots+a_{1n}x_n=b_1\\
a_{22}^{(1)}x_2&+\cdots+a_{2n}^{(1)}x_n=b_2^{(1)}\\
&\cdots\\
a_{n2}^{(1)}x_2&+\cdots+a_{nn}^{(1)}x_n=b_n^{(1)}
\end{aligned}\right.
\]
其中\(a_{ij}^{(1)}=a_{ij}+a_{1j}m_{i1},b_i^{(1)}=b_i+b_1m_{i1}(i,j=2,3,\cdots,n)\)。
如果\(a_{22}^{(1)}\ne0\),则保留前两个方程。与上一步类似,进一步进行消元,得到
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2+a_{13}x_3+\cdots+a_{1n}x_n&=b_1\\
a_{22}^{(1)}x_2+a_{23}^{(1)}x_3+\cdots+a_{2n}^{(1)}x_n&=b_2^{(1)}\\
a_{33}^{(2)}x_3+\cdots+a_{3n}^{(2)}x_n&=b_3^{(2)}\\
\vdots&\\
a_{n3}^{(2)}x_2+\cdots+a_{nn}^{(2)}x_n&=b_n^{(2)}
\end{aligned}\right.
\]
其中\(a_{ij}^{(1)}=a_{ij}^{(1)}+a_{2j}m_{i2},b_i^{(2)}=b_i^{(1)}+b_2^{(1)}m_{i2}(i,j=3,4,\cdots,n),m_{i2}=-a^{(1)}_{i2}/a_{22}^{(1)}\)。
不断重复上述过程,最终可以得到等价的上三角方程组:
\[\left\{\begin{aligned}
a_{11}x_1+a_{12}x_2+a_{13}x_3+\cdots+a_{1n}x_n&=b_1\\
a_{22}^{(1)}x_2+a_{23}^{(1)}x_3+\cdots+a_{2n}^{(1)}x_n&=b_2^{(1)}\\
a_{33}^{(2)}x_3+\cdots+a_{3n}^{(2)}x_n&=b_3^{(2)}\\
\vdots&\\
a_{nn}^{(n-1)}x_n&=b_n^{(n-1)}
\end{aligned}\right.
\]
此时就可以使用回代法进行求解。
现在我们来考虑进行消元所需要执行的乘除操作次数。考虑第\(k\)步消元时所需要的操作,首先,计算\(m_{ik}(i=k+1,\cdots,n)\)需要\(n-k\)次除法。然后,将第\(k\)个方程乘以\(m_{ik}\)需要\(n-k+1\)次乘法(不是\(n-k+2\),因为\(a_{kk}^{(k-1)}\)下方的数均是0,可以直接赋值不需要实际计算)。因为一共有\(n-k\)个方程,所以最终所需的浮点操作为\((n-k)+(n-k)(n-k+1)\)。消元步骤一共执行\(n-1\)次,所以全部消元过程所需的乘除操作次数为
\[\sum_{k=1}^{n-1}=[(n-k)+(n-k)(n-k+1)]=\frac{1}{6}n(n-1)(2n+5)
\]
而回代过程所需的乘除操作次数为\(n(n+1)/2\),所以高斯消元法所需的总计算量为
\[N=\frac{1}{6}n(n-1)(2n+5)+\frac{n(n+1)}{2}=\frac{1}{3}n(n^2+3n-1)
\]
因此计算复杂度为\(O(n^3)\),所以采用高斯消元法的计算量将远小于使用克莱姆法则所需的计算量。
这里还需要主要的问题是,在上述高斯消元的过程中,我们是从上至下顺序进行的,这就要求在\(a_{kk}^{(k-1)}\)处的值不等于0,即对系数矩阵主对角线上的元素不为零。换句话说,如果高斯消元法能够顺利进行就需要保证:\(a_{kk}^{(k-1)}\ne0,k=1,2,\cdots,n\)。
考虑系数矩阵\(A\)的顺序主子矩阵的行列式:
\[\det A_k=\left|\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1k}\\
a_{21}&a_{22}&\cdots&a_{2k}\\
\vdots&\vdots&\ddots&\vdots\\
a_{k1}&a_{k2}&\cdots&a_{kk}\\
\end{matrix}\right|=
\left|\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1k}\\
0&a_{22}^{(1)}&\cdots&a_{2k}^{(1)}\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&a_{kk}^{(k-1)}\\
\end{matrix}\right|=
a_{11}a_{22}^{(1)}\cdots a_{kk}^{(k-1)}
\]
其中\(k=1,2,\cdots,n\)。
如果\(A\)所有的顺序主子式\(\det A_k\ne0\),就可以保证在\(a_{kk}^{(k-1)}\)处的值不等于0,反之亦然。因此顺序高斯消元法可行的充要条件为\(A\)的所有顺序主子式均不为0。
4.2.3 列主元消元
上述高斯消元法存在一定的问题,下面给出两个例子:
例题1 使用高斯消元法求解如下方程组:
\[\left\{\begin{aligned}
2x_2=1\\
2x_1+3x_2=2
\end{aligned}\right.
\]
此时\(a_{11}=0\),不能直接使用高斯消元法。需要先交换两个方程的位置才行。
例题2 假设我们在,只能表示四位浮点十进制数计算机上计算下列方程组
\[\left\{\begin{aligned}
0.0001x_1+x_2=1\\
x_1+x_2=2
\end{aligned}\right.
\]
本题在计算机内部表示为
\[\left\{\begin{aligned}
0.1000\times10^{-3}x_1+0.1000\times10^1x_2&=0.1000\times10^1\\
0.1000\times10^1x_1+0.1000\times10^1x_2&=0.2000\times10^1
\end{aligned}\right.
\]
此时是可以直接使用高斯消元法的,因为\(a_{11}\ne0,m_{21}=-10^4\),所以
\[\begin{aligned}
a_{22}^{(1)}&=0.1000\times10^1-10^4\times0.1000\times10^1\\
&=0.00001\times10^5-0.1000\times10^5\\
&=0.0000-0.1000\times10^5\\
&=-0.1000\times10^5
\end{aligned}
\]
由于浮点数计算时,需要进行对阶,这使得小数被大数“吃掉了”。同理我们可以得到
\[b_2^{(1)}=-0.1000\times10^5
\]
于是得到三角方程组
\[\left\{\begin{aligned}
0.1000\times10^{-3}x_1+0.1000\times10^1x_2&=0.1000\times10^1\\
-0.1000\times10^5x_2&=-0.1000\times10^5
\end{aligned}\right.
\]
通过回代可以解得\(x_2=1,x_1=0\)。
然而原方程的实际解为\(x_2=9998/9999,x_1=10000/9999\),因此此题如果直接使用高斯消元法将会导致解严重失真。导致这个问题出现的原因在于消元过程中除了一个很小的数使得最后的结果非常大,这可能导致出现大数吃小数的现象,如果原问题是病态的将会导致最终结果严重偏离理想值。
为了解决这个问题,将引入选主元消元法,避免除以一个很小的数。在高斯消元过程中,我们将\(a_{kk}^{(k-1)}\)位置称为主元位置,位于该位置的元素则称为主元素。如果在进行第\(k\)步消元时,将第\(k\)列中绝对值最大的元素作为主元素,将其调换到第\(k\)行在做消元,这种方法就称为列主元消元。具体方法如下:
- 先在第一列选取绝对值最大的元素:\(|a_{m1}|=\max\{|a_{11}|,|a_{21}|,\cdots,|a_{n1}|\}\)。交换第1行和第m行的所有元素(即交换第1个方程和第m个方程的位置),在做消元。
- 进行第\(k(\ge2)\)步消元前,在选取第\(k\)列绝对值最大的元素:\(|a_{mk}^{(k-1)}|=\max\{|a_{kk}^{(k-1)}|,|a_{(k+1)k}^{(k-1)}|,\cdots,|a_{nk}^{(k-1)}|\}\)。交换第1行和第m行的所有元素(即交换第k个方程和第m个方程的位置),在做消元。
与高斯消元法相比,列主元消元只是在每一步消元之前都增加了选主元和交换方程位置的操作,并不会影响最终的结果。
4.2.4 全主元消元
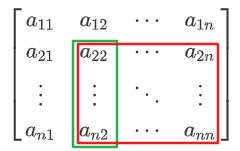
以第\(k\)步消元为例,列主元消元关注的仅仅只是\(a_{kk}^{(k-1)}\)及其下方的元素,而全主元关注的是以\(a_{kk}^{(k-1)}\)作为第一行第一列元素的右下子矩阵的所有元素,因此寻找主元的位置更广。
![]()
如上图所示,绿色框内表示列主元消元关注的范围,红色框内表示全主元关注的范围。
在执行第\(k\)步消元前,首先,需要在右下子矩阵中选择绝对值最大的元素作为主元素:
\[|a_{pq}^{(k-1)}|=\max_{k\le i,j\le n}|a_{ij}^{(k-1)}|
\]
选定好主元素后,就涉及到上下方向方程位置的互换,以及左右方向未知数位置的互换:
- 若\(p\ne k\),则交换第\(k\)行和第\(p\)行。
- 若\(q\ne k\),则交换第\(q\)列和第\(k\)列。
最后,执行消元操作。
注意: 由于列交换改变了未知数\(x_i\)的顺序,因此每交换一次,就需要做一次记录,等求出最终结果之后再交换回来。
4.3 矩阵的分解
4.3.1 LU分解
LU分解的目的是将一个矩阵\(A\)分解成一个下三角阵\(L\),和上三角阵\(U\)。一旦求得\(A=LU\),则方程\(Ax=b\)就可以转化为求解\(LUx=b\),令\(Ux=y\),则\(Ly=b\)。实际求解过程如下:
- 由\(Ly=b\)求解出\(y\)。
- 再由\(Ux=y\)求解出\(x\)。
矩阵\(A\)能够进行LU分解的充要条件是\(A\)的各阶主子式不为零,这可以理解为LU分解是通过高斯消元法诱导出来的。
矩阵的LU分解一共有两种形式:
- 多利特尔(Doolittle)分解:\(L\)为单位下三角阵(主对角线值全为1),\(U\)为上三角阵。
- 库朗(Crout)分解:\(L\)为下三角阵,\(U\)为单位上三角阵(主对角线值全为1)。
在这里我们只考虑多利特尔分解,下面我们将通过高斯消元法的观点推导出矩阵的LU分解。
假设\(A\in\mathbb{R}^{3\times3}\)。高斯消元法的每一步消元操作都等价于左乘一个矩阵做初等行变换,首先,考虑第一次消元:
\[L_1=\left[\begin{matrix}
1&0&0\\m_{21}&1&0\\m_{31}&0&1
\end{matrix}\right],m_{i1}=-a_{i1}/a_{11},i=2,3
\]
于是我们有
\[L_1A=\left[\begin{matrix}
1&0&0\\m_{21}&1&0\\m_{31}&0&1
\end{matrix}\right]
\left[\begin{matrix}
a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}
\end{matrix}\right]=
\left[\begin{matrix}
a_{11}&a_{12}&a_{13}\\&a_{22}^{(1)}&a_{23}^{(1)}\\&a_{32}^{(1)}&a_{33}^{(1)}
\end{matrix}\right]
\]
进行第二次消元
\[L_2=\left[\begin{matrix}
1&0&0\\0&1&0\\0&m_{32}&1
\end{matrix}\right],m_{i2}=-a_{i2}/a_{22},i=3
\]
可以得到
\[L_2L_1A=
\left[\begin{matrix}
1&0&0\\0&1&0\\0&m_{32}&1
\end{matrix}\right]
\left[\begin{matrix}
a_{11}&a_{12}&a_{13}\\&a_{22}^{(1)}&a_{23}^{(1)}\\&a_{32}^{(1)}&a_{33}^{(1)}
\end{matrix}\right]=
\left[\begin{matrix}
a_{11}&a_{12}&a_{13}\\&a_{22}^{(1)}&a_{23}^{(1)}\\&&a_{33}^{(2)}
\end{matrix}\right]=U
\]
根据线性代数中的知识,我们知道初等行变换都是可逆的。因此\(L_1,L_2\)都是可逆矩阵,所以
\[A=L_1^{-1}L_2^{-1}U=
\left[\begin{matrix}
1&0&0\\-m_{21}&1&0\\-m_{31}&0&1
\end{matrix}\right]
\left[\begin{matrix}
1&0&0\\0&1&0\\0&-m_{32}&1
\end{matrix}\right]U=
\left[\begin{matrix}
1&0&0\\-m_{21}&1&0\\-m_{31}&-m_{32}&1
\end{matrix}\right]U
\]
至此,我们已经成功对\(A\)进行了LU分解
\[L=\left[\begin{matrix}
1&0&0\\-m_{21}&1&0\\-m_{31}&-m_{32}&1
\end{matrix}\right],
U=\left[\begin{matrix}
a_{11}&a_{12}&a_{13}\\&a_{22}^{(1)}&a_{23}^{(1)}\\&&a_{33}^{(2)}
\end{matrix}\right]
\]
上述分析对于一般的\(n\)阶矩阵都是适用的,但需要注意的是,LU分解是通过高斯消元法推导出来的,因此只有当\(A\)满足顺序主子式均大于零的时候,才能够进行LU分解。上述过程涉及到一个小知识点:两个下三角阵的乘积一定还是下三角阵。
在编程实现LU分解时,通过上述推导可以发现,在构造上三角阵\(U\)的时候,也可以同时得到下三角阵\(L\)。也就是说,当我们执行第\(k\)步高斯消元法,将\(a_{kk}^{(k-1)}\)下方的元素变成0时,需要先计算\(m_{ik}(i=k+1,\cdots,n)\),此时就可以同时得到\(L\)的第\(k\)列元素\(-m_{ik}\),而不需要单独去求解\(L\)。
4.3.2 追赶法
在工程计算中,经常会遇到如下特殊的三对角线方程组:
\[Ax=\left[\begin{matrix}
b_1&c_1&&&\\a_2&b_2&c_2&&\\
&\ddots&\ddots&\ddots&\\
&&a_{n-1}&b_{n-1}&c_{n-1}\\
&&&a_n&b_n
\end{matrix}\right]
\left[\begin{matrix}
x_1\\x_2\\\vdots\\x_{n-1}\\x_n
\end{matrix}\right]=
\left[\begin{matrix}
d_1\\d_2\\\vdots\\d_{n-1}\\d_n
\end{matrix}\right]=d
\]
所谓追赶法就是将LU分解应用到上述系数矩阵,从而得到的一个特殊解法。
首先对系数矩阵进行一个简单的分析,如果对\(A\)进行高斯消元,可以发现所有\(c_i(1\le i\le n-1)\)的上方都是0,这意味着消元过程中,主对角线上方的三角形区域会完全保留在\(U\)中。
其次,主对角线下方只有\(a_i(2\le i\le n)\)需要消去,因此,第\(k\)步消元只需要计算\(m_{(k+1)k}\),这意味着\(L\)下方只有紧挨着主对角线的元素不为0,其余均为0。
综上分析,可以得到系数矩阵\(A\)的LU分解形式:
\[\left[\begin{matrix}
b_1&c_1&&&\\a_2&b_2&c_2&&\\
&\ddots&\ddots&\ddots&\\
&&a_{n-1}&b_{n-1}&c_{n-1}\\
&&&a_n&b_n
\end{matrix}\right]=
\left[\begin{matrix}
1&&&&\\p_2&1&&&\\
&\ddots&\ddots&&\\
&&p_{n-1}&1&\\
&&&p_n&1
\end{matrix}\right]
\left[\begin{matrix}
q_1&c_1&&&\\&q_2&c_2&&\\
&&\ddots&\ddots&\\
&&&q_{n-1}&c_{n-1}\\
&&&&q_n
\end{matrix}\right]
\]
分析\(A\)的第\(k\)行如何通过右侧两个矩阵的乘积得到,根据矩阵分块的知识,可以知道
\[\left[\begin{matrix}
\cdots&\cdots&a_{k}&b_k&c_k&\cdots
\end{matrix}\right]=
\left[\begin{matrix}
\cdots&\cdots&p_kq_{k-1}&p_kc_{k-1}+q_k&c_k&\cdots
\end{matrix}\right]
\]
上述省略号代表0,于是
\[a_k=p_kq_{k-1}\\
b_k=p_kc_{k-1}+q_k
\]
可以验证对于\(2\le k\le n\),上述式子都是成立的,并且\(q_1=b_1\)。综上可得追赶法计算公式:
\[\left\{\begin{aligned}
q_1&=b_1\\
p_k&=\frac{a_k}{q_{k-1}}\\
q_k&=b_k-p_kc_{k-1}
\end{aligned}\right.k=2,3,\dots,n
\]
追赶法名称的由来可能就是因为需要交替计算\(p_k,q_k\),这相当于是\(p,q\)两个下标之间在相互追赶。
求解\(Ly=d\)
\[\left[\begin{matrix}
1&&&&\\p_2&1&&&\\
&\ddots&\ddots&&\\
&&p_{n-1}&1&\\
&&&p_n&1
\end{matrix}\right]\left[\begin{matrix}
y_1\\y_2\\\vdots\\y_{n-1}\\y_n
\end{matrix}\right]=
\left[\begin{matrix}
d_1\\d_2\\\vdots\\d_{n-1}\\d_n
\end{matrix}\right]\Rightarrow
\left\{\begin{aligned}
y_1&=d_1\\
p_2y_1+y_2&=d_2\\
\vdots&\\
p_ky_{k-1}+y_k&=d_k\\
\vdots&\\
p_ny_{n-1}+y_n&=d_n
\end{aligned}\right.
\]
因此
\[\left\{\begin{aligned}
y_1&=d_1\\
y_k&=d_k-p_ky_{k-1}
\end{aligned}\right.k=2,3,\cdots,n
\]
求解\(Ux=y\)
\[\left[\begin{matrix}
q_1&c_1&&&\\&q_2&c_2&&\\
&&\ddots&\ddots&\\
&&&q_{n-1}&c_{n-1}\\
&&&&q_n
\end{matrix}\right]
\left[\begin{matrix}
x_1\\x_2\\\vdots\\x_{n-1}\\x_n
\end{matrix}\right]
=
\left[\begin{matrix}
y_1\\y_2\\\vdots\\y_{n-1}\\y_n
\end{matrix}\right]
\Rightarrow
\left\{\begin{aligned}
q_1x_1+c_1x_2&=y_1\\
\vdots&\\
q_kx_k+c_kx_{k+1}&=y_k\\
\vdots&\\
q_nx_n&=y_n
\end{aligned}\right.
\]
因此
\[\left\{\begin{aligned}
x_n&=y_n/q_n\\
x_k&=(y_k-c_kx_{k+1})/q_k
\end{aligned}\right.k=n-1,n-2,\cdots,1
\]
综上可知,使用追赶法求解三对角线方程时,不需要真的去求解系数矩阵的LU分解,只需要根据上述的递推公式就可以直接求问题的解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号