4 禁忌搜索
4 禁忌搜索
4.1 概述
禁忌搜索(Tabu Search,TS)是美国科罗拉多州大学的Fred Glover教授于1986年提出的搜索算法,是一个可以用来跳出局部最优的搜索方法。TS从一个初始解出发,按照一定的策略往一个方向进行搜索。同时为了避免局部最小值TS还引入了“记忆机制”,记住已经选过的解,如果下次出现了在自己记忆中出现过的解,TS就不会去选择它,当然经过了一段时间后,记忆中较老的解将会被遗忘。
在TS中,这个记忆机制就称为禁忌表,在禁忌表中的解表明该解先前已经被选择过了,禁止被重复选择。而遗忘操作则是将解从禁忌表中删除。
4.2 具体算法细节
这里通过一个4个城市的对称TSP问题来说明禁忌搜索的具体细节:
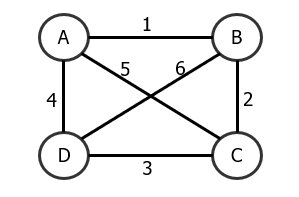
解形式的定义:
我们将解定义为A,B,C,D组成的字符序列,即\(ABCD\)表示从A城市出发,先经过B,然后经过C,再经过D,最后回到城市A。
解的形式依赖于具体的问题,不同解的定义将直接影响到后续算法的实现。
新解(邻域)的产生:
这里我们定义一个邻域产生函数\(candidate(\cdot)\),该函数接受一个序列,然后输出该序列的邻域。为了产生新的解,我们需要定义一个解相邻的解应该是怎么样的。一种可行的方式是将当前的解两个相邻的城市互换得到新的解,即\(ABCD\)的邻域为
当然也可以选择其他方式产生新的解。
禁忌表设置:
禁忌表的两个重要因素是禁忌对象(被放入到禁忌表中的对象)以及禁忌长度(禁忌对象多长时间后从禁忌表中移除)。这里我们将禁忌对象选取为问题的解,禁忌长度设置为2。
初始化禁忌表\(H=\emptyset\),以及一个初始解\(x=ABCD\),历史最优解初始化为\(x_b=ABCD\),代价记为\(cost_b=10\)。
(1)第一次迭代
先产生当前解的邻域\(candidate(ABCD)=\{BACD,ACBD,ABDC\}\),然后选择该邻域内代价最小的解\(BACD\),其代价为13,所以不更新历史最优解。最后,更新禁忌表\(H=\{(BACD,2)\}\),这里禁忌表中的数字每经过一次迭代数字减一,归零时移除相应的禁忌对象。
(2)第二次迭代
先产生当前解的邻域\(candidate(BACD)=\{ABCD,BCAD,BADC\}\),然后选择该邻域内代价最小的解\(ABCD\),其代价为10,所以不更新历史最优解。最后,更新禁忌表\(H=\{(BACD,1),(ABCD,2)\}\)。
类似地,不断迭代搜索最优解直到满足算法的终止条件,最终输出历史最优解。
实际上,在第二次迭代中\(BADC\)的代价也是10,具体要选择哪一个解,可以根据自己的倾向随机选一个即可。在这个示例过于特殊,因为初始解实际上就是一个最优解。如果不让初始解马上又被选中,可以在初始化的时候就把初始解加入到禁忌表中。
还需要注意的是:
(1)不要仅仅局限于将解作为禁忌对象,禁忌对象可以是其他任何合理的元素。例如,我们也可以将上述例子中代价值作为禁忌对象。此时,如果有一个解的代价值存在于禁忌表中,那么该解就不能被选中,这就强迫算法只能去选择具有不同代价的解。
(2)禁忌长度需要合理选择,禁忌长度太短容易陷入局部最优点,无法跳出;太长容易造成计算时间较大,更糟的情况是计算无法继续进行下去。一种策略是禁忌长度是一个可变的数,当禁忌表新加入一个禁忌对象时,就为其禁忌长度随机设置一个位于\([N_1,N_2]\)之间的整数值。
(3)在实际搜索中,可能出现所有候选解都处于禁止选中的状态,为了能够让算法能够正常继续下去,就需要引入特赦准则。特赦准则允许我们让禁忌表中代价最小(或某种指标最好)的对象能够被重新选中。从这个角度来看,这相当于加强了对某个较优局部的搜索,以希望发现更好的解。
终止条件:
- 设置最大迭代次数。
- 采用频率控制,当某个解、目标值或元素序列出现的频率高于给定的阈值,停止算法。
- 如果在给定的迭代次数内,历史最优值未发生变化,可以停止算法。
算法描述:
有了上述的讨论,禁忌搜索可以描述为
- 初始化一个初始解\(x_0\),禁忌表置为空集,记录历史最优解,以及其他所需的参数。
- 判断是否满足停止规则,如果不满足,那么就就从候选集\(candidate(x_0)\)中选取一个评价指标最优的解,作为当前解。然后更新禁忌表,重复执行第2步。
4.3 算法实现与测试
测试5城市非对称的TSP问题
代码实现:
import numpy as np
import operator
class Solution:
__slots__ = ('value', 'cost')
def __init__(self, value, cost):
self.value = value
self.cost = cost
class Item:
__slots__ = ('solution', 'nTimes')
def __init__(self, solution, nTimes):
self.solution = solution
self.nTimes = nTimes
class TS:
def __init__(self, nCities, nTimes, num_iter, dist):
self.nCities = nCities
self.nTimes = nTimes
self.num_iter = num_iter
self.dist = dist
self.best = None
self.table = []
def getRandomSolution(self):
temp = [i for i in range(self.nCities)]
np.random.shuffle(temp)
return Solution(temp, self.getCost(temp))
def getCost(self, x):
cost = 0
for i in range(self.nCities):
cost += self.dist[x[i], x[(i + 1) % self.nCities]]
return cost
def get_candidates(self, x):
cans = []
for i in range(self.nCities - 1):
temp = x.value[:]
temp[i], temp[i + 1] = temp[i + 1], temp[i]
cans.append(Solution(temp, self.getCost(temp)))
return cans
def update_table(self):
delete = []
for item in self.table:
item.nTimes -= 1
if item.nTimes == 0:
delete.append(item)
for item in delete:
self.table.remove(item)
def isAvailable(self, x):
for item in self.table:
if operator.eq(item.solution.value, x.value):
return False
return True
def solve(self):
# 初始化
x = self.getRandomSolution()
self.best = x
self.table.append(Item(x, self.nTimes))
# 开始搜索
for _ in range(self.num_iter):
self.update_table()
cans = self.get_candidates(x)
while cans:
x = min(cans, key=lambda s: s.cost)
if self.isAvailable(x):
self.table.append(Item(x, self.nTimes))
break
else:
cans.remove(x)
else:
# 特赦
x = min(self.table, key=lambda i: i.solution.cost).solution
if x.cost < self.best.cost:
self.best = x
return self.best
if __name__ == '__main__':
dist = np.array([
[0, 1, 5, 4, 3],
[3, 0, 2, 6, 1],
[5, 2, 0, 1, 4],
[1, 6, 3, 0, 3],
[3, 3, 1, 4, 0]
])
ts = TS(
nCities=5,
nTimes=3,
num_iter=10,
dist=dist
)
s = ts.solve()
print(s.value)
print(s.cost)
测试结果:

这里[0,1,4,2,3]表示访问城市的顺序为:0->1->4->2->3->0


 浙公网安备 33010602011771号
浙公网安备 33010602011771号